Research Article - (2022) Volume 11, Issue 3
Received: 11-May-2022, Manuscript No. JME-22-63581;
Editor assigned: 16-May-2022, Pre QC No. JME-22-63581(PQ);
Reviewed: 31-May-2022, QC No. JME-22-63581;
Revised: 11-Jul-2022, Manuscript No. JME-22-63581(R);
Published:
19-Jul-2022
, DOI: DOI: 10.37421/2169-0022.2022.11.22
Citation: Shukla, Shivangi, Shreyansh Jain and B.K. Behera. "Design and Development of 2D Woven Auxetic Fabric Based on Double Arrow Geometry using Semi-Empirical Model." J Material Sci Eng 11 (2022): 22.
Copyright: © 2022 Shukla S, et al. This is an open-access article distributed under the terms of the creative commons attribution license which permits unrestricted use,
distribution and reproduction in any medium, provided the original author and source are credited.ed.
Auxetic materials are materials that expand in the transverse direction when stretched longitudinally, giving them some unique properties in comparison to conventional materials. In textiles, both auxetic and non-auxetic yarns can be used to weave auxetic fabrics. This article demonstrates the modeling of a double arrow auxetic geometry for estimation of Poisson’s ratio and subsequent development of a woven construction to examine the potential of this geometry to produce an auxetic fabric. The fabric structure is modified to incorporate the double arrow auxetic geometry using a combination of loose and tight weaves, as well as elastic and inelastic yarns. The fabric structure is modeled semi-empirically. To determine the effect of yarn elasticity on the auxeticity of the fabric structure, three different counts of cotton spandex yarns were used. It was observed that when the different weft counts were used, the coarser weft count exhibited NPR over a wide strain range. The semi-empirical model of double arrow geometry fits the experimental data well.
Auxetic fabric • NPR • Double arrow geometry • Semi-empirical model
Auxetic materials are materials that have Zero Poisson's Ratio (ZPR) or a Negative Poisson’s Ratio (NPR) . When stretched longitudinally, these materials either extend or exhibit no deformation in the lateral direction, as illustrated in Figure 1. The auxetic material possesses extraordinary properties because of NPR, which makes it unique for certain applications. They have enhanced some properties like shear resistance, synclastic curvature, crashworthiness, sound absorption indentation resistance, vibration damping and energy absorbance and better formability. These properties make auxetic material different from conventional material. These properties can be exploited for many applications like biomedicine military use, protection, aerospace, and textiles. It can be used in fashion garments and shapewear as it can easily adjust according to the body movements, as a stretchable chest band carrier [8-12]. Auxetic fabric can be used to make children’s clothing, Maternity wears, etc (Figure 1).
Figure 1. Auxetic material showing NPR when a) stretched; b) compressed, Auxetic material showing ZPR when; c) stretched; d) compressed.
In recent years researchers have developed a lot of interest in auxetic materials. Much auxetic material has been discovered and made in the field of metals, ceramics, foams, textile fibers, yarns, fabrics, etc. The auxetic fabrics can be manufactured either by using auxetic yarns, or the conventional yarns using knitting, non-woven, and weaving technology [13-16]. Several wefts knitted, warp-knitted, non-woven, and woven structures have been made using auxetic geometries based on foldable geometry re-entrant hexagonal geometry, double arrow geometry, rotating rectangle geometry, etc. But these knitted and the non-woven auxetic fabric has certain drawbacks like they have a higher thickness, poor structural stability, low strength, and low modulus [17-23]. While the auxetic fabric made from weaving technology has a lower thickness and better formability.
Auxetic woven fabric can be manufactured by using two ways: 1) by using auxetic yarns and 2) by using a combination of loose and tight weaves with conventional yarns of varying elasticity. But the auxetic yarns can’t completely transfer the auxetic behavior in fabric because of the structural limitation. Therefore, the auxetic fabric made from conventional yarn not only provides better formability but also provides better shape fitting and comfort.
Since different applications require different NPR values, however, producing a fabric with different structural parameters to obtain different NPR values is a very time-consuming and laborious process. As a result, modeling is necessary to determine the construction parameters for various auxetic fabrics. Thus, we can forecast NPR values before production. Some semi-empirical modeling and analytical models have been developed, so the parameters affecting the NPR of geometry can be identified [24-26].
The difficulty in making a woven auxetic fabric is to realize auxetic geometries into woven fabric structure to obtain auxeticity. The auxetic effect is based on the principle of differential shrinkage, the fabric shrinks at different levels in different regions. This differential shrinkage is created with the help of elastic and non-elastic yarn along with a loose and tight weave. The elastic yarns give stretchability to stretch fabric while the non-elastic yarn gives firmness to the fabric. The differential shrinkage can be created in both weft and warp directions. As the fabric is released after weaving the loose weaves woven get shrunk while the tight weave will not shrink or will shrink a little. The high shrinkage of loose weave will make the tight weave collapse and will lead to the formation of folds that get unfolded when stretched and will show auxetic nature.
The challenge in manufacturing a woven auxetic fabric is incorporating auxetic geometries into the woven fabric structure to achieve auxeticity. The auxetic effect is based on the principle of differential shrinkage, in which the fabric shrinks at varying levels in various regions. Differential shrinkage is achieved using elastic and non-elastic yarns, as well as a loose and tight weave. Elastic yarns provide stretchability to a fabric, whereas non-elastic yarns provide firmness. Whereas when the fabric is released from the loom after weaving, the loose weaved region undergoes higher shrinkage as compared to the tightly weaved regions. Due to the high shrinkage of loose weave, the tight weave collapses, resulting in the formation of folds that unfold when stretched and exhibit auxetic nature. In this research, an effort is being made to model, develop, and characterize the Poisson’s ratio of 2D woven auxetic fabrics based on double arrow geometry.
Semi-empirical modeling of auxetic woven fabric based on double arrow geometry
Deformation mechanism of auxetic double arrow geometry: The unit cell of a double arrow geometry is considered as shown in Figure 2, where the initial parameter before stretch are: Length of the bigger arm is l, Length of the smaller arm is t, Angle between two arms of length l is α and angle between two arms of length t is β, whereas after stretch the parameter changes as Length of bigger arm changes to l’, length of smaller arm changes to t’, the angle between two arms of length l changes to α’ and angle between two arms of length t changes to β’. When double arrow geometry is stretched in the ydirection, the unit cell of the double arrow expands in the x-direction due to the opening of the angles between these two arms.
Figure 2. Change in the dimension of geometry before and after the stretch.
Therefore, expansion of the unit cell in both directions upon the action of force along the y-axis results in a negative Poisson’s ratio.
Development of semi-empirical equation: The unit cell of double arrow geometry as shown in Figure 1
In triangle ABC
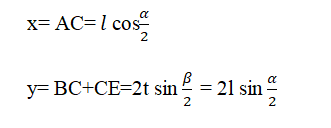
Length of the unit cell after the stretch
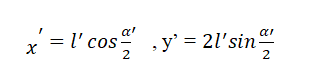
Calculation of axial strain
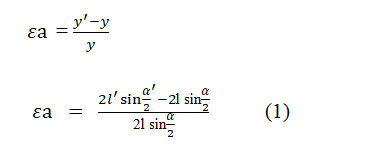
Finding the value of
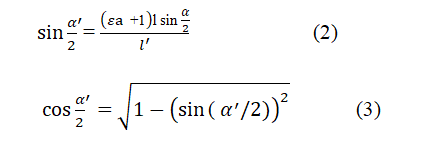
Calculation of transverse strain
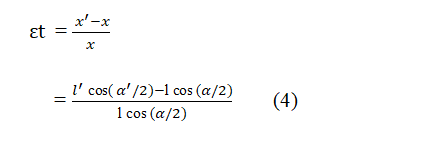
Substituting the value of in equation 4
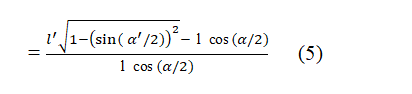
Putting the value of from equation 2
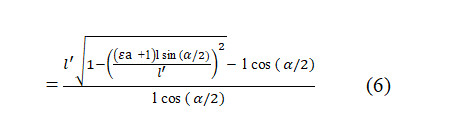
Calculation of Poisson’s ratio
For the calculation of Poisson’s ratio, equation 5 is divided by equation 1.
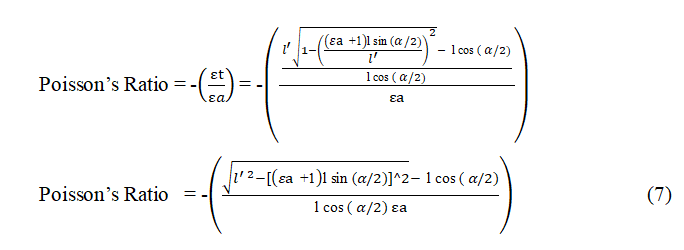
Materials
The construction of woven fabric involves two types of yarn, i.e., warp and weft. Here three different samples have been made by varying the weft yarn count. Therefore, the woven fabric is constructed by using 60/2 ss cotton in the warp direction and 60/2 s, the 20 s and 16 s cotton spandex in the weft direction for three different fabric samples. Sample coding is shown in Table 1.
| Sample codes | Yarn type |
|---|---|
| P | Cotton 60/2 ss |
| Q | Cotton Spandex 60/2 ss |
| R | Cotton Spandex 20 s |
| S | Cotton Spandex 16 s |
Design and development of auxetic woven fabric based on double arrow geometry
Arhane paint software is used to differentiate the geometry into distinct deformation zones. Using Arhane weave software, different weave designs are introduced into these various deformation zones. Five distinct zones of deformation have been identified, as illustrated in Figure 3, and the weave design of the unit cell is illustrated in Figure 4. The green portion is kept rigid so that it does not deform when a load is applied in the Y direction. Due to the requirement for arm openings of the double arrow geometry, the red and blue sections are woven more loosely than the purple and yellow sections. Plain weave is used to fill the rigid portion of the double arrow green region. The red section, blue, purple, and yellow sections have a 4/1 twill, a 1/4 twill, a 2/1 twill, and a 1/2 twill, respectively. Figure 3 illustrates the weave pattern for this geometry.
Figure 3. Unit cell of double arrow geometry along with deformation zones.
Figure 4. Weave design of double arrow.
For the development of the woven fabric, warping of the cotton 60/2 ss yarns was done, whereafter drawing and denting were done on Rapier CCI dobby loom, where 20 Heald shafts were used. And three different weft yarn counts were used for picking. The fabric construction parameters are shown in Table 2.
| Sample name | Warp | Weft | EPI | PPI |
|---|---|---|---|---|
| A | cotton 60/2 ss | 60/2 ss Cotton Spandex | 40 | 80 |
| B | cotton 60/2 ss | 20 s Cotton Spandex | 40 | 80 |
| C | cotton 60/2 ss | 16 s Cotton Spandex | 40 | 80 |
Characterization of yarn and fabric
Tensile test of the yarns: To determine the yarn properties, a tensile test was carried out using ASTM D2256 on an Instron tensile tester, where single-strand yarn specimens are broken on a tension testing machine at a predetermined elongation rate and the breaking force and the elongation at break are determined. The specimen length under test was kept at 250 mm and the test speed was 300 mm/min.
Image analysis of fabric: The visual analysis of the developed samples is done by looking at the appearance of the fabric, i.e., the appearance of the folds on the fabric surface and reduction in the width of the fabric after taking off the loom.
Determination of Poisson’s ratio of the fabric: To determine the Poisson’s ratio of the developed auxetic structures tensile testing was done using a video extensometer setup attached to Zwick Roell Z250 UTM machine. The testing was done in the weft direction due to the placement of elastic yarns as weft. Four points are marked on the fabric sample, to measure the change in length in the transverse and axial directions. Screenshots are taken at a regular interval from the video at different strain %. The values of strain in the axial and transverse directions are noted. The experimental setup is shown in Figure 5. Specimen of 5 cm x 20 cm was used. The jaw size used was 5 cmx5 cm and the speed during the test was 30 mm/min, with a gauge length of 10 cm. The fabric structure was analyzed with high accuracy at different strain levels using Digimizer image analysis software. The unit cell of double arrow geometry was marked and the change in length (l) was measured at different axial strain percentages, to find the regression between the change in length and axial stain%.
Figure 5. Experimental setup for video-extensometer.
Tensile properties of the yarns
The tensile behavior of the yarn P, Q, R, and S is shown in Figure 6-7. It is observed from the graphs that the yarn S shows maximum elongation followed by yarn R, Q, and P, due to the presence of spandex in the core of the yarn Q, R, and S. therefore, these elastic yarns (yarn Q, R,S) showed higher elongation compared to the inelastic yarn. Table 3 shows the breaking elongation and extension percentage at the break for the yarns used .
Figure 6. Tensile test of the yarns used.
Figure 7. Image analysis of fabric having different counts A) 60/2 ss; B) 20 s; C)16 s.
| S.No | Type of yarn | Breaking load (N) | Elongation at break (%) |
|---|---|---|---|
| P | Cotton 60/2 ss | 3.52 | 12 |
| Q | Cotton Spandex 60/2 ss | 3.63 | 36 |
| R | Cotton Spandex 20 s | 4.5 | 53 |
| S | Cotton Spandex 16 s | 4.53 | 93 |
Determination of auxeticity
The auxetic effect of the developed fabric samples is shown in Figure 8. It is observed that the woven fabric A made with 60/2 ss cotton spandex shows a maximum NPR of -0.11 at 1% axial strain and auxeticity can be obtained up to 15%. When 20 s cotton spandex weft in the fabric B is used, the maximum NPR of -0.27 at an axial strain of 1% and auxeticity can be obtained up to 26% axial strain, whereas, in the case of fabric C, 16 s cotton spandex is used, which shows maximum NPR of -0.41 at an axial strain of 1% and auxeticity can be obtained up to 42%. When the fabric is stretched along the weft, warp yarns get straight which were bent because of the differential shrinkage phenomenon. This straightening of warp yarns leads to an increase in the dimension of fabric in the warp direction. Therefore, NPR along stretched in weft direction is obtained. The summary of the results is shown in Table 4.
Figure 8. Comparison of NPR of the fabric of different weft count.
| S.No | Fabric sample | Maximum NPR | Corresponding axial strain % | Poisson’s ratio negative up to axial strain % | Average poisson’s ratio |
|---|---|---|---|---|---|
| 1 | Double arrow (2/60) | -0.11 | 1 | 15 | -0.05953 |
| 2 | Double arrow (20 s) | -0.27 | 1 | 26 | -0.03479 |
| 3 | Double arrow (16 s) | -0.41 | 1 | 39 | -0.03472 |
The maximum value of NPR was observed in all the three cases NPR, at initial strain rates. The fabric C shows maximum NPR followed by fabrics B and A up to 4% axial strain because of a greater number of folds and higher shrinkage. These folds get unfolded as the strain percentage increases. After 4% strain, fabric A shows higher NPR as compared to fabrics B and C, since fabric A is developed from 60/2 ss yarn count which is finer, so it has a lot more inter yarn spaces which allow greater yarn movement. The NPR reduces as the axial strain increases in all three cases. The PR is negative at small axial strain as the small arm of the double arrow is free to open due to the 4/1 twill weave below it but after some time the smaller arm can’t open furthermore due to restriction created by its nearby warp and weft.
Verification of the model: The initial parameter of the double arrow in fabric A i.e., the length of the arm (l) was 2.71 cm and the angle between two-arm (α) was 40ºC. The variation in the trend of as a function of axial strain is shown in Figure 9. The shows a linear trend with axial strain based on trend the relationship can be made between axial strain percentage and change in length of bigger sidearm after stretch.
Figure 9. a) Unit cell of double arrow geometry; b) Variation of l ' as a function of axial strain.
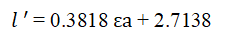
Putting the values of in equation 3
And the experimental and model PR are compared as shown in Figure 10.
Figure 10. Comparison of experimental and model results.
An auxetic geometry based on a double arrow structure was developed and analyzed. Auxeticity was successfully induced in woven fabric by visualizing double arrow geometry with the help of a commercial CAD system. As different weft counts were used it was found that the coarser weft count shows NPR over a larger strain range. The semi-empirical model of double arrow geometry shows good agreement with experimental results. The analysis reveals that this geometry can help to achieve different auxeticity in a woven construction.
The authors declare no conflict of interest.
Journal of Material Sciences & Engineering received 3677 citations as per Google Scholar report
