Research - (2023) Volume 11, Issue 4
Received: 12-Jul-2023, Manuscript No. jaat-23-105835;
Editor assigned: 14-Jul-2023, Pre QC No. P-105835;
Reviewed: 26-Jul-2023, QC No. Q-105835;
Revised: 31-Jul-2023, Manuscript No. R-105835;
Published:
07-Aug-2023
, DOI: 10.37421/2329-6542.2023.11.261
Citation: Nastasenko, Valentyn. “On the Need for Correction of Newton's Law of Universal Gravity within Classical Physics.” J Astrophys Aerospace Technol 11 (2023): 261.
Copyright: © 2023 Nastasenko V. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Newton's law of universal gravitation was discovered by him, perhaps in 1679, and published in 1687 in his paper “Principia”. At the beginning, he simply established a correspondence between the gravitational force F and the masses m1 and m2 of 2 point objects located at a distance r between them: F ~ m1m2/r2. However, this dependence is not a strict physical law, since the numerical value of the gravitational force found from it is not its real value. Therefore, instead of similarity, a transition coefficient should be introduced. It was first determined experimentally by Cavendish in 1798. Further, this coefficient was presented as the gravitational constant G. However, Cavendish did not connect G with Newton's dependence, but used it only to calculate the Earth's mass M within the framework of the GM combination. The constant G from this combination was identified by Jolly in 1878, which reduced Newton's original dependence to the real law of universal gravitation F=Gm1m2/r2, which is currently used. However, Newton got his dependence on the basis of the rotation of the Moon around the Earth, whose orbit is close to circular. Therefore, the radius r in it was taken constant. This law is being criticized because it does not operate at the planetary level, where the planets of the solar system do not move in a circular orbit, but, elliptical, within the framework of Kepler's laws. Eliminating the discrepancy between Newton's law of universal gravitation and Kepler's laws is the goal main of this work, and the formulation of a new corrected law is its scientific novelty. As a result of this work, it was proposed to replace the radius r with the current value ri in Newton's law, which can change according to its own laws. In this case, the new value of the law of universal gravitation has the form: F=Gm1m2/ri2. Unlike the original Newton's law, in which the radius r=const, in the corrected law ri=var, so the original law is a special case of the corrected law. In this case, the value of the radius ri2 can be obtained through the coordinate’s xi2, yi2 of the current points of the trajectory of the center of mass m2 of an object of smaller magnitude relative to the center of mass m1 of an object of larger magnitude. For an object with a spatial form of the trajectory of the center of mass, the 3rd coordinate zi2 is added to determine this radius. In its final form, the new law of universal gravitation will be expressed by the dependence: F=Gm1m2/(xi2+yi2+zi2). Thus, despite the criticism of Newton's law by opponents, he is acted, acts and will act in the material world. Conclusion, the Proposed revised law of universal gravitation are recommended for use in scientific research. This corrected version should be included in all textbooks and reference books on physics, incl. in the encyclopaedia.
Law of Universal Gravitation • Extension of its universality for non-circular orbits
The work relates to the field of gravity and gravitational fields, in particular - to Newton's law of universal gravitation and the action of the forces arising from his, within the framework principles of classical physics. In the context of ever-increasing need to expand scientific knowledge about the material world and the Universe, in the development of cosmology, astronautics and nuclear physics, deepening the understanding of the essence and all the features of the operation of Newton's law of universal gravitation is urgent task that is of great scientific and applied importance. This is explained by the fact that it is a global law of nature that operates at all levels of the material world, from elementary particles, atoms and molecules, to planetary and star systems, galaxies, meta galaxies and the Universe as a whole. Therefore, the works of many scientists of the world are devoted to its study. Without diminishing their importance, a full analysis of these works is beyond the scope of this study. Therefore, it was limited to work [1], in which there is a sufficient amount of information about Newton's law of universal gravitation.
Analysis of the state of the problem, the choice of goals and objectives of the study
It is currently accepted that the general theory of relativity (GR) developed by Einstein [2], in which the effects of gravity are replaced by the curvature of space-time, instead of the action of forces, has supplanted all other gravitational models, including Newton's laws. However, general theoretical principles adopted in GR and generalized approaches to building models with parameters from 0 to ∞, create a wide field for varying the initial and final results, which is shown in [3] using the examples of Figures 1 and 2 [4,5].
Figure 1.Mathematical models of the curvature of space in the area of the Earth and Moon [4].
Figure 2. The modern model of the curvature of space by the mass of Earth [5].
In the first case, the curvature of space is associated with the orbit of the Moon, and in the second case, with the closer orbit of the Earth's satellites. In this case, the parameters found from Newton's law are taken as the initial and comparative results of the simulation. Thus, the law of universal gravitation has not lost its significance and is currently used to calculate the motion of planets and other cosmic bodies of the solar system, incl. asteroids, comets and artificial satellites of the Earth, which confirms the need for its analysis. In addition to the indicated shortcomings (Figure 1 and 2), in the work [3] others are indicated, in particular, it is not clear how the space under and above the objects is formed.
The problem is also the direction of the deflection of space. On figure 1 and 2 it is directed downwards. This is the inertia of thinking, since the gravitational pull of the Earth is under our feet. However, within the framework of the principles of Einstein's theory of gravity, the curvature of space occurs in the direction of a massive object, which for the solar system is the Sun, which leads to a mismatch of the modeling planes [6]. Newton's theory of gravity does not have such problems; therefore it continues to be used. It should also be taken into account that general relativity and other branches of modern physics have not cancelled the laws of classical physics, which are set out in physical textbooks and reference books, which makes it possible to use and study them.
Newton's law of universal gravitation may have been discovered by him as early as 1679, and published in 1687 in Newton's “Principia” (Figure 3) [7].
Figure 3. Title page of Newton's scientific work “Mathematical Principles of Natural Philosophy” [7].
The source was a letter to Newton by Robert Hooke, in which he expressed his hypothesis about orbital motion, which partly depends on the strength of inverse squares [8]. On this basis, Newton first established that the gravitational force of 2 objects is inversely proportional to the square of the distance r2 between them, and then he established a correspondence between the gravitational forces F1=F2 and the masses m1 and m2 of two point objects (Figure 4), within the a priori dependence (1) [7]:
Figure 4. Gravitational interaction of 2-point physical bodies.
However, dependence (1) is not a strict physical law, since the numerical value of the gravitational force found from it does not correspond to its real value. Newton found only the proportionality of the forces F1=F2 to the masses m1 and m2 and the square of the distance r between two point objects. Therefore, instead of similarity (1), a transition coefficient should be introduced into the real law.
This coefficient, further represented as the gravitational constant G, was first experimentally determined by Henry Cavendish in 1798 [9]. To do this, he used a torsion balance built by the priest John Michell (Figure 5), which is similar to Coulomb's torsion balance. However, Michell may not have been aware of them. A simplified diagram of the contemporary torsion balance is shown in Figure 6 [10].
Figure 5. Model of the torsion balance Henry Cavendish, with which the gravitational attraction between laboratory bodies his first measured [Science Museum/Science & Society Picture Library].
Figure 6. Modern classical measurement scheme on the base of Cavendish-Michell torsion balance [10].
However, Cavendish did not connect the found coefficient with dependence (1), but used G only to calculate the mass M of the Earth [9] within the framework of the Gravitational Parameter [11], its GM combination. In terms of modern units of measurement SI, the value found by Cavendish is G=6.754 × 10-11 m3/(kg s2), however, different authors give different results of the measurement of G.
Separate from the combination GM constant G for systematic use, incl. in the depending (1), was introduced by Jolly on the basis of experiments in 1878 [12] (almost 80 years after the Cavendish experiments). In the works of Jolly, the value G=6.67 × 10-11 m3/(kg s2). Since that time, the law of universal gravitation has acquired its current form (2):
At present, the G value recommended by CODATA [13] is the numerical value (3):
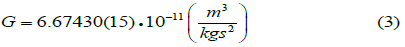
Thus, Jolly's error is only 0.65%, and over 145 years of research (1878 … 2023), its value G was refined only by 3 digits, of which the last digit have errors. In his work, Newton considered the gravity of the Earth and the Moon, which moved around the Earth in an orbit close to circular. Therefore, the radius r in dependences (1) and (2) was accepted by him as a constant value. In the twentieth century, the radius r began to be considered as a vector, but if we consider that the radius is the shortest distance between points, then there is no need for such a refinement.
However, the motion of the planets of the Solar System is not circular, but according to Kepler's laws [14], their orbits are elliptical. Therefore, in recent years, criticism of Newton's law of universal gravitation has intensified, as inaccurately reflecting the parameters of the material world. One of the biggest critics of this law is Abdul Malek [15]. The constancy of the radius r within the system of rotation of the Earth and the Moon may have been the product of the inertia of Newton's thinking, who did not analyze other options for the motion of the planets in the solar system and the principles of the operation of his law. Elimination of these shortcomings is the main goal of the work performed. Its scientific novelty is the expansion of the universality of the law of universal gravitation and its application to any kind of movement of gravitational masses.
Research methods
The work performed has a level of scientific discovery, for which the techniques have not yet been developed [16]. Therefore, it used the methods of the general principles of scientific research – deduction and induction, based on the application of the laws of dialectics [17], reliable laws of physics [18] and general ways of developing the theory of knowledge [19].
An analysis of the classical expression for Newton's law of universal gravitation (2) showed that it is very easy to eliminate its first drawback – the constancy of the radius r – if we replace r=const with the current value of the radius ri = var, which can change according to its own laws. In this case, the new value of the law of universal gravitation has the form (4):
Therefore, the original law (2) is a special case of the corrected law (4). Thus, despite the criticism of Newton's law by opponents regarding the nature of the movement of bodies, he acted acts and will act in the material world.
In the final form, the value of the radius ri2 can be obtained through the coordinate’s xi2, yi2of the current points of the trajectory of the center of mass m2 of an object of smaller magnitude relative to the center of mass m1 of an object of larger magnitude according to dependence (5)
Then, in the final version, the law of universal gravitation will have the form (6):
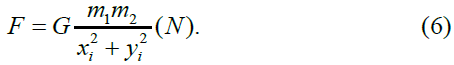
For example, in Kepler's laws [14], the orbits of the planets in the form of current points i on a simplified elliptical trajectory of their center of mass m2 relative to the Sun's center of mass m1, be obtained based on the scheme shown in Figure 7.
Figure 7. A simplified diagrams of the movement an elliptical orbit of the center mass of the planet, around of the center of mass of the Sun.
Here: A – Aphelion, P – perihelion, a – Semi-major axis of the ellipse, b – Semi-minor axis, F1 and F2 – foci of the ellipse, c – focal distance, p – focal parameter, rP – perifocal radius, rA – apofocal radius, i – the current point of the orbit, ri – the current radius, xi, yi – the coordinates of the current point of the orbit, υ1 – the orbital speed at aphelion, υ2– the orbital speed at perihelion.
The radius ri of the elliptical trajectory of motion and the coordinates xi, yi, at its current points i can be determined from dependencies (7), (8), (9):
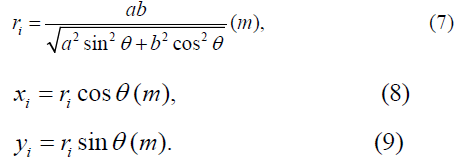
For the Earth and other planets of the Solar system, parameters ellipse has been determined as a result of astronomical observations. Parameters of orbit the Earth [20]:
- Aphelion A=152 098 232 km, perihelion P=147 098 290 km,
- Semi-major axis of the ellipse a=149 598 261 km,
- Semi-minor axis of the ellipse b=149 576 927 km,
- Orbital speed at aphelion υ1=30.27 km/s,
- Orbital speed at perihelion υ2=29.27 km/s.
Velocity values υ1 and υ2 provide connection with Kepler's 3rd law.
By changing the value of the independent angular parameter θ in the range from 0 to 2π, within the framework of dependences (7), it is possible to determine the current radius ri of the elliptical trajectory of the Earth's center of mass and its coordinates xi (8) and yi (9) at the current points. By substituting these values into dependences (4), (6), it is possible to determine the real values of the gravitational force during the motion of the Earth, and, by analogy, the forces for other physical objects for any trajectory of a flat type.
For objects with a spatial form of the trajectory of the center of mass m2, when determining the current radius ri2, the 3rd coordinate zi2 is added. In its final form, the new extended law of Universal gravitation will be expressed by dependence (10):
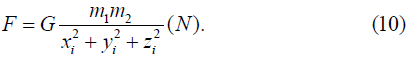
This principle is correct, since Newton's law of universal gravitation and all its constituent elements operate at all levels of the material world, from the initial quantum-mechanical level, with the Planck parameters of its constituent quantities [18], to the entire Universe.
New corrected versions (4), (6) and an extended version (10) of the law of universal gravitation should be introduced into all textbooks and reference books on physics, including in the encyclopaedia, because they have the level of scientific discoveries [21] and significantly deepen knowledge about the material world and its laws. Therefore, a discussion of the presented work is proposed, with recommendations for researchers and for CODATA.
New representations of the law of universal gravitation (6), (10) through the square values of the trajectory coordinates can make it possible to apply them to negative and imaginary numbers in the framework of dark matter and energy, but these are only mathematical transformations that have no real physical basis.
The main results of this work were presented at the World Conference on Physics and Mathematics (WCPM-Berlin-2023) May 22-23 and received approval [22].
1. Newton's law of universal gravitation in its modern form was formulated thanks to the works of Cavendish and Jolly, who determined the gravitational constant G for him.
2. The current formulation of the law of Universal gravitation makes it non universal, due to the constant value of the radius between interacting objects, which limits its strict application to objects with circular orbits, but solar system planets and many other objects, move along elliptical orbits and other curves.
3. To ensure the universality of Newton's law of universal gravitation, it is proposed to use the current value of the radius, which can change according to its own laws, both in the plane and in the volume of space. This makes the proposed law a new scientific discovery, which significantly affects the understanding of the laws of the material world.
4. To distinguish basic law of universal gravitation from the new one, it is proposed to add the names of "Newton's-Nastasenko" to its name, since the laws on scientific discoveries give the right to assign the name them of their authors.
5. The refined and expanded laws of universal gravitation are justified by strict physical dependencies and do not contradict the known laws of the material world. Therefore, they are recommended for use in scientific research and for study in the education system.
I am grateful to Abdul Malek for his criticism of Newton's law of universal gravitation. He allowed me to correct his mistakes and get a new, more accurate result.
The proposed work was carried out by the author independently as a personal initiative, based on personal scientific papers and literary sources open to the public. Permission to publish them is not required.
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Astrophysics & Aerospace Technology received 114 citations as per Google Scholar report
