Numerical Simulation of Influence of Pores Sizes on Water Migration Dynamic in Concrete Building Walls

Nde NM^1*, Fokwa D¹, Mbessa M², Tamo TT² and Pettang C^3
*Correspondence: Nde NM, Assistant Professor, Department of Civil Engineering, University of Douala, Douala, Cameroon, Tel: + 237695966339, Email:

Keywords

Mathematical modelling • Migration • Moisture • Numerical simulation • Pore size

Introduction

Construction materials are mostly parous media, and therefore subject to almost permanent moisture exchange with the environment around them. Among these construction materials, concrete is the most widely used in the world, and its water content due to its porous character, is an important parameter in terms durability of concrete structures. The influence of this porosity on the dynamics of moisture migration in concrete has been the subject of several publications. Thus, several authors have conducted research on the dynamics of water migration in concrete, going as far as modifying the porous structure of concrete thanks to various additives, in order to highlight the influence of these additives on the kinetics of migration and the moisture gradient in concrete. Ivan Lukic [1] shows that mineral additives increase the porosity of concrete, leading to high capillary absorption; Nilforoushan, and Reza [2] show that micro silica modifies pore size distribution and permeability of type V cement concrete; in fact, they show that the permeability of concrete with addition of micro silica decrease due to modification in pore size distribution. Similarly, Zineb Bajja [3] studied the microstructure of paste, mortars and concrete based on cement (CEM I), with silica addition, and shows that this addition modifies the microstructure and then influences the moisture transport properties. Moussa and others [4] show that the replacement of cement by iron powder improve the porosity and influence the water absorption of hardened concrete, especially the water absorption of the hardened concrete increase when the percent content of iron powder increase. Further on, Oltulu and Sahin [5], Mohseni and others [6] highlight the combined effects of nanoparticles: nano- SiO2, nano-Al2O3, nano- Fe2O3, nano- TiO2 powder on the water absorption dynamic. Djima and others [7] show the increasing of water absorption of concrete as the lime treated palm kernel shell and sugarcane bogasse ash increase in the concrete mixture. Malab and others [8] made comparative study of the drying kinetics of self-compacting concrete with those of an ordinary concrete and sand concrete, and show the first one with macropores has lower drying kinetics than the second with mesopores; these conclusions are also confirmed by Goual and others results [9], who show that the presence of macropores considerably attenuates moisture transport of civil engineering materials in general. Similarly, according to Suchorab and others [10], laboratory experiment and computer modeling confirm strong capillary properties of aerated concrete. Some authors have carried out research on the composition parameters of concrete and their influence on the porous structure and the moisture transport properties in concrete; thus Ghashghali and Hassani [11] show that characteristics such as water permeability and porosity present a clear dependence on the size of aggregate and mix design parameters; in fact the porosity and consequently water permeability coefficient decrease when the constant water to cement ratio (W/C) of pervious concrete increase. Suchorab [12] shows that the impregnation of building materials in hydrophobic solutions modifies their porosity leading to decreasing in dynamics of capillary moisture migration. However, even if these works take into account the porosity of materials, they do not explicitly highlight the pore size influence in the moisture migration; in other words, they studies carried out are sometimes contradictory and do not clearly present the role of pore size on the moisture migration dynamic in porous material. This work is part of the overall objective of highlighting the influence of pore sizes on the moisture migration dynamics specifically to show the influence of pore size on migration kinetics and moisture gradient in the wall. So, this paper first presents a mathematical modeling of moisture migration in a single layer wall; then, the results of numerical simulation are analyzed.

Material and Methods

To study the water migration in based of buildings, a mathematical model is proposed and then the numerical simulations are done with Matlab software. The method is based on finite differences and consists in defining an optimal geometry, space and time discretization, initial and boundary conditions.

Mathematical modelling

The model is based on the Philip and De Vries equations; moisture moves in the liquid and vapor state, with the moisture potential as the common potential. In this approach, the scale is assumed to be macroscopic, where the parous medium is considered to be an equivalent fictitious continuous medium; transfers are unsteady and one-dimensional; the different states (liquid and vapor) are in thermal equilibrium at any point in the parous medium; the capillary pores are assumed to be parallel and cylindrical. The liquid and vapor moisture flows are given according to Philip and De Vries [13] respectively by Equation (1) and Equation (2) while neglecting the gravity flow:

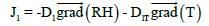(1)

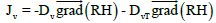(2)

J₁ and J_V represent the liquid and vapor moisture flow respectively, D₁ and D_V respectively the liquid and vapor moisture diffusion coefficients. D_1T and D_VT respectively the liquid and vapor moisture diffusion coefficients due to temperature gradient. T the temperature and RH moisture content (relative humidity).

At the liquid-gas thermodynamic equilibrium, Thomson’s equation [14] gives the relationship between relative humidity, temperature and pore radius as presented in Equation (3), and transformed to get Equation (4):

P_V/ P_0V= RH = esp [ (-2×T_s × γ_w cosβ) / (r×R×T) (3)

T = (-2×T_s ×λ_w ×cosβ) / (r×R×lnRH) (4)

P_V and P_0V are respectively the vapor pressure and the saturated vapor pressure; T_s the surface tension; YW the molar volume of water; r the pore radius; R the perfect gas constant and β the water contact angle.

A coupling of Equation (1), Equation (2), and Equation (4) lead to Equation 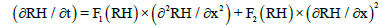(5):

(5)

With F1 (RH) and F2 (RH) the moisture migration coefficients, function of the moisture RH and given by the Equation (6) and Equation (7):

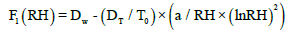(6)

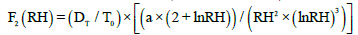(7)

Where a is a coefficient defined to simplify writing. DW the moisture diffusion coefficients due to water content gradient. And D_T the moisture diffusion coefficients due to temperature gradient [13].

a = (-2×T_s × γ_w ×cosβ) / (r×R) (8)

D_w = D₁ + D_v (9)

D_T = D_IT + D_VT (10)

Linearization

The computational of the homogeneous and nonlinear Equation (5) by the finite difference method requires to linearize it. An approximation is therefore made on the coefficients and, they are discrete and supposed known at time j and abscissa i. we then obtain Equation (11) and Equation (12):

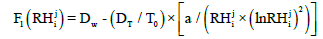(11)

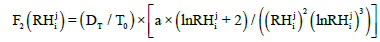(12)

Geometry and discretization

The diagram in Figure 1 illustrates the spatial and temporal discretization of the studied geometry.

The progressive finite differences method is used to discretize moisture flow, given by Equation (13); and the centered finite differences method discretize the moisture gradient, given by Equation (14)

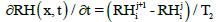(13)

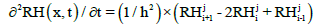(14)

With T2 and h respectively the temporal and spatial discretization rates, defined by Equations (15) and Equation (16):

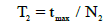(15)

h = e / N₁ (16)

e is the wall thickness, tmax the duration of moisture migration, N₁ and N₂ respectively the number of space and time steps.

Discrete formulation of the equation by Crank Nicolson scheme

For the discrete formulation of Equation (5), the second coefficient F₂ (θ) is excluded because its influence on the migration dynamics is negligible. Thus, the discrete scheme of Crank Nicolson, of Equation (17) leads to the algebraic equation system, Equation (18):

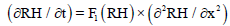(17)

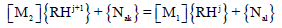(18)

[M₁] and [M₂] are the material characteristics matrix. The matrix of boundaries conditions are given at time j and j+1 respectively by {N_al} and {N_ak}

Initial and boundaries conditions, calculation parameters

The initial conditions and the boundaries conditions in moisture, applied to the geometry are defined as follows:

For x = 0, RH (0, t) = RH₀ (t) ∀t ≥ 0 (19)

For x = ∞, RH (∞, t) = RH₀ (t) ∀t ≥ 0 (20)

For t = 0, RH (x,0) = RH_i t = (0) ∀x (21)

The numerical values of the parameters used in this simulation come from Bordachev’s work on moisture calculation analysis and injection methods in brick masonry walls, where he shows that the revetment based on a material with high porosity or its injection into the wall basement, considerably limits the moisture migration in the wall [15]. Furthermore, some numerical values of parameters were taken from Kiwan’s work, on the reliability of energy performance in buildings [16]. Simulations are performed using Matlab software (version 7.10.0.499 (R2010a)), varying the pore size.

Conclusion

This paper presents a numerical simulation of moisture migration in concrete building walls, the influence of pore size on the dynamic of moisture migration has been highlighted, and it appears a low diffusivity in the center of the wall, this independently of pores sizes. Furthermore, a greater migration dynamic when the pores sizes decrease, means a greater kinetics of moisture migration and lower moisture gradient in the walls at the hygrometric equilibrium, for a decreasing pore size. These results find their applications in the choice of building materials their quality, their manufacture and their use for a better durability.

References

1. Lukic, Ivan, Vlastimir Radonjanin, Mirjana Malešev and Vesna bulatović. “Influence of mineral admixtures on water absorption of lightweight aggregate concrete” Scientific Conference, Planing, Design, Construction and Building Renewal (2015): 25-27.
2. Nilforoushan, Reza, M. “The effect of micro silica on permeability and chemical durability of concrete used in the corrosive environment” Iran J Chem and Chem Eng (2005).
3. Bajja, Zineb. “Influence de la microstructure sur le transport diffusif des pâtes, mortiers et béton à base de CEM I avec ajout de fumée de silice” Thèse de Doctorat, Université Paris -Saclay, Ecole normale Supérieure CACHAN 245: (2017).
4. Moussa, Anan Largeau, Raphael Mutuku and Joseph Thuo. “Effect of iron powder (Fe2O3) on strength workability, and porosity of the binary blended concrete” Open Journal of Civil Engineering, Scientific Research and Publishing 8 (2018): 411-425.
5. Oltulu, Meral and Remzi Sahin. “Effect of nano-SiO2, nano-Al2O3 and nano-Fe2O3 powder on compressive strength and capillary water absorption of cement mortar containing fly ash: comparative study” Energy and Building 58 (2013): 292-301.
6. Mohseni, Ehsan, Bahareh Mehdizadeh Miyandehi, JianYang and Mohammad Ali Yazdi. “Single and combined effects of nano- SiO2 , nano- Al2O3 and nano-TiO2 on the mechanical, rheological and durability properties of self-compacting mortar containing fly ash” Construction and Building Materials 84 (2015): 331-340.
7. Djima, Mahfouz OA, Geoffrey N Mang’uriu and John N Mwero. “Experimental investigation of lime treated palm kernel shell and sugarcane bagasse ash as partial replacement of coarse aggregate and cement respectively in concrete” Open Journal of Civil Engineering, Scientific Research and Publishing 8 (2018): 358-372.
8. Malab, S, Benaissa A, Boudraa S E and Aggoum S. “Drying kinetics of self-compacting concrete” Turkish Journal of Engineering and Environmental Science 33 (2009): 135-145.
9. Goual, MS, Bali A and Quéneudec M. “Influence de la structure poreuse sur le transfert d’humidité dans les matériaux poreux de génie civil ‘‘application au béton argileux cellulaire’’. Seminaire International de Géomatériaux GEOMAT’02, Université Mohamed Boudiaf de M’sila (2003).
10. Suchorab, Z, Widomski M, Łagód G and Sobczuk H. “Volatil organic compound protection against moisture in building materials” Ecological Chemistry and Engineering (2014):12.
11. Ghashghali, HT and Hassani A. “Investigating the relationship between porosity and permeability coefficient for pervious concrete pavement by statistical modeling” Material Sciences and Applications, Scientific Research and Publishing 7 (2016): 101-107.
12. Suchorab, Zbigniew, Widomski M, Lagod G and Sobczuk H. “Capillary rise phenomenon in aerated concrete" Monotoring and simulation (2010).
13. Philip, JR and De Vries DA. “Moisture movement in porous materials under temperature gradients” Transaction of American Geophysical Union 38 (1957): 222-232.
14. Thomson, W. “On the equilibrium of vapour at a curved surface of liquid” Philosophical Magazine 42 (1871): 448-452.
15. Bordachev, Alexander. “Moisture Calculation analysis and injection methods in brick masonry walls” Saimaa University of Applied Sciences (2010): 71p.
16. Lamis, K. “Fiabilité Des Performances Energétiques Des Bâtiments” (2012).
17. Abahri, K, Belarbi R and Trabelsi A. “Contribution to analytical and numerical study of combined heat and moisture transfers in porous building materials” Building and Environment 46 (2011): 1354-1360.
18. Fitsum, Tariku, Kumar Kumaran and Paul Fazio. “Transient model for coupled heat, air and moisture transfer through multilayered porous media” International Journal of Heat and Mass Transfer 53 (2010): 3035-3044.
19. Ketelaars, AAJ, L Pel, WJ Coumans, and PJAM Kerkhof. “Drying kinetics: a comparison of diffusion coefficients from moisture concentration profiles and drying curves”Chemical Engineering Science 50 (1995): 1187-1191.
20. Nytsch-Geusenet, Christoph, Thierry Nouidui, Andreas Holm and Wolfram Haupt. “A hygrothermal building model based on the object-oriented modeling language modelica” Building Simulation (2005).