Experimental Evidence for the Non-Zero Mass of Photons

Wim Vegt^*
*Correspondence: Wim Vegt, Department of Physics, Eindhoven University of Technology, Eindhoven, Netherlands, Email:

Keywords

Photons • Gravitational field • General relativity • Reflecting mirrors

Introduction

Imagine a thought experiment. A frictionless Scale has been placed witing a gravitational field. On each side of the scale has been placed a box with the inside covered with 100% reflecting mirrors. Both boxes are identically. One box remains empty. The other box has been filled with light (electromagnetic radiation). Because of the presence of the gravitational field (Gravitational Redshift), the frequency of the light will be a little lower at the top of the box and a little higher at the bottom of the box. Because of the proportionality of frequency and energy, also the radiation pressure at the top of the box will be a little lower than the radiation pressure at the bottom of the box. The scale will measure that the box filled with light is a little heavier than the empty box. The mass of the confined light (with electromagnetic energy W) equals according the well-known: W=m c2 (Equation 50). The confined light has mass and the rest mass of photons does not equal zero [1].

A fundamental aspect in Einstein’s Theory of General Relativity” is the concept that the rest mass of photons equals zero. This concept makes it impossible that photons interact with a gravitational field. Einstein has solved this problem with General Relativity which has been based on a curved Space-Time continuum.

Einstein has built his theory of General Relativity under the assumption of Maxwell that light has no inertia and that light does not generate its own gravitational field. For this reason Einstein had to develop a Curved 4-dimensional Space-Time continuum to explain the interaction between Gravity and Light. In this article a new theory has been presented that light (EMR) has its own inertia (term B1 in equation 27) and that light (EMR) generates its own gravitational field (term B6 in equation 27) which interacts with another gravitational field, causing the effects which have been described by General Relativity.

To test the new theory and compare the results with General Relativity, an accurate test has been required within a well-known gravitational field. This is the Test within the well-known gravitational field of the Earth: The Gravitational Redshift with Galileo Satellites in 2018 [1].

Materials and Methods

“Gravitational RedShift” due to the gravitational field of the Earth between an observatory on Earth (Radius= 6 10⁶ [m]) and a Satellite in a Galileo Orbit (R_adius=23222 10³ [m]) according “General Relativity”:

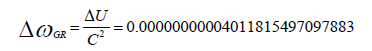
“Gravitational RedShift” due to the gravitational field of the Earth between an observatory on Earth (Radius= 6 10⁶ [m]) and a Satellite in a Galileo Orbit (R_adius=23222 10³ [m]) according “Quantum Light Theory”:

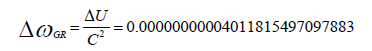
The difference between the calculation for Gravitational RedShift, within the Gravitational Field of the Earth, in “General Relativity” and “Quantum Light Theory” is smaller than 10^-16. Validation of both theories requires a sensitive and accurate observatory like the JWST or the SKA with observation accuracies smaller than10^-16

The principle of “Universal Equilibrium” to electrodynamics and electromagnetic interaction

Newton introduced in physics the concept of “Universal Equilibrium”, which he formulated in his famous third equation Action= - Reaction. (Newton’s third law) In nowadays math the concept of “Universal Equilibrium” has been formulated as:

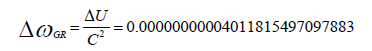
Because the Inertia Force is a Reaction Force, the Inertia Force appears in the equation with a minus sign (Newton’s second law).

Equation (2) is a general presentation of Newton’s famous second law of motion. In a fundamental way, Newton’s second law of motion describes the required electromagnetic equation for the Gravitational-Electromagnetic Interaction in general terms, including Maxwell’s theory of Electrodynamics published in 1865 [2] and Einstein’s theory of General Relativity published in 1911 [3]. To realize this new “Gravitational-Electromagnetic Equation”, the fundamental principle of equilibrium has been divided into 5 separate terms, as described by equation (3). Each one describes a part of the electromagnetic and inertia interaction force densities.

The first term B1 represents the inertia of the energy (mass-) density, the terms B2 and B3 represent the electric force densities, and the terms B4 and B5 represent the magnetic force densities, of electromagnetic radiation. Fundamentally, the outcome of (3) recalls the fundamental principle of “Universal Equilibrium”.

To apply the concept of universal equilibrium within an electromagnetic field, the electric forces F_i ^Electric the magnetic forces F_j ^Magnetic and the inertia forces will be presented separately in equation Fout! Verwijzingsbron niet gevonden.):

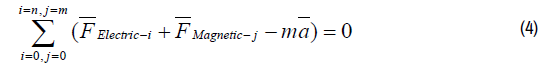
The first term (The Inertia of Light)

Albert Einstein’s “General Relativity” describes the interaction between “Gravity and Light”. It is impossible to build a framework for the interaction between Gravity and Light without describing the Inertia (mass) of Light. Because there can only be interaction between Gravity and Inertia (Mass). Without Inertia (Mass) there will be no interaction with gravity. The inertia (mass) of light is very different than the mass of objects we usually describe. The inertia (mass) of objects is always omni-directional. It does not matter in what position we put a mass on a scale, the weight (interaction) between gravity and the object will always be the same. Reducing Equation (2) to one single Force F , equation (2) will be written in the well-known presentation:

The right and the left term of Newton’s law of motion in equation (5) has to be divided by the Volume “V” to find an equation for the force density F related to the mass density “ρ”.

The Inertia Force F_Inertia for Electromagnetic Radiation will be derived from Newton’s second law of motion, using the relationship between the momentum vectors P for radiation expressed by the Poynting vector S :

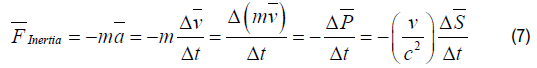
Dividing the right and the left term in equation (7) by the volume V results in the inertia force density f_Inertia :

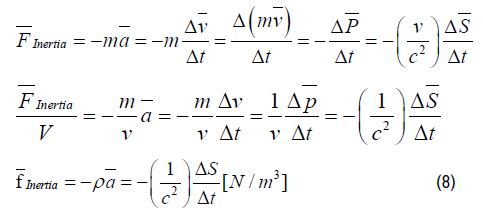
The Poynting vector S represents the total energy transport of the electromagnetic radiation per unit surface per unit time [J / m² s], which can be written as the cross product of the Electric Field intensity E and the magnetic Field intensity H .

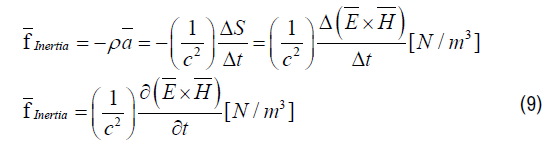
Second and fourth term in “Quantum Light Theory” (Term B-2 and B-4)

An example of the Coulomb Force is the Electric Force F_Coulomb acting on an electric charge Q placed in an electric field E. The equation for the Coulomb Force equals:

Dividing the right and the left term in equation (10) by the volume V results in the Electric force density f _Coulomb:

Substituting Gauss’s law in differential form in (11) results in Coulombs Law for Electromagnetic Radiation for the Electric force density f_Coulomb :

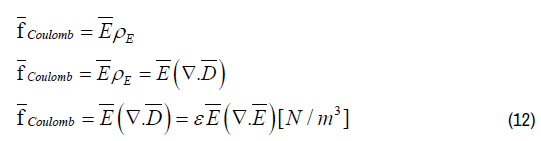
In Electromagnetic Field Configurations, there is in general no preference for the electric force densities or the magnetic force densities. In general the equations for the electric field densities are universally exchangeable with the magnetic field densities.

For the magnetic field densities, equation (12) can be written as:

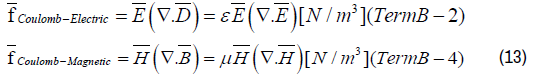
Third and fifth term in “Quantum Light Theory” (Term B-3 and B-5)

An example of the Lorentz Force is the Magnetic Force F Lorentz acting on an electric charge Q moving with a velocity v within a magnetic field with magnetic field intensity B (magnetic induction) (Figure 1).

The equation for the Lorentz Force equals:

Dividing the right and the left term in equation (14) by the volume V results in the Lorentz force density f_LORENTZ :

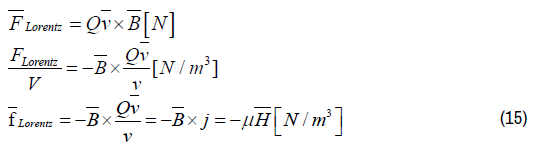
In which q is the electric charge, v the velocity of the electric charge, B the magnetic induction and j the electric current density. Substituting Ampère’s law in differential form in (15) results in Lorentz’s Law for Electromagnetic Radiation for the Electric force density f_LORENTZ

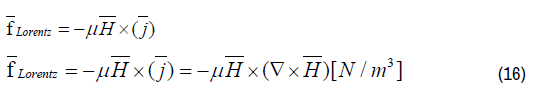
In Electromagnetic Field Configurations, there is in general no preference for the electric force densities or the magnetic force densities. In general the equations for the electric field densities are universally exchangeable with the magnetic field densities. For the electric field densities, equation (16) can be written as:

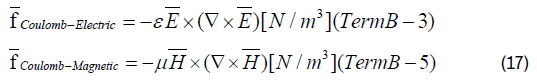
Fundamental equation for electromagnetic interaction in “Quantum Light Theory” (Term B-1+Term B-2+Term B- 3+Term B-4+Term B-5)

Newton’s second law of motion applied within any arbitrary electromagnetic field configuration results in the fundamental equation (23) for any arbitrary electromagnetic field configuration (a beam of light):

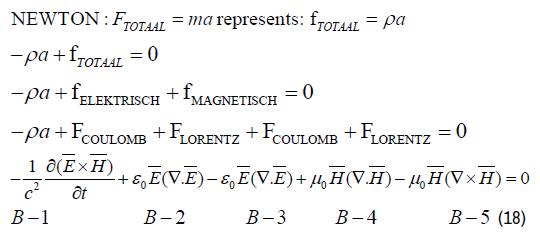
Term B-4 is the magnetic equivalent of the (electric) Coulomb’s law B-2 and Term B-3 is the electric equivalent of the (magnetic) Lorentz’s law B-5.

The Universal Equation for the Electromagnetic Interaction for Propagating Electromagnetic Waves (Laser Beam) and Confined Electromagnetic Waves (GEONs) has been presented in (19) and expresses the perfect equilibrium between the inertia forces (B-1), the electric forces (B-2 and B-3) and the magnetic forces (B-4 and B-5) in any arbitrary electromagnetic field configuration.

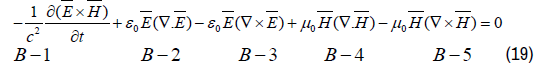
The integration of Maxwell’s Theory of electrodynamics in “Quantum Light Theory”

The “Fundamental Equation for Electromagnetic Interaction” (19) for any arbitrary electromagnetic field configuration can be written in the form:

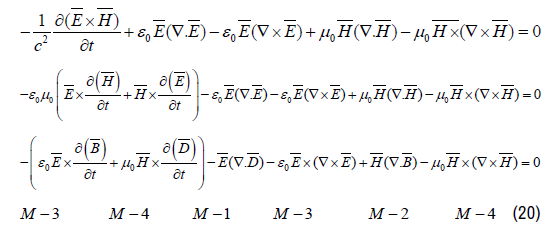
The Maxwell Equations are presented in (21):

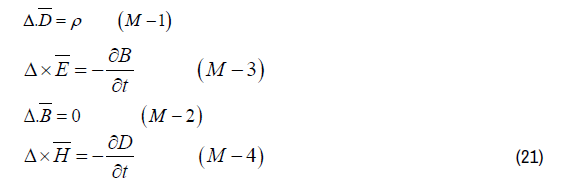
In vacuum in the absence of any electric or magnetic charge density, it follows from (21) that all the solutions for the Maxwell’s Equations (21) are also solutions for the “Fundamental Equation for Electromagnetic Interaction” (20) for the Electromagnetic Field.

Fundamental Equation for Electromagnetic Interaction

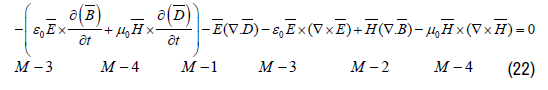
4 Maxwell's Equations

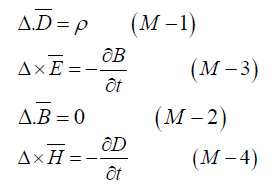
Comparing the 4 Maxwell Equations (21) with the “Fundamental Equation for Electromagnetic Interaction” (20) results in the conclusion that the 4 Maxwell equations show only the 4 parts of the “Fundamental Equation for Electromagnetic Interaction” in 4 separate terms and the 4 Maxwell equations are missing the fundamental term for inertia. For that reason it is impossible to calculate the interaction between light and gravity with the 4 Maxwell equations. To find the interaction terms between light and gravity the inertia term B-1 in (19) is necessary.

To define the “Fundamental Equation for Electromagnetic Gravitational Interaction”, an extra term (B-6) has been introduced in equation (27). The term B-6 represents the force density of the gravitational field acting on the electromagnetic mass density.

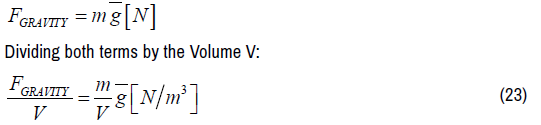
Results in the force density

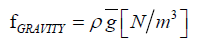
The specific mass “ρ” of a beam of light follows from Einstein’s equation:

W = mc²

Divinding both terms by the Volume V results in:

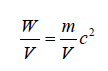
Which represents the energy density "w" and the specific mass " " of the electromagnetic radiation:(24)

W = ρc²

Which results for an ex expression of the specific mass P:

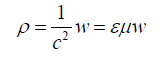
The energy density “w” follows from the electric and the magnetic field intensities:

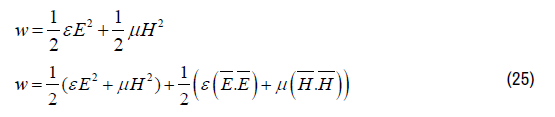
Substituting equation (53) in equation (52) results in the gravitational force density f_GRAVITY acting on an arbitrary electromagnetic field configuration (a beam of light) with mass density ρ.^

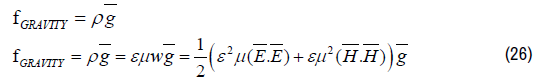
Substituting equation (25) in equation (26) results in the fundamental equation describing the Electromagnetic-Gravitational interaction for any arbitrary electromagnetic field configuration (a beam of light):

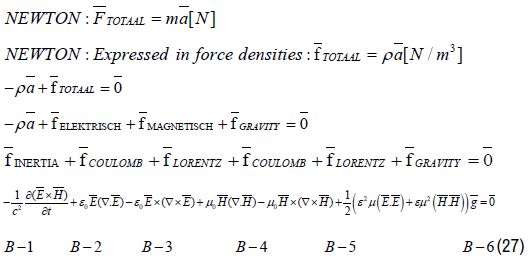
Term B-1 represents the inertia term of the electromagnetic radiation. Term B-4 is the magnetic representation of the (electric) Coulomb’s Force B-2 and Term B-3 is the electric representation of the (magnetic) Lorentz Force B-5. Term B-6 represents the Electromagnetic-Gravitational interaction of a gravitational field with field acceleration g acting on an arbitrary electromagnetic field configuration (a beam of light) with specific mass ρ.

The universal equation for the electromagnetic field (free electromagnetic waves and confined electromagnetic fields) within a gravitational field with gravity field intensity g has been presented in (48) and expresses the perfect equilibrium between the inertia forces (B-1), the electric forces (B-2 and B-3), the magnetic forces (B-4 and B-5) and the gravitational force (B- 6) in any arbitrary electromagnetic field configuration.

Discussion

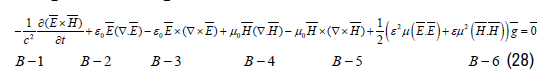
Planck’s constant in “Quantum Light Theory”

The fundamental relationship in the interaction between gravity and light is the proportionality between energy and frequency. This effect becomes measurable in “Gravitational Red/Blue-Shift.

To describe the “proportionality between Energy and Frequency (Planck’s Constant) for confined Electromagnetic Waves, an example has been chosen of an electromagnetic wave (light) confined between two 100% reflecting mirrors (Figure 2).

Figure 2 represents confined electromagnetic radiation with amplitude E0 and frequency ω₀. A general property of confined electromagnetic waves is the proportionality between energy and frequency. As an example the confinement of light between two perfect reflecting mirrors with surface A has been chosen. When both mirrors are being moved towards together over a distance Δx, the work ΔW has been delivered:

In which “A” equals the surface of the mirrors and “p” equals the radiation pressure:

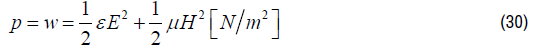
The Electromagnetic “Work ΔW” which has been delivered equals:

When over a time “Δt”one mirror move towards the other with a velocity “v”, then the distance “Δx” passed over a time interval Δt equals:

Substituting (29) in (30) results in:

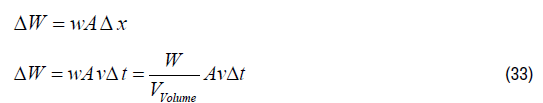
In which “W” equals the total energy involved in the transformation of Mechanical Energy into the Electromagnetic Energy.

When an observer moves slowly (not at a relativistic speed) towards a beam of light, a Doppler frequency shift appears:

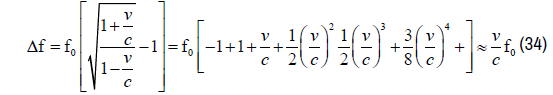
The same happens for the moving mirror. A shifted frequency will be reflected. The total effect of the displacement of the distance Δx will be a frequency shift in the confined electromagnetic radiation which equals:

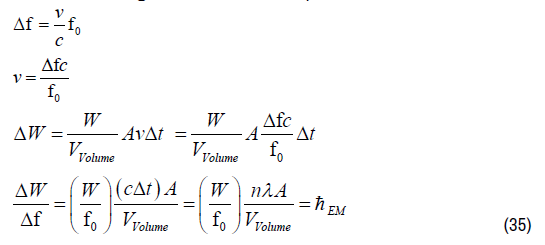
In which represents the wavelength of the confined radiation and “n” the number of wavelengths of compressions. The term h_EM represents an Electromagnetic equivalent for Planck’s constant.

“Gravitational RedShift/BlueShift due to “Electromagnetic Gravitational Interaction” in “Quantum Light Theory”

The “Universal Equilibrium Equation for Electromagnetic Waves interacting with a Gravitational Field with acceleration g has been presented in Equation (29)

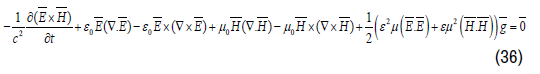
A fundamental Solution for Equation (64) within a gravitational constant gravitational field g in the z-direction, equals for the electric field [4].

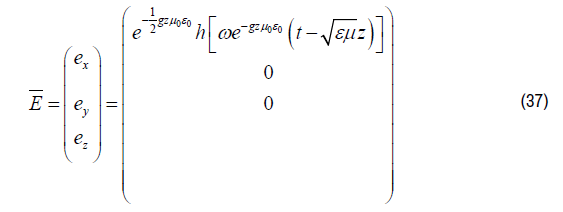
And for the Magnetic Field:

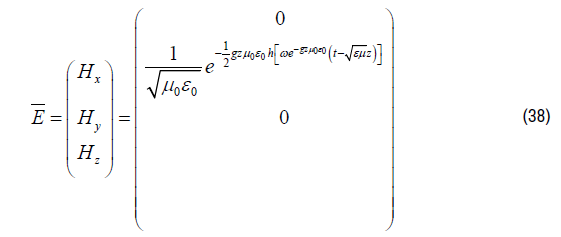
The term h_EM (Electromagnetic equivalent for Planck’s constant) defines proportionality between the energy density and the frequency ω. The solutions (37)) and (38) represent a “Constant Speed of Light” “c”. The “Gravitational Red- Shift” equals:

In which ω₀ equals the original frequency of the beam of light propagating in the direction of the constant gravitational field in the z-direction and the exponential term demonstrates the Gravitational Redshift when the beam of light moves away from the Gravity Source (Solar System or Black Hole). Including the “Doppler RedShift the total frequency shift equals:

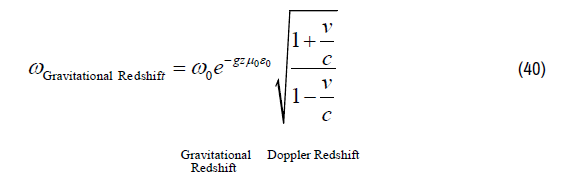
Equation (40) represents the “Gravitational Redshift” for a Constant Gravitational Field (with a constant gravitational acceleration “g”). The “Electromagnetic Equilibrium Equation” (27) in “Quantum Light Theory” represents possible solutions for all “Time- and Space Depending Gravitational Fields” and Equation (27) is the fundamental equation to be “tested” relative to Einstein’s theory of General Relativity. Measurements of “Gravitational Red-Shift/ Blue-Shift from World Wide Observatories could falsify or confirm this “Quantum Light Theory.”

For simplicity 3 distinguishments have been made for the different kinds of gravitational fields. The first one is a function with a linear increment to the source of the gravitational field (The center of the of the Milky Way Galaxy to the Edge of the Milky Way Galaxy) in which the gravitational acceleration “g” and the corresponding solution for equation (27) have been presents in equation (41-a). The second gravitational field is proportional to 1 / r2 (The gravitational field around the edge of the Milky Way Galaxy) in which “r” equals the distance. The third type of Gravitational Field is a constant Gravitational Field over Long Distances far away from sources of gravity like Black Holes.

Mathematical calculations for Gravitational RedShift/ BlueShift

When on Earth a ball has been thrown up, the Kinetic Energy (EM field) has been converted into a Potential Energy and the kinetic energy becomes smaller. When a Beam of Light (e.g. Laser Beam) shines up, something comparable happens. The EM Field Intensity becomes exponentially lower (the higher the beam shines upwards) but the speed of light does not change. The speed of light remains constant. For a Laser Beam shining downwards on earth, the opposite happens. The intensity becomes (exponentially) higher and the observed frequency higher (Blue Shift).

Equation (41) represents 3 solutions for 3 different kinds of Gravitational Fields:

The Gravitational RedShift (GRS) term in Quantum Light Theory (QLT) depends on the type of Gravitational Field:

ω_RS =ω_GRS ω_Doppler

Gravitational field type 1:

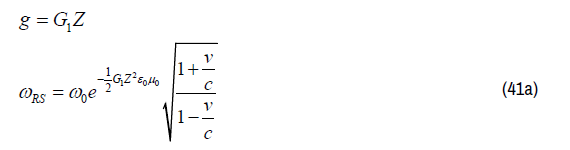
Gravitational field type 2:

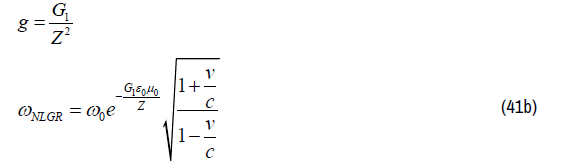
Gravitational field type 3:

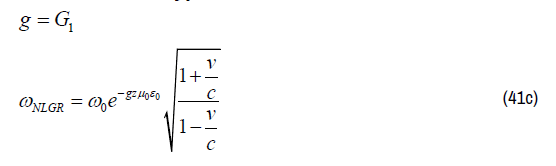
The Mathematical Solutions for the Gravitational Redshift term in Quantum Light Theory (GR_QLT) differ from the Gravitational Redshift in General Relativity (GR_GR) with a factor a. Within a constant gravitational field over a distance of 36000 [km] (average Satellite height) and an estimated gravitational acceleration of g= 9.8 [m s^-2].

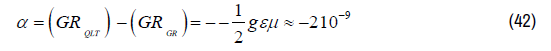
The Mathematical Solutions (41-b) for equation (27) have been calculated in [5].

The mathematical solutions for a gravitational field proportional to zn, the mathematical solutions for Equation (27) can be presented as:

Gravitational field type zⁿ

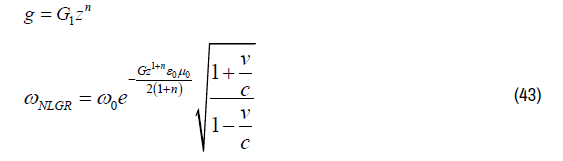
In general the mathematical solutions for Equation (56) can be represented as:

Gravitational Field as a function "h (z)" along the z- axis along the between "object" and "observer"

g = G₁g[Z]

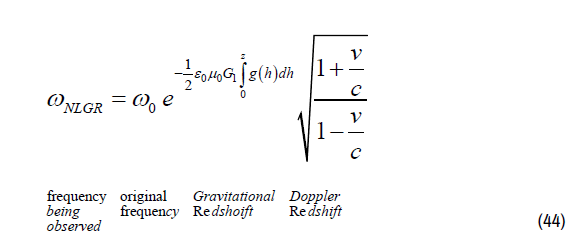
The mass (weight) of photons within a gravitational field defined by Gravitational Redshift

In physics the quantization of light has always been related to the quantization of Einstein’s concept of photons. In “Quantum Light Theory” the quantization of light has been related to a much broader concept also including Wheeler’s concept of GEONs [6].

It follows from equation 69-c (measured at velocity v= 0) that “Gravitational Redshift is responsible for the weight of photons in a gravitational field.

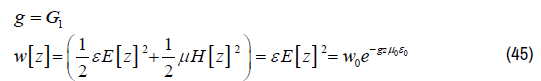
The radiation pressure on one side of the mirror equals:

De radiation pressure is on both mirrors oppositely directed. During measuring the weight of the confined radiation between both mirrors the difference in radiation pressure on both mirrors equals:

The resulting force on the system of 2 mirrors (1-dimensional confinement of Electromagnetic Radiation in the z-direction) with distance z and surface A equals:

Series Development of the exponential function results in:

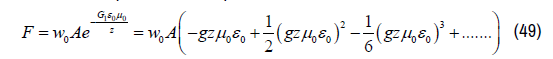
The resulting force on both mirrors with confined electromagnetic radiation with total EM energy W equals in first order approximation:

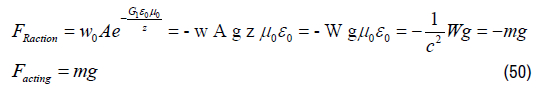
Due to the effect of gravitational Redshift, the resulting radiation pressure on confined electromagnetic radiation within a gravitational field is oppositely directed to the gravitational field and according Newton’s second law, the weight of the confined radiation equals the conventional mass for confined energy:

Conclusion

Einstein’s theory of “General Relativity” states that clocks at different gravitational potentials tick at different rates, relative to lab coordinates (an effect known as the Gravitational Redshift).

“General Relativity” and “Quantum Light Theory” are two fundamentally different theories calculating the interaction between Gravity and Light.

“General Relativity” has been based on a 4-dimensional curvature in Space and Time due to a Gravitational Field and light follows the 4-dimensional curvatures in Space and Time.

An accurate way to test both theories is the “Gravitational RedShift” within a well-known gravitational field like the gravitational field of the Earth. Both theories give different outcomes in the values for the “Gravitational RedShift” within the gravitational field of the Earth between an observatory on Earth (Radius=6 106 [m]) and a Satellite in a Galileo Orbit (Radius=23 222 106 [m]). The Galileo Space Segment comprises a constellation of a total of 30 Medium Earth Orbit (MEO) satellites, of which 3 are spares, in a so-called Walker 27/3/1 constellation.

“Gravitational RedShift” between an observatory on Earth (Radius=6 10⁶ [m]) and a Satellite in a Galileo Orbit (R _adius =23222 10³ [m]) according “General Relativity”.

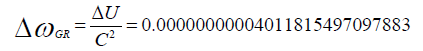
“Gravitational RedShift” between an observatory on Earth (Radius=6 10⁶ [m]) and a Satellite in a Galileo Orbit (R_adius=23222 10³ [m]) according “Quantum Light Theory”:

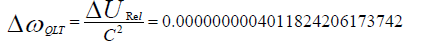
The difference between the calculation for Gravitational RedShift, within the Gravitational Field of the Earth, in “General Relativity” and “Quantum Light Theory” is smaller than 10-15. Validation of one of both theories requires a very sensitive and accurate observatory like the JWST or the SKA.

Data Availability

All the Data and all the Calculations to provide evidence to “Quantum Light Theory” have been published at:

https://quantumlight.science/

References

1. Herrmann, Sven, Felix Finke, Martin Lülf and Olga Kichakova, et al. "Test of the gravitational redshift with Galileo satellites in an eccentric orbit." Phys Rev Lett 121 (2018): 231102.

Google Scholar, Crossref, Indexed at

2. Maxwell, James Clerk. "VIII. A dynamical theory of the electromagnetic field." Philos Trans R Soc 155 (1865): 459-512.

Google Scholar, Crossref

3. Einstein, Albert. "On the influence of gravitation on the propagation of light." Annalen der Physik 35 (1911): 906.

Google Scholar, Indexed at

4. Vegt, Wim. "Propagation of light within a gravitational field in quantum light theory." Calculation in Mathematica.
5. Vegt, Wim. "Gravitational redshift between two atomic clocks." Calculations in Mathematica.
6. Wheeler, John Archibald. "Geons." Phys Rev 97 (1955): 511.

Google Scholar, Crossref, Indexed at