Sarkar Singularity in Gravitational Cosmology

Najmuj Sahadat Sarkar^*
*Correspondence: Najmuj Sahadat Sarkar, Department of Physics, Mahishadal Raj College, West Bengal, India, Tel: 6295454694, Email:

Keywords

Raychowdhury equation • Universe • Hubble construction rate • Time • Singularity • Penrose Diagram • Collapse

Introduction

From Einstein's equation, we know that our universe is expanding. Indian physicist Amal Kumar Raychoudhury gave a solution to Einstein's equation, which is known as Raychoudhury equation. The equation is in the following form:

Here, 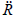= acceleration of the universe. R is system physical distance. G stands for the gravitational constant. ρ refers to the density of matter present in the system. p refers to the positive pressure of the substance present in the system. Now let's talk about what equation (1) actually means. The R/R term on the left represents acceleration. But the term on the right indicates something else. If both p and ρ are positive, i.e. greater than zero, then the value of (ρ+3p) will be much greater than zero. But according to the righthand side of equation (1) (ρ+3p) outside this term has negative sign. So [− (ρ+3p)] this total term will be less than zero. But R/R means Acceleration. R/R are not negative in general. So the entire term on the right-hand side represents attenuation. That is, if a system is considered, it cannot be stable. Due to increase in P and ρ, that means the system will start to compress or collapse [1]. The reason is also quite clear that increasing P and ρ means that the system will contract, which is what the Raychowdhury equation says. Take any system where matter is acting. Now positive gravitational pressure will act in the system in the presence of matter. After that the system starts to collapse due to presence of matter and squeezing into smaller and smaller volume. That is called Singularity we can easily analyze it from Pennors diagram. This is the key point of the Ray Chowdhury equation.

Description

The equation says exactly the same thing. Although the equation I tried to explain is a different analogy, which analyses the singular state. Here I have used H and t. I got the idea from my paper "A Mathematical proof of the big crunch" (Journal of Physics and Astronomy, Vol 11/Issue 6). There was a term, which went something like this-

Ṙ= -3ηt² × R Equation (2)

This means V=Ṙ=dR/dt. which is working as Hubble Velocity. As mentioned earlier, R is the physical distance of the system. t is the evolving time of the system. And η is a constant. Equation (2) looks a lot like V=HR or Hubble Law where

H= -3ηt² Equation (3)

Derivative of equation (2) with respect to t;

R= dṘ/dt= -[6ηtR+3ηt²Ṙ] Equation (4)

On the right side of equation (4) we get R, Common. dṘ/dt=-R[6ηt+3ηt²Ṙ/R]

Or,

1/R(dṘ/dt)= -[6ηt+3ηt²H] Equation (5)

Another thing, H= -3ηt² Or, H²=9η²t⁴

Or, H= ±3ηt²

But I am willing to work with positive values of H. Now substituting the value of H instead of 3ηt² in equation (5) we get-

(1/R) (dṘ/dt)= (6ηt+H²)

Equation (6) produces a singular situation. how? First, the term on the left side of equation (6) refers to acceleration [2]. That is, I am talking about the term R/R. Now come to the term on the right. Since; -

t>0 H>0

So (6ηt+H²)>0 will be.

But (6ηt+H²) has negative sign before this term. That is, − (6ηt+H²), so the entire term will have a large negative value. As H and t increase, the term on the right-hand side will have a large negative value. But the acceleration term is not negative. This means that the system we consider is decelerating. That is, the system is generally not stable. Due to deceleration, the system will eventually form a singularity before contracting. In a way, H will act as the Construction Rate in the far future. I think H and t their direction is always one way [3]. But currently no singular situation is emerging. There is still time for that to happen. My equation is not a special equation. This is a variant of the Raychowdhury equation. Only I am giving more importance to H and T here. In short, matter can indirectly affect the rate of expansion of a system. Since the Hubble Expansion Rate will act as the Contraction Rate in the distant future, we can expect a Possible Big Crunch. As said earlier H<0 cannot be. A long time ago we got a singularity, just like that i think we will get it in the future and this cycle will continue forever. Let's see if my equation is Dimensionally Consistent. First we apply [η] to get the units of η. Here H=3ηt² is a number of 3, which is not so important to us. Then we can say;-

[H]=[η][t]²

Or, [η] = [H]/[t]²

Or, [η]= km/s³/Mpc

The units of the terms on the right-hand side of equation (6) will be,

[η][t]+[H]²= km/s²/Mpc+km²/s²/Mpc²

= (km/s²/Mpc)(1+km/Mpc)

= (km/s²/Mpc)(Mpc+km)/Mpc

Now we can apply a convention. 1Mpc>>1km

From here it can be said, (km/s²/Mpc)(Mpc/Mpc) = km/s²/Mpc

Now let's consider the term on the left side i.e. R/R.

[R]= [dv/dt]= km/s² Again, [R]= Mpc So,

[R]/[R]= km/s²/Mpc

That is, the unit on the right side and the unit on the left side are equal to each other. My equation is completely Dimensionally Consistent [4]. Now I want to find the value of η at H=3ηt². First, the current value of H= 70 km/s/ Mpc and the current value of t, t= 5 × 10¹⁷s. So;-

H=3ηt²

Or, η= H/3t²

Or, η= 70/(75 × 10³⁴)

Or, η= 9 × 10^⁻35 Km/s³/Mpc

In this case η is a constant, whose value is very close to zero (Figure 1).

Conclusion

My equation is also a 2^nd order differential equation like Prof. Raychowdhury's. And just as his equation had a negative sign on the righthand side, my equation has a negative sign on the right-hand side, which is very useful for contracting systems. But the equation implies something quite unstable. If there is enough matter in the system, the combined gravity of the matter will compress everything back into a singular state. And to explain all those conditions, Sarkar singularities are needed. Because the hubble expansion rate will act as the constructing rate in the far future. This construction is only for the presence of matter. This does not mean that H<0. This is not possible, because H is always positive. But the presence of matter is somehow generating this construction. Sarkar Singularity indirectly reveals the truth of Raychowdhury equation. Just as we got the Singularity in the past, we will surely get the Singularity in the distant future.

Acknowledgement

None.

Conflict of Interest

None.

References

1. Raychaudhuri, Amalkumar. "Arbitrary concentrations of matter and the Schwarzschild singularity." Phys Rev 89 (1953): 417.

Google Scholar, Crossref, Indexed at

2. Raychaudhuri, Amalkumar. "Condensations in expanding cosmologic models." Phys Rev 86 (1952): 90.

Google Scholar, Crossref, Indexed at

3. Raychaudhuri, Amalkumar. "Relativistic cosmology. I." Phys Rev 98 (1955): 1123.

Google Scholar, Crossref, Indexed at

4. Raychaudhuri, AmalKumar "Relativistic and Newtonian cosmology." Z Astrophys 43 (1957): 161.

Google Scholar