Numerical Investigations of the Influence of Magnetoconvection Radiative Heat and Mass Transfer of Fluid with Nanoparticles on a Nonlinear Stretching Sheet

Nageeb AH Haroun^*, Justin B Munyakazi and Abdulaziz Y A Mukhtar
^*Correspondence: Nageeb AH Haroun, Department of Mathematics and Applied Mathematics, University of the Western Cape, Bellvill, South Africa, Email:

Keywords

Nanofluids • Nonlinear stretching sheet • Conjugate effects • Boundary layer flow

Introduction

The studies of nanofluids have been receiving increased attention worldwide day by day by many thermal scientists and engineers. These researchers have made scientific break through in discovering the unexpected thermal properties of nanofluids which provide opportunities to develop next generation coolants for computers and safe coolants for nuclear reactors. Possible areas for the application of nanofluid technology includes cooling of a new class of super powerful and small computers and other electronic devices for use in military systems and aeroplanes. Also nanofluids could be used in paper and printing, and textiles industries and materials and chemical process industries. It is well known that due to the better performance of heat exchange, the nanofluids can be utilized in several applications such as for chemical production, power generation in a power plant, production of microelectronics, advanced nuclear systems.

In this paper we extend the assumption of a time dependent free stream velocity to the flow of a nanofluid with a zero flux at the boundary. Nanofluids consist of a base fluid containing colloidal suspension of nanoparticles, a term which was first introduced by Choi. Nanoparticles are particles with a range of diameters from 1-100 nanometers. Common base fluids are water, oil and ethylene-glycol mixtures. The literature has revealed that the low thermal conductivity of these common base fluids is a primary limitation in enhancing the performance and the compactness of many devices.

When nanoparticles are added to these base fluids, a drastic increase in thermal conductivity is observed. Narasimhan et al. presented a new theory for forced convection through porous media by fluids with temperature-dependent viscosity. Cheng investigated the effect of temperature-dependent viscosity on the natural convection heat transfer from a horizontal isothermal cylinder of el-liptic cross section. Thermal radiation effect plays a significant role in controlling heat transfer process in polymer processing industry [1]. Thus the effects of thermal radiation on flow and heat transfer process is most desirable in the design of many advanced technological systems which operate at high temperature.

Thermal radiation occurring within the energy convection systems is usually the results of emission by the hot walls and the working fluid. Thermal radiation effects are important when the difference between the surface and ambient temperature is large. In stretching sheet problems thermal radiation is to enhance the thermal diffusivity of the cooling liquid. The Rosseland approximation is used to describe the radiative heat flux in the energy equation. EI-Hakiem and EI-Amin analyzed the influence of thermal radiation and lateral mass flux on non-Darcy natural convection over a vertical flat plate in a fluid saturated porous medium. Pal studied the heat and mass transfer in two-dimensional stagnation-point flow of an incompressible viscous fluid over a stretching vertical sheet in the presence of buoyancy force and thermal radiation. Recently, Pal and Mondal have investigated the combined convection flow of an optically dense viscous incompressible fluid over a vertical surface embedded in a fluid saturated porous medium of variable porosity in the presence of thermal radiation and heat generation/absorption.

This paper aims to study the flow and heat transfer in unsteady mixed convection flow of a nanofluid with buoyancy, thermal radiation, magnetic field and double diffusive effects over a vertical plate which is assumed to be moving in the same direction as the free stream in a porous medium. The plate is maintained at a constant and uniform wall temperature while the nanoparticle fraction on the boundary is passively controlled. The model highly non-linear momentum and heat transfer equations are solved using the SRM method with Gauss-Seidel type of relaxation technique. A detailed description of the method can be found in Motsa. Recently, suggested that bivariate spectral methods are accurate with fast computational times and a high rate of uniform convergence in both space and time. We validate our results by comparison with existing literature for some limiting cases.

Materials and Methods

Mathematical formulation

Steady two-dimensional boundary layer flow of a nanofluid past a stretching surface is considered under the assumptions that the external pressure on the plate in the x-direction is having nanoparticles in the base fluids. The stretching velocity is assumed to be U_w(x)=U₀xm, where U₀ is the uniform velocity, m (m ≥ 0) is a constant parameter and x is the coordinate measured along the stretching surface [2]. The flow takes place above the stretching surface at ≥ y₀. Here y is the coordinate measured normal to the stretching surface. A uniform stress leading to equal and opposite forces is applied along the x-axis so that the sheet is stretched, keeping the origin fixed. It is assumed that at the stretching space after the comma temperature T and the nanoparticle volume fraction C take constant values T_w and C_w whereas the ambient values of temperature T_∞ and the nanoparticle fraction C_∞ are attained as y tends to infinity. The Oberbeck-Boussinesq approximation is employed to the field equations. The governing boundary layer equations that are based on the balance laws of mass, linear momentum, energy and concentration species for the present problem are given as follows:

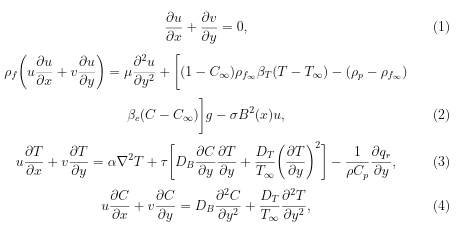
Where u and v are the velocity components in the x and y-direction respectively, g is the acceleration due to gravity, μ is the viscosity, ρ_f is the density of the base fluid, ρp is the density of the nanoparticle, β_T is the coefficient of the volumetric concentration expansion, D_B is the Brownian diffusion coefficient, D_T is the thermophoresis diffusion coefficient, k is the thermal conductivity, (ρc)_p is the heat capacitance of the nanoparticles, (ρc)_f is the heat capacitance of the base fluid, α=k/(ρc)_f is the thermal diffusivity parameter and τ=(ρc)_p/(ρc)_f is the ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid. The associated boundary conditions are:

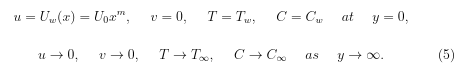
Using the stream function ψ=ψ(x, y), the u and v components of velocity are defined as:

It is assumed that the external pressure on the plate in direction having diluted nanoparticles is constant (yields) [3]. By using the following similarity transformations as introduced by Afify.

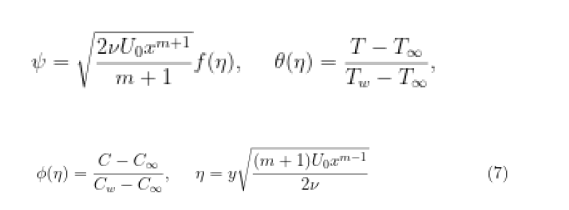
into Eqs. (1), (2), (3) and (4),we get

Here λ is the buoyancy parameter, δ is the solutal buoyancy parameter, Pr is the Prandtl number, Le is the Lewis number, ν is the kinematic viscosity of the fluid, Nb is the Brownian motion parameter, Nt is the thermophoresis parameter, Rex is the local Reynolds number based on the stretching velocity, Gr is the local thermal Grashof number, Gm is the local concentration Grashof number, Nr is the thermal radiation parameter, M is the magnetic parameter and f, θ, φ are the dimensionless stream functions, temperature, rescaled nanoparticle volume fraction, respectively [4].

The corresponding boundary conditions are transformed to:

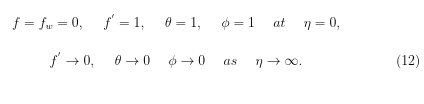
Parameters of engineering interest (Nusselt and Sherwood numbers)

The physical quantities of interest are the skin-friction coefficient, the Nusselt number and Sherwood number which are defined as:

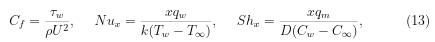
Where the skin friction τ_w, heat transfer from the sheet q_w and mass transfer q_m are given by.

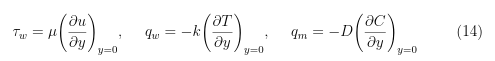
The associated expressions of dimensionless local Nusselt number Nux, local Sherwood number Shx and skin friction coecient Cf are dened as;

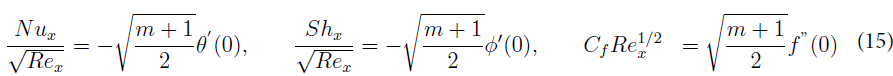
Method of solution

The equations (8) to (10) are highly non-linear, it is difficult to find the closed form solutions. Thus, the solutions of these equations with the boundary conditions (12) were solved numerically using the SRM, (Motsa).

The SRM is an iterative procedure that employs the Gauss-Seidel type of relaxation approach to linearise and decouple the system of differential equations. Further details of the rules of the SRM can be found [5]. The linear terms in each equation is evaluated at the current iteration level (denoted by r+1) and non- linear terms are assumed to be known from the previous iteration level (denoted by r). The linearised form of (8) to (10) is:

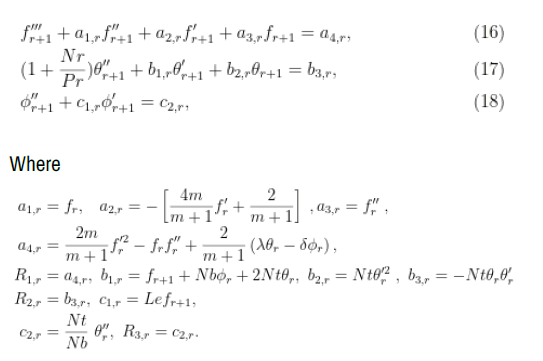
It must be noted that equations (16)-(18) are now linear and, being decoupled, can be solved sequentially to obtain approximate solutions for ff (η), ϑ(η) and φ(η). In this study, the Chebyshev spectral collocation method was used to discretize in. Starting from initial guesses for f, ϑ and φ, equations (16)-(18) were solve iteratively until the approximate solutions converged to within a certain prescribed tolerance level [6]. The accuracy of the results was validated against results from literature for some special cases of the governing equations.

Results and Discussion

Equations (8) to (10) are solved using the SRM. Extensive calculations have been performed to obtain the profiles of quantities such as velocity, temperature and concentration for various values of physical parameters. Numerical investigations to study the various governing parameter effects of heat and mass transfer of nanofluids over a stretching sheet in the presence of magnetic field are reported in this paper. The results are presented graphically and conclusions are drawn to analyze the effects of various physical quantities of interest on velocity, temperature and concentration distribution that have significant effects. Results presented in this paper are in perfect agreement with those published previously. In particular, comparison of present results on ϑ′(0) with those obtained by Anwar et al. In the absence of buoyancy force, magnetic field and thermal radiation show a very good agreement (Table 1) [7].

Table 1. Comperison of reduced nusselt number and reduced Sherwood number for M=0.0, Nr=0.0, f_w=0.0.

Figure 1 depicts the effects of suction parameter on velocity distribution for various values of suction parameter f_w. As expected, the increase in the value of the suction parameter decreases the velocity profiles in the boundary layer. Displays the variation of temperature profiles with suction parameter f_w. It is observed from this figure that as the values of the suction parameter f_w increases the temperature distribution decreases.

Moreover, the thermal boundary layer thickness also decreases with increase in the suction parameter. The influence of suction parameter on concentration profiles is shown in Figure 2 As the values of suction parameter f_w increase, concentration decreases and the concentration boundary layer thickness decreases. Figure 3 represent the velocity and temperature for buoyancy parameter λ. It can be seen that with increase in the values of λ, the velocity increases while temperature decreases [8]. It is interesting to note that there is overshoot in the value of the velocity profiles for higher values of λ>3.0 . It is worth noting that such effect is not observed on temperature profiles.

Figure 4 depict the variation of velocity, temperature and concentration distribution with different values of Lewis number Le. Lewis number defines the ratio of thermal diffusivity to mass diffusivity which is used to characterize the fluid flows where there is simultaneous heat and mass transfer by convection. Effectively, it is also the ratio of Schmidt number and the Prandtl number. It is observed that the temperature and concentration profiles decrease with an increase in the Lewis number whereas reverse effect is observed on the velocity profiles. Figure 5 depicts the velocity profiles for different values of the index parameter. It is observed that the velocity profiles decreases by increasing the index parameter. This is due to the fact that there is decrease in the momentum boundary layer thickness with increase in the value of the index parameter m [9]. The effect of Brownian motion parameter Nb on velocity, temperature and concentration are shown in Figure 6. The boundary layer profiles for the temperature are as in the case of heat transfer in fluids. The velocity and temperature profiles in the boundary layer increase with the increase in the Brownian motion parameter Nb. But the nanoparticle volume fraction profile decreases with increase in the Brownian motion parameter Nb.

It is important to note that the increase in the value of Nr leads to increase in the velocity and temperature profiles as seen from Figure 7 whereas reverse effect of Nr is seen on the nanoparticles concentration profiles. Figure 8 also shows the temperature distribution in presence of thermal radiation to observe that the heat is always transferred from the surface to the ambient fluid [10]. It is noticed from this figure that the temperature in the thermal boundary layer increases with increase in the radiation parameter.

Figure 9 illustrated the typical profiles for temperature ϑ(η) and concentration φ(η) for various values of thermophoretic parameter Nt. It is observed from this figure that an increase in the thermophoretic parameter Nt leads to increase in both fluid temperature and nanoparticle concentration [11]. It is noticed that the temperature and concentration profiles as well as the thickness of the thermal and solutal boundary layer thickness increase with the increase of the values of the thermophoretic parameter Nt. The effect of Prandtl number Pr on the velocity and concentration profiles are depicted graphically in Figure 10. It is observed from this figure that an increase in the values of Prandtl number results in decreasing the velocity profiles whereas reverse effect is seen on the nanoparticle concentration [12].

The effect of Prandtl number Pr on the heat transfer process is shown in the Figure 10. This figure reveals that an increase in Prandtl number Pr results in a decrease in the temperature distribution due to decrease in the thermal boundary layer thickness with an increase in Prandtl number [13]. Physically an increase in the Prandtl number means the slow rate of thermal diffusion which results in decreasing the thermal boundary layer thickness. The effects of Prandtl number on a nanofluid is similar to what has already been observed in the common fluids qualitatively but are different quantitatively. Therefore, this properties are important in nanofluids [14].

Figure 11 depicts the influences of magnetic field on the flow field. It is observed that the presence of transverse magnetic field sets in Lorentz force which results in the retarding the velocity distribution in nanofluids [15]. Thus as the value of magnetic parameter M increases, the retarding force due to increased magnetic field increases and consequently the velocity decreases.

Figure 12 shows the influence of magnetic field parameter M on the thermal field and nanoparticle concentration profiles. It is found that the Lorentz force has the tendency to slow down the motion of the fluid which results in increase its temperature and concentration in the thermal and solutal boundary layer, respectively.

Conclusion

The influence of magnetoconvection radiative heat and mass transfer of fluid with nanoparticles on a nonlinear stretching sheet is analyzed and discussed in details. Governing equations are solved numerically using the SRM method with the Gauss-Seidel type of relaxation technique. The effects of various physical parameters on velocity, temperature and concentration profiles are obtained.

Following conclusions are drawn from the numerical results:

• The velocity of nanofluid decreases for increase in the value of the Prandtl number Pr and index parameter m, whereas reverse trend is found on velocity profiles by increasing the value of λ. The temperature profiles of nanofluids decrease when Pr and λ are increased whereas concentration profile increases for large values of Pr.
• The effect of increase in the value of Brownian motion parameter Nb and thermophoretic parameter Nt is to enhance temperature in the boundary layer region. Also, increasing thermophoretic parameter Nt increases concentration whereas increasing Brownian motion parameter Nb decreases the concentration distribution in the boundary layer
• The effect of thermal radiation parameter Nr is to increase temperature in the thermal boundary layer and velocity profiles in the momentum boundary layer, whereas decreases nanoparticle concentration in the solutal boundary layer.
• The temperature and concentration profiles decrease with an increasing in the Lewis number Le.
• The thickness of velocity boundary layer decreases with an increases in the magnetic field parameter M whereas the thermal and concentration boundary layer thickness increases with increase in the magnetic field parameter M.
• Increase in the suction parameter f_w decreases the velocity, temperature and concentration profiles in the boundary layer.

References

1. Choi, S US and Jeffrey A Eastman. Enhancing Thermal Conductivity of Fluids with Nanoparticles. No. ANL/MSD/CP-84938; CONF-951135-29. Argonne National Lab.(ANL), Argonne, IL (United States), (1995).

   [Google Scholar]

2. Plewes, katherine, Stije J Leopold, Kingston HW and Arjen M Dondorp. "Malaria: What’s New in the Management of Malaria?" Infect Dis Clin 33 (2019): 39-60.

   [Crossref] [Google Scholar] [PubMed]

3. Buongiorno, J. "Convective Transport in Nanofluids." J Heat Transfer 3 (2005): 240-250.

   [Crossref] [Google Scholar]

4. Cheng, Ching-Yang. "The Effect of Temperature-Dependent Viscosity on the Natural Convection Heat Transfer from a Horizontal Isothermal Cylinder of Elliptic Cross Section." Int Commun Heat Mass Transfer  8 (2006): 1021-1028.

   [Crossref] [Google Scholar]

5. El-Hakiem, M A and M F El-Amin. "Thermal Radiation Effect on Non-Darcy Natural Convection with Lateral Mass Transfer." Heat Mass Transfer  2-3 (2001): 161-165.

   [Crossref] [Google Scholar]

6. Pal, Dulal. "Heat and Mass Transfer in stagnation-Point Flow towards a Stretching Surface in the Presence of Buoyancy Force and Thermal Radiation." Meccanica 2 (2009): 145-158.

   [Crossref] [Google Scholar]

7. Pal, Dulal and Hiranmoy Mondal. "Radiation Effects on Combined Convection over a Vertical Flat Plate Embedded in a Porous Medium of Variable Porosity." Meccanica 44 (2009): 133-144.

   [Crossref] [Google Scholar]

8. Ibrahim, F S, A M Elaiw and A A Bakr. "Effect of the Chemical Reaction and Radiation Absorption on the Unsteady MHD Free Convection Flow Past A Semi Infinite Vertical Permeable Moving Plate With Heat Source and Suction." Commun Nonlinear Sci Numer Simul  6 (2008): 1056-1066.

   [Crossref] [Google Scholar]

9. Pal, Dulal. "MHD Flow and Heat Transfer Past A Semi-Infinite Vertical Plate Embedded in a Porous Medium of Variable Permeability." Int J Fluid Mech Res  6 (2008).

   [Google Scholar]

10. Anwar, M I, I Khan, S Sharidan and M Z Salleh. "Conjugate Effects of Heat and Mass Transfer of Nanofluids over a Nonlinear Stretching Sheet." Int J Phys Sci  26 (2012): 4081-4092.

    [Google Scholar]

11. Khan, W A and I Pop. "Boundary-Layer Flow of a Nanofluid Past a Stretching Sheet." Int J Heat Mass Transfer  11-12 (2010): 2477-2483.

    [Crossref] [Google Scholar]

12. Afify, Ahmed A. "Similarity Solution in MHD: Effects of Thermal Diffusion and Diffusion Thermo on Free Convective Heat and Mass Transfer over a Stretching Surface Considering Suction or Injection." Commun Nonlinear Sci Numer Simul  5 (2009): 2202-2214.

    [Crossref] [Google Scholar]

13. Motsa, S S. "A New Spectral Relaxation Method for Similarity Variable Nonlinear Boundary Layer Flow Systems." Chem Eng Commun  2 (2014): 241-256.

    [Google Scholar]

14. Motsa, Sandile Sydney, Phumlani Goodwill Dlamini and Melusi Khumalo. "Spectral Relaxation Method and Spectral Quasilinearization Method for Solving Unsteady Boundary Layer Flow Problems." Adv Math Phys 2014 (2014).

    [Crossref] [Google Scholar]

15. Motsa, Sandile and Zodwa Makukula. "On Spectral Relaxation Method Approach for Steady Von Karman flow of a  Fluid with Joule Heating, Viscous Dissipation and Suction/Injection." Open Phys 3 (2013): 363-374.

    [Crossref] [Google Scholar]