Research Article - (2024) Volume 18, Issue 1
Received: 17-Dec-2023, Manuscript No. glta-23-122959;
Editor assigned: 19-Dec-2023, Pre QC No. P-122959;
Reviewed: 02-Jan-2024, QC No. Q-122959;
Revised: 08-Jan-2024, Manuscript No. R-122959;
Published:
15-Jan-2024
, DOI: 10.37421/1736-4337.2024.18.426
Citation: Oubeid, M. L. Ahmed, A. Benkirane and M. Sidi El Vally. “Nonlinear Parabolic Equations Involving Measure Data in Musielak-Orlicz-Sobolev Spaces.” J Generalized Lie Theory App 18 (2024): 426.
Copyright: © 2024 Oubeid MLA, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
We prove the existence of solutions of nonlinear parabolic problems with measure data in Musielak-Orlicz-Sobolev spaces.
Inhomogeneous Musielak-Orlicz-Sobolev spaces • Parabolic problems • Truncations
46E35, 35K15, 35K20, 35K60
Let Ω a bounded open subset of Rn and let Q be the cylinder Ω × (0, T ) with some given T>0. We consider the following nonlinear parabolic problem:
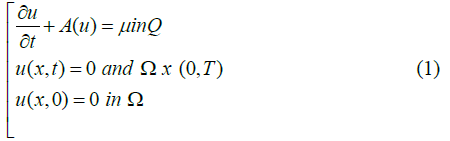
where A=−div (a(x, t, u, ∇u)) is an operator of Leray-Lions defined on D(A) ⊂ W1,xLϕ(Ω), ϕ is an appropriate Musielak-Orlicz function related to the growth of a(x, t, u, ∇u), and μ is a given Radon measure. Solution to problem (1) has been provided firstly by Boccardo-Gallouet, in the setting of classical spaces Lp(0, T; W1,p). Meskine, in prove the existence of solution to problem (1) in the setting of inhomogeneous Orlicz-Sobolev space W01,xLB for any B ∈ PM, where PM is a special class of N-functions and M the N-function. Let us point out that our result can be applied in the particular case when ϕ(x, t)=tp(x), in this case we use the notations Lp(x)(Ω)=Lϕ(Ω) and Wm,p(x) (Ω)=WmLϕ(Ω). These spaces are called Variable exponent Lebesgue and Sobolev spaces. For some classical and recent results on elliptic and parabolic problems in Orlicz-sobolev spaces and a Musielak-Orlicz-Sobolev spaces.
Preliminaries
In this section we list briefly some definitions and facts about Musielak- Orlicz-Sobolev spaces. We also include the definition of inhomogeneous Musielak-Orlicz-Sobolev spaces and some preliminaries Lemmas to be used later.
Musielak-Orlicz-Sobolev spaces
Let Ω be an open subset of Rn.
A Musielak-Orlicz function ϕ is a real-valued function defined in Ω × R+ such that:
a): ϕ(x, t) is an N-function i.e. convex, nondecreasing, continuous, ϕ(x, 0)=0, ϕ(x, t)>0 for all t>0 and
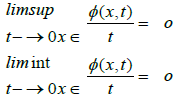
b): ϕ (., t) is a Lebesgue measurable function [1,2].
Now, let ϕx(t)=ϕ(x, t) and let ϕ−1 be the non-negative reciprocal function with respect to t, i.e the function that satisfies
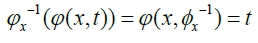
For any two Musielak-Orlicz functions ϕ and γ we introduce the following ordering:
c): if there exists two positives constants c and T such that for almost everywhere x ∈ Ω:
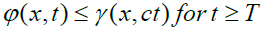
We write ϕ < γ and we say that γ dominates ϕ globally if T=0 and near infinity if T>0.
d): if for every positive constant c and almost everywhere x ∈ Ω we have [3-5].
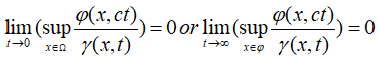
We write ϕ << γ at 0 or near ∞ respectively, and we say that ϕ increases essentially more slowly than γ at 0 or near infinity respectively [6].
In the sequel the measurability of a function u: Ω 1→ R means the Lebesgue measurability. We define the functional
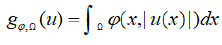
Where u: Ω 1→ R is a measurable function.
The set
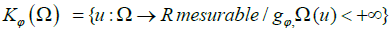
is called the Musielak-Orlicz class (the generalized Orlicz class) [7,8].
The Musielak-Orlicz space (the generalized Orlicz spaces) Lϕ(Ω) is the vector space generated by Kϕ(Ω), that is, Lϕ(Ω) is the smallest linear space containing the set Kϕ(Ω). Equivelently:
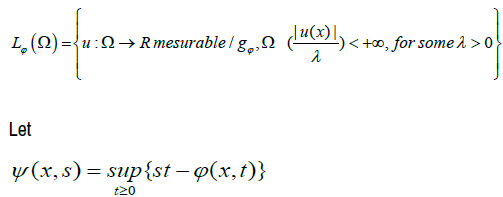
ψ is the Musielak-Orlicz function complementary to (or conjugate of) ϕ(x, t) in the sense of Young with respect to the variable S [9].
On the space Lϕ(Ω) we define the Luxemburg norm:
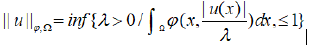
and the so-called Orlicz norm:
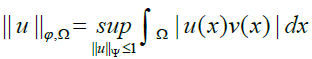
where ψ is the Musielak-Orlicz function complementary to ϕ. These two norms are equivalent [10].
The closure in Lφ(Ω) of the set of bounded measurable functions with compact support in Ω is denoted by Eφ(Ω). It is a separable space and Eφ (Ω) *=Lφ(Ω).
The following conditions are equivalent:
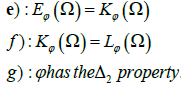
We recall that φ has the Δ2 property if there exists k>0 independent of x ∈ Ω and a nonnegative function h, integrable in Ω such that φ(x, 2t) ≤ kφ(x, t) + h(x) for large values of t, or for all values of t, according to whether Ω has finite measure or not Let us define the modular convergence: we say that a sequence of functions un ∈ Lφ(Ω) is modular convergent to u ∈ Lφ(Ω) if there exists a constant k>0 such that [11].
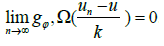
For any fixed nonnegative integer m we define
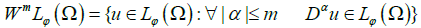
Where α=(α1, α2, ..., αn) with nonnegative integers αi; |α|=|α1| + |α2| + ... +|αn| and Dαu denote the distributional derivatives.
The space WmLφ (Ω) is called the Musielak-Orlicz-Sobolev space [11].
Now, the functional
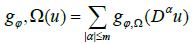
for u ∈ WmLφ(Ω) is a convex modular. And is a norm on WmLφ (Ω).
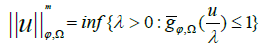
The pair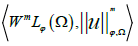 
is a Banach space if ϕ satisfies the following condition:
There exist a constant c>0 such that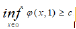 
by Elmahi, A [12].
The space WmLϕ(Ω) will always be identified to a σ(ΠLϕ , ΠEψ) closed
subspace of the product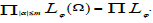 
Let WmoLϕ(Ω) be the σ(ΠLϕ , ΠEψ) closure of D (Ω) in WmLϕ (Ω).
Let WmEφ(Ω) be the space of functions u such that u and its distribution derivatives up to order m lie in Eφ (Ω) and let W0mEϕ(Ω) be the (norm) closure of D(Ω) in WmLφ(Ω).
The following spaces of distributions will also be used:
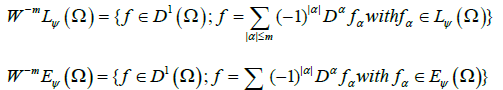
As we did for Lφ(Ω), we say that a sequence of functions un ∈ WmLφ(Ω) is modular convergent to u ∈ WmLφ(Ω)if there exists a constant k>0 such that
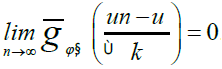
For two complementary Musielak-Orlicz functions φ and ψ the following inequalities hold:
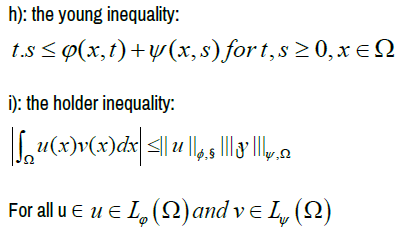
Inhomogeneous Musielak-Orlicz-Sobolev spaces
Let Ω an bounded open subset of Rn and let Q=Ω × 10, T [with some given T>0. Let φ be a Musielak function. For each α ∈ Nn, denote by Dα the distributional derivative on Q of order α with respect to the variable x ∈ Rn. The inhomogeneous Musielak-Orlicz-Sobolev spaces of order 1 are defined as follows [12,13].
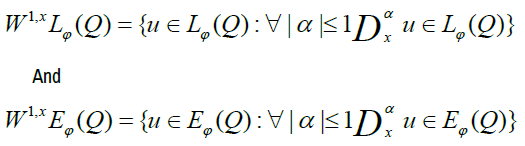
The last space is a subspace of the first one and both are Banach spaces under the norm
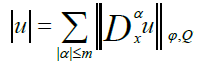
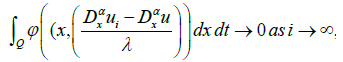
This implies that (ui) converges to u in W1, x Lφ(Q) for the weak topology σ(ΠLM, ΠLψ). Consequently
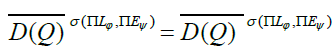
This space will be denoted by Elmahi A and Meskine D [14].
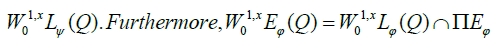
We have the following complementary system
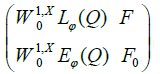
F being the dual space of W1,xEφ(Q). It is also, except for an isomorphism, the quotient of ΠLψ by the polar setW1,xLϕ (Q)⊥ , and will be denoted by F =W−1,xLψ(Q) and it is shown that
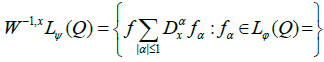
This space will be equipped with the usual quotient norm [14].
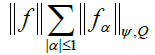
Where the inf is taken on all possible decompositions
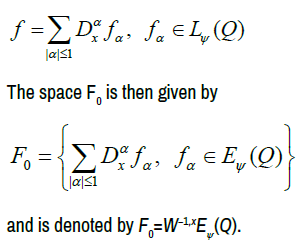
In order to deal with the time derivative, we introduce a time mollification of a function u ∈ Lϕ(Q). Thus we define, for all μ>0 and all (x, t) ∈ Q
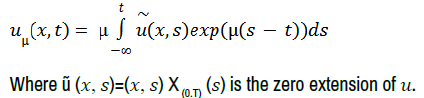
Proposition1:
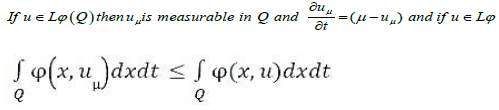
Proof: Since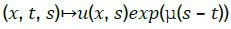 
is measurable in Ω × [0, T]× [0, T], we deduce that u is measurable by Fubini’s theorem. By Jensen’s
integral inequality we have, since
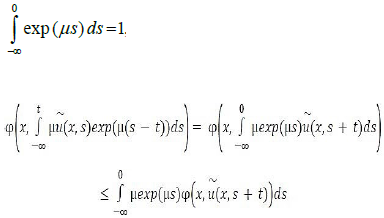
Which implies
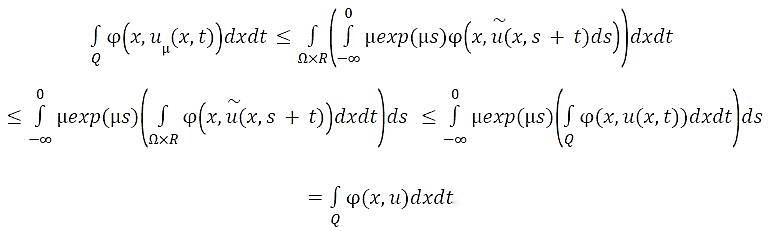
Furthermore
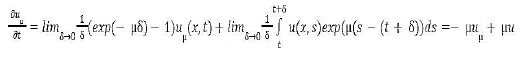
Proposition 2. Assume that (un)n is a bounded sequence in W01,xLφ(Q) Such that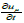 
is bounded in W-1,xLψ(Q)+L1(Q), then un relatively compact L1(Q).
Proof. It is easily by using Corollary 1 of 2.
Let Pφ be a subset of Musielak-Orlicz functions defined by:
Where (x,r)=φ(x, r)/r
We assume that
Pφ≠Φ(2)
Let A: D(A) ⊂W01,xLϕ (Q) →W1,x Lψ (Q)be a mapping givenby
A (u)=−div a(x, t, u,∇u) where a: Q×Rn×Rn be Caratheodory function satisfying for a.e (x,t)∈ Ω and all s ∈ R, ξ, η ∈ Rn with: ξ ≠ η
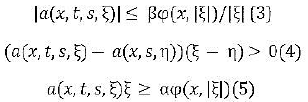
Where α, β>0. Furthermore, assume that there exists D ∈ Pφ such that DoH-1 is a Musielak-Orlicz Function. (6)
Set Tk(s)=(−k, min(k, s)), ∀s ∈ R, for all k ≥ 0
Denote by Mb the set of all bounded Radon measure defined on Q and by T01, ϕ (Q) as the set of measurable functions
Q→ R such that Tk(u)∈W0 1,xLφ(Q)∩D(A) assume that f∈Mb(Ω) and consider the following nonlinear parabolic problem with Dirichlet boundary
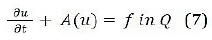
Theorem 1. Assume that (2)-(6) hold and f∈Mb(Q). Then there exists at least one weak solution of the problem
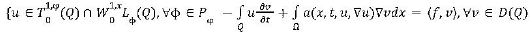
Proof: The proof will be given in two steps.
Step 1: A priori estimates.
Consider now the following approximate equations:
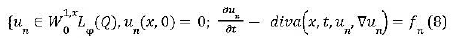
Where fn is a smooth function which converges to f in the distributional
sense and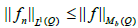 
By Theorem 2 of 3, there exists atleast one
solution of Un of (8), For k>0, by taking Tk(un) as test function in (8), one has
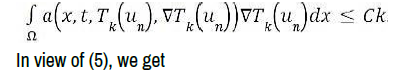
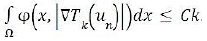
Take a C2 (R), and no decreasing function βk such that for and 2
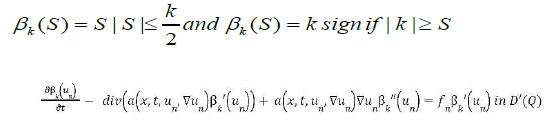
Which implies easily that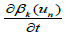 
is bounded in W-1,xLψ (Q) + L1(Q).
Thanks to Proposition 2, we deduce that β(un) is compact in L1(Q).
Then as in (20) and by the proof of Theorem 3 of 1, we deduce that there exists [15].
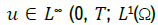such that: un →u almost everywhere in Q and
(almost everywhere in and
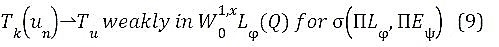
Now, let ϕ ∈ Pφ. By a slight adaptation of the context of Lemma 2.1. of 4, it follows that
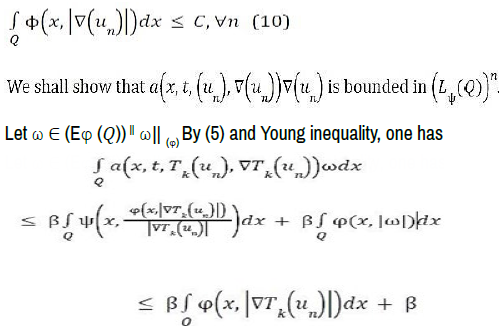
This last inequality is deduced from the fact that ψ(x, φ (x, u)/u) ≤ φ (x, u), for all u>0 and
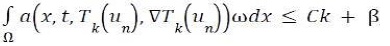
Which implies that (a(x, t, Tk(un), ∇Tk(un))n is a bounded sequence in (Lψ(Q))n.
Step 2. Almost everywhere convergence of the gradient and passage to the limit. Since Tk(u) ∈ W1, x Lφ(Q), then there exists a sequence (αkj) ⊂ D(Q) such that (αkj) → Tk(u) for the modular convergence in W1, x Lφ(Q). For the remaining of this article, χs and χj,s will denoted respectively the characteristic functions of the sets
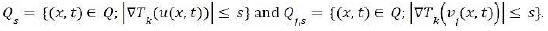
For the sake of simplicity, we will write only ε (n, j, μ, s) to mean all quantities (possibly different) such that
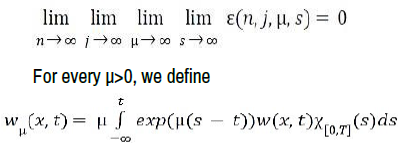
which implies, by using the fact that [17].
The latest integral tends to 0 as n and j go to ∞. Indeed, we have [18].
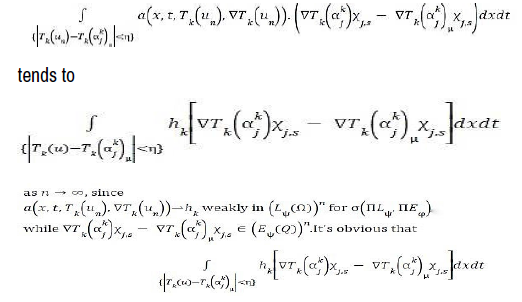
goes to 0 as j, μ → ∞ by using Lebesgue theorem [18,19]. We deduce
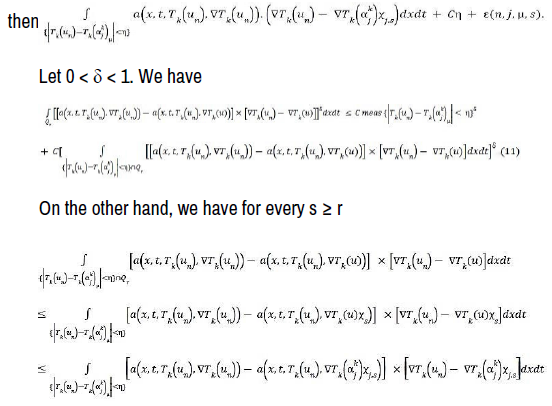
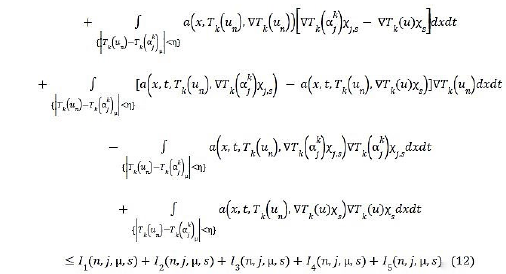
We shall go to limit as n, j, μ and s → ∞ in the last fifth integrals of the last side. Starting with I1, we have [19].
In which we can pass to the limit since we have [20,21].
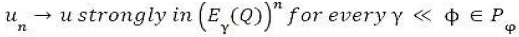
This completes the proof of Theorem 1.
None.
None.
In view of (10), [