Research Article - (2022) Volume 11, Issue 8
Received: 05-Aug-2022, Manuscript No. JACM-22-62252;
Editor assigned: 07-Aug-2022, Pre QC No. P-62252;
Reviewed: 21-Aug-2022, QC No. Q-62252;
Revised: 22-Aug-2022, Manuscript No. R-62252;
Published:
29-Aug-2022
, DOI: 10.37421/2168-9679.2022.11.487
Citation: Mwangi, Gitonga Harun, Joseph Koske and Mathew Kosgei. “Modeling Rainfall Data in Kenya Using Bayesian Vector Autoregressive.”
J Appl Computat Math 11 (2022): 487.
Copyright: © 2022 Mwangi GH, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Time series modeling and forecasting has ultimate importance in various practical domains in the world. Many significant models have been proposed to improve the accuracy of their prediction. Global warming has been a big challenge to the world in affecting the normality of the day to day economic and non-economic activities. It causes far-reaching weather changes, which are characterized by precipitation or temperature fluctuations. Rainfall prediction is one of the most important and challenging tasks in the recent today’s world. In Kenya unstable weather patterns which are associated with global warming have been experienced to a greater extent. The objective of this study was to modeled rainfall patterns in Kenya by use of Bayesian Vector Autoregressive (BVAR). To achieve this objective, the data was first statistically diagnosed using Augmented Dicker Fuller and Granger Causality test. The BVAR model was developed using multiple regression analysis in a system of equations. The model sensitivity was performed using confusion matrix and the F-test was used to compare the variances of the actual and forecasted rainfall values. After the first differencing the data was found to be stationary where Augmented Dicker Fuller (ADF) test was statistically significant with P-values <0.05. The Granger Causality test found that; temperature, atmospheric pressure, wind speed and relative humidity influenced the rainfall time series models in all the regions. The model sensitivity was performed using confusion matrix. The BVAR model developed was statistically significant (R2=0.9896). The sensitivity of the model was 82.22%, making it appropriate for forecasting. In conclusion the Bayesian Vector Autoregressive model developed is suitable and sensitive for forecasting rainfall patterns.
Bayesian vector autoregressive • Vector autoregressive • Forecasting • Global warming
The world is currently generating large datasets in various fields. The amount of data produced and recorded has grown enormously in virtually all fields which include, biomedical, social network, mobile network data, digital archives, electronic trading and weather recording among others. This unanticipated amount of data provides unique opportunities for data-driven decision making and knowledge discovery. However, the massive sample size and high dimensionality of big data introduces unique computational and statistical challenges, which includes scalability and storage capacity, noise accumulation, spurious correlation, incidental endogeneity and measurement errors. In addition, the task of analyzing such large-scale data set comes with momentous challenges and calls for innovative statistical methods designed specifically for faster speed, higher efficiency and accuracy. These challenges are eminent and require new computational and statistical paradigm shift. In spite of the explosion of this big data, specific tools are required for modelling, mining, visualizing, predicting and understanding these large data sets. In many situations, it is easy to predict the outcome given the cause. However, in science more often than not, researchers are faced with the question: when given the outcome of an experiment, what are the causes or the probability of the causes compared to other outcomes? This may best be addressed using Bayesian theory which offers a framework for plausible reasoning and a concept which is more powerful and general tool for handling this problem. To apply Bayesian, data is partition into training and testing sets, where training set is used to develop a model and testing set is for checking the effectiveness of the developed model. This idea of Bayesian theory was championed by Jaynes ET [1]. There had been a growing interest and need in applying big data to many analytical and modelling areas, particularly in time series prediction. The primary model in Multivariate time series analysis is the Vector Autoregressive (VAR). It is the mechanism that is used to link multiple time series variables together. In VAR models, each variable is a linear function of the past values of itself and the past values of all the other variables. It is usually used in simultaneous prediction and structural analysis of a number of temporals observed variables. It is applied when each variable in the system does not only depend on its own lag alone, but also on the lags of other variables. The high- dimensional data set in time series has become common in many areas like in geo-physics, biomedical, econometrics and finance among others. Most of the variables used are correlated and need to be interrelated to give information about a response variable. This crosssectional dependency of variables brings a sharp focus on the problem on how to uniquely understand the interactions among the components of a large dynamic system from the data set. VAR is commonly used for studying high dimensional interrelationships among the components of a multivariate time series, and BVAR was used to treats the VAR parameters as random variables. This study helps to integrate interdependent variables to develop computational efficient model for VAR predictions using Bayesian model. One of the actively researched areas is the weather distribution pattern, about which the understanding is still in its early stages of inferences and robust models are still required.
Kenya has experienced both prolonged droughts or intense flooding every year [2]. Due to the increase in such extreme weat her occurrences, the glaciers around Mount Kenya have disappeared, leading to the drying up of rivers and streams. These weather changes have led to harvest losses and food shortages, as well as landslides, soil degradation and loss of biodiversity among other climatical and economic effects [3]. The diminishing water sources and erratic rainfalls have also reduced the availability of water. Climate variability and changes have adversely affected economic and non-economic sector in which this situation is expected to worsen in the future if drastic measures are not taken. Presently, weather forecast is solved through the help of numerical Atmospheric Circulation Models (ACMs) and other traditional prediction methods, of which it has not solved the erratic weather situation in Kenya. The purpose of this study was to model the rainfall pattern in Kenya using Bayesian Vector Autoregressive and help make appropriate predictions.
The origin of Autoregressive modeling of multivariate stationary processes was in control theory, where canonical tools for identification of linear dynamic systems were Vector-valued Autoregressive Moving Average (VARMA) and state-space representations [4]. According to Lütkepohl H [5], he advocated for the use of higher-order VAR over more general VARMA models due to numerous identification issues of the latter model class. Another person who gave a strong theoretical justification of such a modeling strategy which came from the famous Wald Decomposition Theorem was [6] which ensured that a large class of stationary processes could be represented as potentially infinite order VAR processes. A major function and common application of VAR models is prediction. VAR-based forecasts have proven to be superior to many other methods [7]. In many situations, analyzing a time-series in isolation is reasonable; while in other cases univariate analysis are limited, this was clearly demonstrated by Campbell SD and Diebold FX [8]. One disadvantage of VAR models is that they require time series to have equal lengths in estimation process [11]. This requirement includes a loss of potentially valuable information coming from time series that are longer than others. Bayesian models are different from the classical estimation method. The basic idea of the Bayesian estimation method is to treat the parameters of the model to be estimated as random variables which follow a certain distribution. It is also required to give a prior distribution of the parameters to be estimated based on experiences and combine it with the sample information. Bayes’ theorem is used to calculate the posterior distribution of the parameter to be estimated, thereby obtaining the estimated values with the estimated parameter. Bayesian methods are currently experiencing an increased popularity in the Sciences as a means of probabilistic inference [9]. Among their advantages are the ability to include prior information, the ease of incorporation into a formal decision analytic context, the explicit handling of uncertainty and the straightforward ability to assimilate new information. Bayesian methods are also able to deal with Computational complications arising from the constraints to the positive orthant are avoided through the formulation of a slice sampler on the parameter-extended unconstrained version of the model, [10]. The Bayesian approach has shown to be particularly useful for ecological models with poor parameter identifiability, [11]. The most general time series models have been Box-Jenkins model which assumed that the time series is stationary. There are three stages in developing Box-Jenkin time series model; these are model identification, model estimation and model validation. The problem with Box – Jenkins model is that, for effective fitting of the model it requires at least a moderately long series. The, Yang D, et al. [12] recommended at least fifty observations, while many others recommended at least hundred observations. This problem was sorted by use of Bayesian inferences. The parameters within Bayesian models are stochastic and assigned appropriate probability distributions, [13]. The parameters are treated as random variables and probabilities assigned to these parameters. Bayesian analysis has three components namely; the prior distribution, the likelihood and the posterior distribution. It improves on classical estimations in terms of precision of estimators. The posterior distribution describes the behavior of the parameters after the data is observed and prior assumptions are made. Some recent papers have considered extensions for large BVARs. For example, Koop G and Korobilis D [14] proposed an approximate method for forecasting using large time-varying parameter BVARs. According to Chan JCC and Eisenstat E [15], he estimated Bayesian VARMA containing 12 variables, which he termed to have many variables. A fast process in economic to estimate a large BVAR with a common stochastic volatility was proposed by Carriero A, et al. [16]. These extensions were all found to be outperformed by BVARs with homoscedastic and independent innovations mostly in econometric areas. VARs tend to have a lot of parameters while Bayesian methods that incorporates prior information to provide shrinkage were often found to greatly improve forecast performance [17].
The source of the data was secondary data, which was obtained from Trans- African Hydro-Meteorological Observatory (TAHMO) and Kenya Meteorological stations. To remove scaling, normalization was done through liner scaling technique. It was essential because all the variables used different units of measurements. Also, a variable may have a large impact on the prediction variable only because of its numerical scale or due to its unit of measurement. The technique of linear scaling which is also referred to as min-max normalization estimations, applied a formula that was stated as xval.
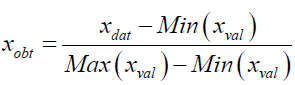
Where; xdat is the value to be normalized, Min(xval) the minimum value, Max(xval) the maximum value, xval the value obtained after normalization. Normalization transformed the data into a common range of between 0 and 1. Thus removing the scaling effects from all the variables. The Vector Autoregressive model (VAR) constitute of a multivariate time series which is applied to examine the dynamic interrelationship between stationary time series variables. VAR model is an extension of univariate to multivariate time series data. It is a multi-system of equations where all the variables are treated as endogenous. Model selection is an integral part of the statistical analysis of VAR models. It is made up of two parts; determination of the lag orders also known as the lag length and the determination of the structures of the VAR coefficient matrices.
The study considered a column vector of k-different variables xt=[x1t,x2t,… ,xkt]' and modeled them in terms of past values of the vector. The result was a Vector Autoregressive of order p or a VAR (p) process which was of the form
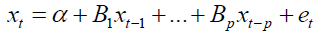
Where, xt is a k × 1 vector stochastic process α is a k × 1 vector of intercept parameters, B1 through Bp are k × k matrices of coefficients, et is a k × 1 vector of white noise process and P is the lag order.
The study considered these two assumptions
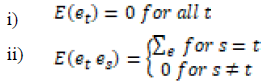
The covariance matrix was also assumed to be a finite positive definite matrix. To develop the coefficient matrix, the lag operators (Δ) method was used. The VAR (p) process was written in lag operator notation, the lag Δ operator was defined in away such that Δxt=x(t-1), that is, it lags (shifts back) the index by one period. Using this lag operator (Δ), the equation
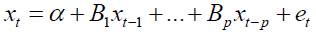
was written as
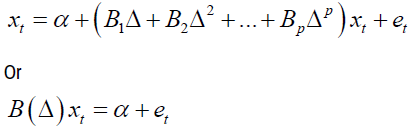
Where
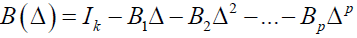
The study considered the model of the form
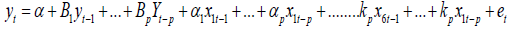
In this study, the following equation formation was considered;
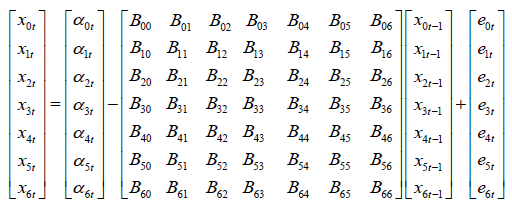
The above form represents the model in matrix form
Where "xit" represented the endogenous variable, which were independent at time period “t” for a specific zone “i”. eit represented the white noise error terms and Bij were the vector matrix of the coefficient. Where i, j = 0,1 …….6. In reduced form, the right-hand side of each equation included lagged values of all dependent variables in the system, no contemporaneous variables.
The Bayesian model considers the VAR as follows, Let xt be an n x 1 random vector that takes values in the domain of real numbers. The evolution of xt the endogenous variable is described by a system of p-th order difference equations in the VAR(p):
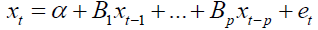
The vector of stochastic innovation, et an independent and identically distributed random variable for each t was the distribution from which et was drawn, which determined the distribution of xt conditional on its past value
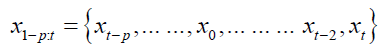
The standard assumption was that errors were Gaussian.
This implies that the conditional distribution of xt was also Normal. Bayesian inference on the xt model amount to updating prior beliefs about the VAR parameters that are seen as stochastic variables, after having observed a sample.
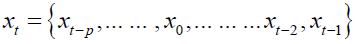
Prior beliefs about the VAR coefficients were summarized by a probability density function and updated using Bayes’ Law.
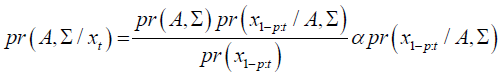
Define as a k x n matrix, with k = n x p +1. The joint posterior distribution of the BVAR(p) coefficients pr(A, Σ) summarized the initial information about the model parameters and the sample information is the likelihood function. The posterior distribution summarizes the entire information available and is used to conduct inference on the BVAR parameters.
Under the assumption of Gaussian errors, the conditional likelihood of the BVAR was
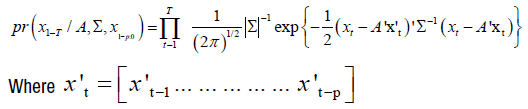
The likelihood in this equation was written in compact form, by using the seemingly unrelated regression representation of the BVAR.
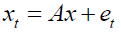
Using this notation and standard properties of the trace operator, the conditional likelihood function was equivalently expressed as
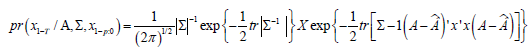
Where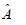 
was the maximum likelihood estimator (MLE)
of A and 
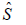the matrix of sums of squared residuals that was
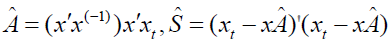
The likelihood was written in terms of the vectorized representation of the VAR
Where xt = vec(xt) and e = vec(e) were Tn x 1 vectors, and ∝ =vec(A) was nk x1. In this vectorized notation the likelihood function was written as
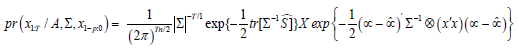
Where consistently, 
was nk x 1. The likelihood function was
used to update the prior information regarding the BVAR parameters.
Having confirmed the Stationarity of the data, as well as the Granger Causality test for all the regions, the model development was readily formulated. This involved lag setting, obtaining the model coefficient and testing their significance.
Lag order selection
When using a BVAR-model it is important to use the correct number of lags. This was done through lag selection criteria of AIC, HQ, SC and FPE.
Lag order selection for zone one: In zone one the lag order was 3 as shown in Table 1.
| AIC(n) | HQ(n) | SC(n) | FPE(n) |
|---|---|---|---|
| 3 | 3 | 3 | 3 |
Model coefficient for zone one
The estimations of BVAR coefficient were analyzed by use of Multiple Least Square method, which gave the following results. Zone one model had the following variables, x.l1, x1.l1, x3.l1, x4.l1, x6.l1, x.l2, x1.l2, x3.l2, x4.l2, x6.l2, x.l3, x1.l3, x3.l3, x4.l3 and x6.l3 with a constant. As indicated in Table 2 the findings showed variable x.l1 had t value of -9.303 and the Pr(>|t|) of 3.07e-06 *** variable x1.l1 had t value of -4.527 and the Pr(>|t|) of 0.001097 **Variable x3.l1 had t value of -4.217 and the Pr(>|t|) of 0.001781 **. Variable x4.l1 had t value of -12.79 and the Pr(>|t|) of 1.59e-07 *** while Variable x6.l2 had t value of -5.368 and the Pr(>|t|) of 4.00e-04 ***. Variable x1.l2 had t value of -2.479 and the Pr(>|t|) of 0.032598 * Variable x1.l2 had t value of -3.777 and the p-value of 0.003621 ** Variable x3.l2 had t value of -4.848 and the Pr(>|t|) of 0.000673 ***. While x4.l2 had t-value 0.462 and the p-value of 0.007417 *** while, x6.l2 had t value of 1.839 and the Pr(>|t|) of 0.012372 *. As indicated in Table 3 the findings showed variable x.l3 had t value of 4.905 and the Pr(>|t|) of 0.001755 ** variable x1.l3 had t value of -4.792 and the Pr(>|t|) of 0.000215 *** Variable x3.l3 had t value of 3.535 and the Pr(>|t|) of 4.31e-06 ***. Variable x4.l3 had t value of 2.263 and the Pr(>|t|) of 0.002771 ** while Variable x6.l3 had t value of 0.036 and the Pr(>|t|) of 0.009524 ** and the constant had at value of 0.264 and the Pr(>|t|) of 0.007147 *** .
The zone one model: x = 0.056 - 0.087x.l1 - 0.142x1.l1 + 0.187x3.l1 - 1.08x4.l1 + 0.072x6.l1 -0.108x.l2 - 0.101x1.l2 +0.37x3.l2 + 0.0165x4.l2 + 0.39x6.l2 +0.44x.l3 +0.14x1.l3 +0.45x3.l3 + 0.39x4.l3 +0.0415x6.l3.
Zone one model coefficient testing: Residual standard error: 4.463 on 20 degrees of freedom. Multiple R-Squared: 0.9896, Adjusted R-squared: 0.9823, F-statistic: 136.1 on 17 and 20 DF, p-value: 4.161e-09
The coefficients were highly significant including the constant. The model had also a great fit, as the adjusted R2 was 0.9823, meaning that 98.23% of a change in the response variable were explained by the regression model.
Lag order selection for zone two: In zone two the lag order was 3 as shown in Tables 2 and 3.
| Variables | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| x.l1 | -0.087072 | 0.00936 | -9.303 | 3.07e-06 *** |
| x1.l1 | -0.142341 | 0.031443 | -4.527 | 0.001097 ** |
| x3.l1 | -0.187338 | 0.044428 | -4.217 | 0.001781 ** |
| x4.l1 | -1.082147 | 0.084548 | -12.79 | 1.59e-07 *** |
| x6.l1 | 0.071938 | 0.008197 | -5.368 | 4.00e-04 *** |
| x.l2 | -0.10808 | 0.040665 | -2.479 | 0.032598 * |
| x1.l2 | -0.101519 | 0.02688 | -3.777 | 0.003621 ** |
| x3.l2 | 0.370303 | 0.076375 | -4.848 | 0.000673 *** |
| x4.l2 | 0.0165 | 0.260521 | 0.462 | 0.007417 *** |
| x6.l2 | 0.392382 | 0.0915 | 1.839 | 0.012372 * |
| x.l3 | 0.43523 | 0.05175 | 4.905 | 0.001755 ** |
| x1.l3 | 0.141775 | 0.08784 | -4.792 | 0.000215 *** |
| x3.l3 | 0.44951 | 0.08137 | 3.535 | 4.31e-06 *** |
| x4.l3 | 0.38672 | 0.07908 | 2.263 | 0.002771 ** |
| x6.l3 | 0.0415 | 0.0165 | 0.036 | 0.009524 ** |
| const | 0.0561 | 0.212506 | 0.264 | 0.007147 *** |
| AIC(n) | HQ(n) | SC(n) | FPE(n) |
|---|---|---|---|
| 3 | 3 | 3 | 3 |
Model coefficient for zone two
Zone two model had the following variables: x.l1, x1.l1, x3.l1, x4.l1, x6.l1, x.l2, x1.l2, x3.l2, x4.l2, x6.l2, x.l3 x1.l3, x3.l3, x4.l3 and x6.l3 with a constant. As indicated in Table 4 the findings showed variable x.l1 had t value of 14.477 and the Pr(>|t|) of 8.13e-10 ***, variable x1.l1 had t value of -16.516 and the Pr(>|t|) of 1.42e-10 ***Variable x3.l1 had t value of 7.120 and the Pr(>|t|) of 5.17e-06 ***. Variable x4.l1 had t value of 10.751 and the Pr(>|t|) of 3.78e- 08 ***while Variable x6.l2 had t value of 3.031and the Pr(>|t|) of 0.008986 **. Variable x1.l2 had t value of 7.290 and the Pr(>|t|) of 3.97e-06 ***, Variable x1.l2 had t value of -7.813 and the p-value of 4.83e-05 *** Variable x3.l2 had t value of 5.773 and the Pr(>|t|) of 4.83e-05 *** while x4.l2 had t-value 6.099 and the p-value of 2.75e-05 *** while, x6.l2 had t value of 1.839 and the Pr(>|t|) of 0.087237. As indicated in Table 4 the findings showed variable x.l3 had t value of 3.905 and the Pr(>|t|) of 0.001585 ** variable x1.l3 had t value of -4.927 and the Pr(>|t|) of 0.000223 *** Variable x3.l3 had t value of 5.530 and the Pr(>|t|) of 7.41e-05 ***. Variable x4.l3 had t value of 3.623 and the Pr(>|t|) of 0.002771 ** while Variable x6.l3 had t value of 0.063 and the Pr(>|t|) of 0.950286 and the constant had at value of 0.291 and the Pr(>|t|) of 0.775018.
| Variables | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| x.l1 | 0.57135 | 0.03947 | 14.477 | 8.13e-10 *** |
| x1.l1 | -2.0109 | 0.12175 | -16.52 | 1.42e-10 *** |
| x3.l1 | 0.72686 | 0.10209 | 7.12 | 5.17e-06 *** |
| x4.l1 | 0.92207 | 0.08577 | 10.751 | 3.78e-08 *** |
| x6.l1 | 0.32639 | 0.10769 | 3.031 | 0.008986 ** |
| x.l2 | 0.85648 | 0.11749 | 7.29 | 3.97e-06 *** |
| x1.l2 | -1.4706 | 0.18822 | -7.813 | 1.80e-06 *** |
| x3.l2 | 0.94533 | 0.16376 | 5.773 | 4.83e-05 *** |
| x4.l2 | 0.95473 | 0.15654 | 6.099 | 2.75e-05 *** |
| x6.l2 | 0.29238 | 0.159 | 1.839 | 0.087237. |
| x.l3 | 0.29352 | 0.07515 | 3.905 | 0.001585 ** |
| x1.l3 | -0.4178 | 0.08478 | -4.927 | 0.000223 *** |
| x3.l3 | 0.44999 | 0.08137 | 5.53 | 7.41e-05 *** |
| x4.l3 | 0.28647 | 0.07908 | 3.623 | 0.002771 ** |
| x6.l3 | 0.00415 | 0.06538 | 0.063 | 0.0095024 ** |
| const | 0.03735 | 0.12818 | 0.291 | 0.0017508 *** |
The zone two model: x = 0.037 + 0.571x.l1 -2.01 x1.l1 +0.727 x3.l1 + 0.922x4.l1 + 0.326 x6.l1 +0.856 x.l2 -1.47 x1.l2 + 0.945 x3.l2 + 0.954 x4.l2 + 0.292 x6.l2 +0.294 x.l3 - 0.418 x1.l3 + 0.449 x3.l3 + 0.286 x4.l3 + 0.00414 x6.l3.
Zone two model coefficient testing: Residual standard error: 0.6973 on 28 degrees of freedom. Multiple R-Squared: 0.9995, Adjusted R-squared: 0.9961, F-statistic: 1919 on 25 and 28 DF, p-value: < 2.2e-16.
The BVAR model was able to confirm that the response variable was affected by both its own lagged values and the lagged values of the predictor variables. These coefficients were all highly significant. The model also had a good fit, as the adjusted R2 was 0.9961, meaning that 99.61% of the change in the response variable was explained by this regression model. It is also worth mentioning that the trend coefficients were highly significant including the constant (intercept) (Table 5).
| AIC(n) | HQ(n) | SC(n) | FPE(n) |
|---|---|---|---|
| 3 | 3 | 3 | 3 |
Lag order selection for Global vector
Global region models had the following variables: x.l1, x1.l1, x3.l1, x4.l1, x6.l1, x.l2, x1.l2, x3.l2, x4.l2, x6.l2, x.l3, x3.l3, x3.l3, x4.l3 and x6.l3 with a constant 9. As indicated in Table 6, the findings showed variable x.l1 had t value of -9.475 and the Pr(>|t|) of 1.26e-06 *** variable x1.l1 had t value of 6.800 and the Pr(>|t|) of 2.95e-05 ***,Variable x3.l1 had t value of -10.894 and the Pr(>|t|) of 3.12e-07 ***, Variable x4.l1 had t value of -8.497 and the Pr(>|t|) of 3.67e-06 ***, Variable x6.l1 had t value of 7.895 and the Pr(>|t|) of 7.41e-06 ***, Variable x.l2 had t value of --5.327 and the Pr(>|t|) of 0.000242 ***, Variable x1.l2 had t value of 2.999 and the Pr(>|t|) of 0.012095 *, Variable x3.l2 had t value of -10.905 and the Pr(>|t|) of 3.09e-07 ***, while x4.l2 had t-value -6.636 and the p-value of 3.68e-05 ***, while Variable x6.l2 had t value of 8.698 and the Pr(>|t|) of 2.92e-06 ***, variable x.l3 had t value of -5.192 and the Pr(>|t|) of 0.000298 ***, variable x1.l3 had t value of 3.991 and the Pr(>|t|) of 0.002117 **, variable x3.l3 had t value of -8.602 and the Pr(>|t|) of 3.26e-06 ***, variable x4.l3 had t value of -3.174 and the Pr(>|t|) of 0.008863 **, variable x6.l3 had t value of 8.248 and the Pr(>|t|) of 4.88e-06 ***, and the constant had a t value of -0.045 and the Pr(>|t|) of 0.000156 ***.
| Variables | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| x.l1 | -1.31387 | 0.13867 | -9.475 | 1.26e-06 *** |
| x1.l1 | 0.69994 | 0.10293 | 6.8 | 2.95e-05 *** |
| x3.l1 | -2.68024 | 0.24603 | -10.894 | 3.12e-07 *** |
| x4.l1 | -4.14922 | 0.04883 | -8.497 | 3.67e-06 *** |
| x6.l1 | 1.88787 | 0.23913 | 7.895 | 7.41e-06 *** |
| x.l2 | -1.07847 | 0.20245 | -5.327 | 0.000242 *** |
| x1.l2 | 0.55664 | 0.18559 | 2.999 | 0.012095 * |
| x3.l2 | -3.11604 | 0.28575 | -10.905 | 3.09e-07 *** |
| x4.l2 | -4.83226 | 0.07282 | -6.636 | 3.68e-05 *** |
| x6.l2 | 3.66172 | 0.0421 | 8.698 | 2.92e-06 *** |
| x.l3 | -0.66616 | 0.12831 | -5.192 | 0.000298 *** |
| x1.l3 | 0.38099 | 0.09545 | 3.991 | 0.002117 ** |
| x3.l3 | -1.17905 | 0.13707 | -8.602 | 3.26e-06 *** |
| x4.l3 | -1.0106 | 0.30184 | -3.174 | 0.008863 ** |
| x6.l3 | 1.92924 | 0.23391 | 8.248 | 4.88e-06 *** |
| const | -0.05123 | 0.14477 | -0.045 | 0.000156 *** |
The global model: x = - 0.05 - 1.31x.l1 + 0.70x1.l1 - 2.68x3.l1 - 4.15x4.l1 + 1.89x6.l1 - 1.08x.l2 + 0.56x1.l2 - 3.12x3.l2 -4. 83x4.l2 + 3.66x6.l2 - 0.67x.l3 + 0.38x1.l3 - 1.18x3.l3 - 1.01x4.l3 + 1.93x6.l3.
Global model coefficient testing: Residual standard error: 5.84 on 21 degrees of freedom. Multiple R-Squared: 0.9496, Adjusted R-squared: 0.969, F-statistic: 1769 on 25 and 21 DF, p-value: < 2.2e-16.
The fitted model explained 96.9% of the model variables which showed that the model fitted the data better. R-squared measures the strength of the relationship between predictor model and the dependent variable on a convenient 0 – 100% scale. It is worth mentioning that the trend coefficient and constant were highly significant. This meant that the model variables were determined by all the variables because there was a significant linear time trend in the data.
The determined lag order was three for the two zones and global vector. The coefficient of the models ranged from 1% and 10% significant levels, where most of them were at the category of 1% and 5%. These depicted the strength of the model coefficients and their predictability ability. The standard error was also determined and it lied between 0.001 to 0.3 which was considered to be small. Having included radiation and wind gust in the model, they did not have any influence and thus they were dropped from the final model. The techniques utilized and the outcomes displayed as a part of this study give experience into the impact of these factors on the meteorological forecasting. This study discovered that weather changes are influenced by several factors that need to be considered and applied to give a good forecast performance. The most important contribution of this study was the forecasting model developed could be used in artificial intelligent areas of meteorological department which would greatly improve their predictability performance.
Climate models only predict a range of possible future scenarios, the extent of how far the future would be should be studied. The outcomes and the technique implemented in this study may contribute as a source of model for forecasting prospective of weather for other countries within the tropical region. The study recommends for further inclusion of more weather variables in the Bayesian vector auto-regression area. Application of other technique like Random Forest and Bootstrapping technique are recommended to check whether the accuracy may be further improved from other models.
None.
Journal of Applied & Computational Mathematics received 1282 citations as per Google Scholar report
