About Filtration in Some Tasks Underground Hydrodynamics

Bereslavsky Edward Naumovich^*
*Correspondence: Bereslavsky Edward Naumovich, Department of Physical and Mathematical Sciences, Saint Petersburg State University, St Petersburg, Russia, Email:

Keywords

Filtration • Infiltration • Evaporation • Groundwater • Free surface • Tongue zhukovsky • Method Polubarinova-kochina • Comprehensive speed • Conformal display • Equations class fuchs

Introduction

The problem on the flow around a tongue was investigated for the first time by Joukowski NE [1], where the modified Kirchhoff method from the theory of jets was used for solving problems with a free surface and a special analytical function, which is widely applied in the theory of filtration, was introduced. After this publication, both the function and the problem, as well as the tongue, were named after Joukowski NE [1]. This study opened the possibility of the mathematical modeling of motions under the Joukowski tongue and initiated investigations of the specified class of filtration flows (see, for example, reviews [2,3]). At the same time, there are no studies devoted to special investigation of the effect of evaporation or infiltration on the pattern of motions. These important physical factors have been disregarded in exact analytical solutions of similar problems until now.

In this work, we studied the effect of evaporation or infiltration by the example of two schemes that arise in the flow around the Joukowski tongue. The first scheme corresponds to the case in which the soil layer is underlain to the entire extent by an impermeable basis and evaporation takes place from the free surface. In the second scheme, the underlying layer represents an entirely well permeable confined water bearing horizon and there is infiltration on the free surface.

We present a uniform technique of solving the problems, which enables us to take into account also other basic filtration characteristics in the investigation (the backwater both from the side of the underlying impermeable basis and the highly permeable confined water bearing horizon and the soil capillarity) and to estimate the joint effect of these factors on the pattern of the phenomenon. Evaporation or infiltration on the free surface are studied using the Polubarinova-Kochina method [2,3] and the ways of conformal mapping [4,5] developed for regions of a special type [6]; in this case, the mixed multiparameter boundary value problems of the theory of analytical functions are solved. Taking into account the typical features of the flows under consideration makes it possible to present the solutions through elementary functions, which makes their use most simple and convenient. The results of numerical calculations are presented and the hydrodynamic analysis of the effect of evaporation or infiltration, as well as all physical parameters of schemes on the filtration characteristics, is given.

Materials and Methods

Flow around the joukowski tongue in the presence of a horizontal confining bed on a foundation (scheme 1)

We consider the 2D (in the vertical plane) steady filtration of a fluid in a homogeneous and isotropic soil layer of thickness T, underlain by a horizontal impermeable foundation (confining bed) under uniform evaporation of intensity ε (0<ε<1) from the free surface (Figure 1).

The flow is provided by the water inflow from the left-hand side of the flooding band AB with the time invariable fluid layer. The impermeable vertical screen in the form of the Joukowski tongue AF of S in length, the basis of which is located inside the layer (Figure 1), serves as the right-hand edge of the flooding band.

We introduce the complex motion potential ω=φ + iψ (φ is the velocity potential and ψ is the stream function) and the complex coordinate

z=x + iy referred correspondingly to κT and T, where κ=const is the soilfiltration coefficient. The problem consists in finding the complex potential ω(z) as the function, which is analytical in the filtration region z and satisfies the following boundary conditions:

AB: y=0, φ= –H; BC: y= –T, ψ=0;

CDE: φ= –y + hc, ψ= –εx + Q; (1)

EA: x=0, ψ=Q, (1)

where hc is the static height of capillary rise of soil waters and Q is the desired filtration flow rate of the water. Assuming that CDE x=L in the second condition in Eq. (1) for the portion CDE, we obtain:

Q=εL. (2)

The problem is solved by using the Polubarinova-Kochina method [2,3], which is based on the analytical theory of the linear differential equations of the Fuks class [7].

We introduce an auxiliary canonical variable ζ and the functions z(ζ), which conformally maps the upper half-plane Im ζ>0 to the flow region z at the correspondence of points ζB=0, ζC=1, ζE=∞ and also the functions dω/ dζ and dz/dζ.

Determining the characteristic parameters of the last functions near the regular special points [2,7],

we find that they are the linear combinations of two branches of the following Riemann function [2]:

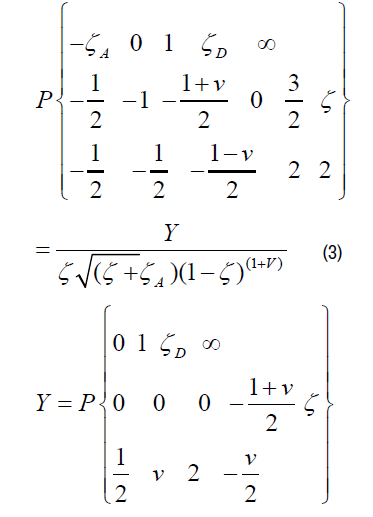
Where 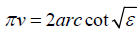It can be seen that point ζ=–ζA is the ordinary point for the function Y representing the last Riemann symbol. The following linear differential equation of the Fuks class with four regular special points corresponds to this symbol:

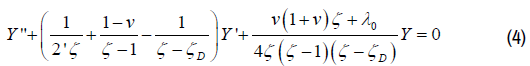
We consider the region of the complex velocity w (Figure 2) corresponding to boundary conditions (1). This region, which is represented by a circular quadrangle with two right angles, the angle of πν at the vertex C and a cut with the vertex at the point D, belongs to the class of polygons in polar grids [4-6]. Similar regions are quite characteristic for many problems of underground hydromechanics: in filtration from a mole sprinkler [8], in the flows of fresh waters in lenses formed above salty waters at rest during filtration from reservoirs and channels [9] and in the flow around the Joukowski tongue in the presence of salty upthrust waters [10] (see also [2,3]).

The replacement of variables ζ=tanh2t transfers the upper halfplane ζ into the horizontal semi-band

Re t>0, 0<Im t<0.5π of the plane t and the integrals Y of Eq. (4), which are constructed by the technique developed previously in [4-6], are transformed to the form

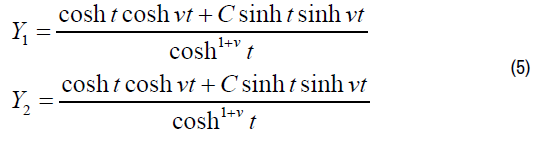
where 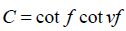a and f (0<a<f<0.5π) are unknown ordinates of the points A and F in the plane t.

Considering relations (3) and (5) and considering that 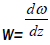, we come to the dependences

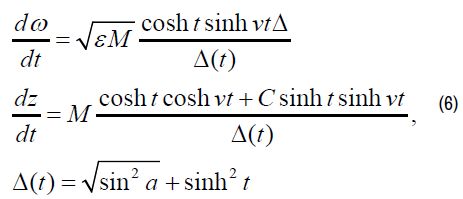
Where М >0 is the scale constant of modeling.

Where λ0 is the accessory parameter. We recall that the prototype ζD of the cut vertex D in Eq. (4) and also the accessory constant λ0 remain unknown in the formulation of the problem.

The writing of representations (6) for different portions of the boundary of the region t with subsequent integration over the entire contour of the auxiliary region of the parametrical variable t results in the expressions for set S, T and H and the desired values of d and L; the flow rate in this case is calculated from formula (2).

In Figure 1, we show the flow pattern calculated at ε=0.6, hc=0.5, T=7, S=3 and H=5. The results of calculations of the effect of determining physical parameters ε, hc, T, S and Н on the sizes of d and L are listed in Table 1. The analysis of the calculations and data in Table 1 allows us to make the following conclusions:

The value of L of the fluid-spread width over the confining bed increases with the static height of the capillary rise of groundwater, the layer thickness and the pressure in the pool and with a decrease in the evaporation intensity and the tongue lengths. For example, it can be seen from (Table 1) that the width L increases three times with increasing parameter ε 4.5 times. If we introduce the dimensionless value of 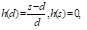, describing the relative height of the groundwater rise behind the tongue for all calculation variants, it proves that d > 0 and, hence,  0 < h < 1, the highest and lowest values of h are achieved precisely with the variation of evaporation intensity: max h(d) = 0.95 at ε= 0.2 and min h(d) = 0.01 at ε= 0.9.

Results and Discussion

Flow around the joukowski tongue in the presence of a highly permeable horizon containing confined underground waters on a foundation (scheme 2)

We consider now another limiting case arising in the problem of flow around the Joukowski tongue, when the soil layer is spread under an easily penetrable confined water-bearing horizon ВС, the pressure in which has a constant value of Н0 and there is a uniform infiltration of intensity ε (0 ≤ ε<1) on the free surface (Figure 3). Then far from the tongue (at х → ∞), the depression curve is horizontal and located at the height H0 above the water-bearing horizon. In this scheme, boundary conditions (1) on the portions АВ and ЕА are retained and the conditions on the boundaries ВС and CDE are replaced with the following:

BC: y= –T, φ= –H0; (7)

CDE: φ= –y - T, ψ=εx + Q.

The region of complex velocity w corresponding to boundary conditions (1), (7), which represents a circular triangle with two right angles and with a cut with the vertex at the point D, is shown in Figure 4. Similar polygons are quite typical in the drainage problems [11-13] under the motion of groundwater through dams with diaphragms [14,15], etc., for example, [2,3].

Usually such regions are transferred into rectilinear polygons with the help of inversion with the subsequent use of the Christoffel–Schwarz formula, which, as a rule, results in the solution through elliptical functions and integrals.

Contrary to these possibilities, we propose below a way based on the direct use of an equation of the Fuks type, the integrals of which are the trigonometric functions sine and cosine.

For this purpose, it is convenient this time to choose a different correspondence of points in the upper halfplane ζ:

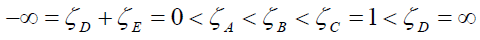
Applying the Polubarinova-Kochina method, we find that, in this case, the functions and are the linear combinations of two branches of the following Riemann function [2,7]:

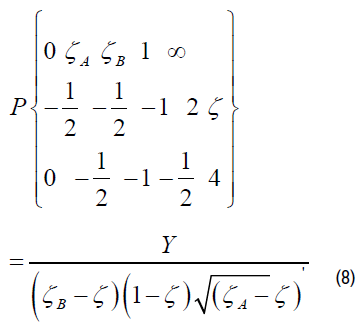
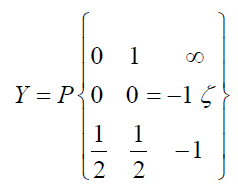
From consideration of the region of w and relation (8), it follows that the points ζ=ζA and ζ=ζВ are the ordinary points for the function Y representing the last Riemann symbol. The linear differential equation of the Fuks class with three regular special points corresponds to it:

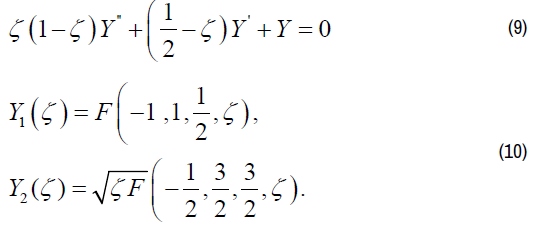
The replacement of variables ζ=sin2t changes the upper half-plane ζ into the vertical semiband 0<Re t<0.5π, Im t>0 of the plane t at the correspondence of vertices tE=0, tC=0.5π, tD=∞ and integrals (10) are transformed to

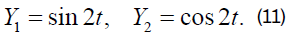
Considering relations (8) and (11), we come to the desired dependences

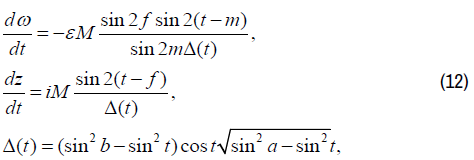
where m and f are the prototypes of the points М and F (0<m<f<a<b<0.5π) related as

Unknown constants a, b, m and М are determined from the set of equations consisting of the expressions for S, Т, Н, H0 and with fixation of the abscissa хC of the point С of the depression curve.

We note the limiting case of the flow related to the absence of infiltration, i.e., at ε=0. With considering the parameters m, f and ε from Eq. (13), the solution of the problem in the case when ε=0 follows from dependences (12) at m=0, i.e., when the points С and Е of the depression curve in the plane w merge at the origin of coordinates with the point М of zero velocity. Thus, we obtained the solution of the problem considered for the first time by Vedernikov VV [13] but only with another method and in a different form, i.e., through conventional trigonometric functions (Table 2).

Equation (9) is the Gaussian equation [7]. Its canonical integrals in the vicinity of the point ζ=0 are expressed through the hypergeometrical function F (α, β, γ, ζ) [7] and have the following form in this case.

Conclusion

In Figure 3, we show the flow pattern calculated at ε=0.6, T=7, S=3, Н=7, H0=3 and xC=100. The results of calculations of the effect of the determining physical parameters ε, S, Н and H0 on the value of d and the parameter h(d) are listed in Table 2 (the negative values of d mean that the free surface rises behind the tongue above the abscissas abscissa axis). The analysis of calculations and data in (Table 2) enable us to make the following conclusions. An increase in the intensity of infiltration and pressure in the pool and in the underlying horizon, as well as a decrease in the layer thickness and the tongue length, result in decreasing value of d. We recall that, previously in Scheme 1, a decrease in the evaporation intensity, on the contrary, resulted in similar behavior of the value of d. From Table 2, it can be seen that it is exactly the infiltration on the free surface that induces the greatest effect on the depth d, it being quite substantial that the value of d varies almost 84 times with increasing the parameter ε 4.5 times. Contrary to Scheme 1, where only positive values of d were observed, here it proved that d<0 for the overwhelming majority of the calculation variants, i.e., the depression curve rises above the abscissa axis and, hence, h(d)>1. In this case, the values of the parameter h can be quite significant: From Table 2, it follows that h(d)=4.91 for S=1. It can be seen that, as in scheme 1, the lowest value of h is achieved now upon variation of the infiltration intensity ε on the free surface: minh (d)=0.98 at ε=0.2.

References

1. N. E. Joukowski, Infiltration of Water through Dams. Collected Works (Gostekhizdat, Moscow, 1950), Vol. 7, [in Russian].
2. Polubarinova-Kochina, P. Ya. "Theory of the motion of ground water." Nauka, Moscow (1977).

Google Scholar

3. Entov, V., S. Numerov, P. Polubarinova-Kochina and I. Charnyi. "Development of Investigations on the Theory of Filtration in the USSR (1917–1967)." (1969).

Google Scholar

4. Bereslavskii, E. N. and P. Ya Kochina. "Some equations of the Fuchs class in hydro-and aeromechanics." Fluid Dyn 27 (1992): 603-607.

Google Scholar, Crossref , Indexed at

5. Bereslavskii, KN and P. Ya Kochina. "Differential equations of the Fuchs class encountered in some problems of mechanics of liquids and gases." Fluid Dyn 32 (1997): 619-625.

Google Scholar

6. Kochina, P. Ya, E. N. Bereslavskii and N. N. Kochina. "Analytical Theory of Linear Differential Equations of the Fuks Class and Certain Problems of Underground Hydromechanics." Preprint 567 (1996).

Google Scholar 

7. Golubev, V. V. "Lectures on the analytic theory of differential equations." Gostekhizdat, Moscow (1950).

Google Scholar

8. Bereslavskii, E. N. "Spin fresh water salt water during filtration of the cold snap sprinkler." Appl Math Mech 53 (1989): 350-355.

Google Scholar

9. Bereslavskii, E. N. "The intake of purified fresh water with filtration from a reservoir." Appl Math Mech 54 (1990): 714-718.

Google Scholar, Crossref  

10. Bereslavskii, E. N. "A hydrodynamic model for the forcing back of stagnant salt water by fresh filtration water flowing around a Joukowski tongue." Dokl Phys 43 (1998): 775-778.

Google Scholar 

11. V. V. Vedernikov. K teorii drenazha // Report of the Academy of Sciences of the USSR, 1939, v. XXIII, i. 4, p. 335 – 337
12. V. V. Vedernikov. K teorii drenazha // Report of the Academy of Sciences of the USSR, 1948, v. LIX, i. 6, p. 1069-1072.
13. Vedernikov, V. V. "Filtracija pri nalichii drenirujushego ili vodonosnogo sloja." Report of the Academy of Sciences of the USSR 69 (1949): 619-622.

Google Scholar

14. Nelson-Skornyakov, F. B. "Pritekanie gruntovyh vod so svobodnoj poverhnost’ju k sisteme dren pri glubokom zaleganii vodoupora." Izv AS USSR, OTN (1941): 126-128.

Google Scholar

15. Nelson-Skornyakov, F. B. "Dvizhenie gruntovoj vody so svobodnoj poverhnust’ju cherez plotinu s dvumja diafragmami." Izv AS USSR (1941): 39-44.

Google Scholar