Research Article - (2022) Volume 7, Issue 5
Received: 04-May-2022, Manuscript No. PE-22-49452;
Editor assigned: 06-May-2022, Pre QC No. P-49452;
Reviewed: 18-May-2022, QC No. Q-49452;
Revised: 23-May-2022, Manuscript No. R-49452;
Published:
30-May-2022
, DOI: 10.37421/2472-1042.2022.7.154
Citation: Connock, Martin, Mubarak Patel, Daniel Gallacher and Aileen Clarke. “When do Rayleigh and Weibull parametric models predict the same results?” Pharmacoeconomics 7 (2022): 154.
Copyright: © 2022 Connock M, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Background: Most Health Technology Appraisals (HTA) model survival data using a conventional set of six parametric distributions. Alternative and potentially useful distributions exist and could also be exploited. Rayleigh 2 parameter (R2P) and Weibull models are both defined with two parameters and exhibit monotonic hazard; the Rayleigh model is relatively unused in HTA and should not be regarded as just a special case of the Weibull model.
Aim: To explore circumstances where the predictions from R2P and Weibull models may differ or coincide.
Method: Stata software was used to model sample survival data with R2P and Weibull models and to compare the predicted hazard and survival from each parametric.
Results: R2P models generate different predictions to Weibull models except in the special case where the Weibull shape parameter equals or closely approaches two and the Weibull hazard prediction is linearly increasing. When compared to Weibull models R2P models may generate a better fit to observed data according to conventionally used indicators of goodness of fit.
Conclusion: Rayleigh modelling of survival warrants inclusion in the survival modelling undertaken in Health Technology Appraisals.
Health technology • R2P
The particular method selected for modelling overall and progression-free survival is often important in HTAs. In most appraisals it appears conventional for investigators to employ six “standard” parametric distributions (exponential, Weibull, Gompertz, lognormal, loglogistic, and generalised gamma) to explore survival modelling. Taken together these can generate a wide variety of survival and hazard predictions (Figure 1).
Figure 1. Illustration of the variety of survival and hazard predictions from parametric distributions commonly used in HTA. W = Weibull, LL = loglogistic, LN = lognormal, G = Gompertz.
Other parametric distributions and methods have been developed [1- 3], but are not necessarily wired into readily available software (e.g. Stata, and flexsurv platform in R [4]). Rayleigh 2 parameter (R2P) models predict a linear hazard that increases through time with slope that depends on the data modelled; predicted survival and hazard are described by [1]:
S(t) = (exp (-λ0 t + λ1 t2) )
h(t) = λ0 + 2 λ1 t
where λ0 > 0 and λ1 ≥ 0
Alternative parameterizations termed Rayleigh can be found in the literature that have a single parameter (R1P) and generate linear hazard with slope depending on the magnitude of the parameter. These and other similar parameterizations are shown in Table 1, where they can be seen to be equivalent to each other for certain values of λ. The advantage of the 2 parameter Rayleigh model over the traditional 1 parameter version is that it does not have to assume 0 hazard rate at time 0.
| Name | Hazard Function | Survival Function |
|---|---|---|
| Linear Polynomial | λ0 + λ1 t + λ2 t2 |  |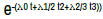
| Exponential | λ0 |  |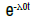
| Rayleigh 1 parameter | 2λ1 t |  |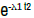
| Rayleigh 2 parameter | λ0 + 2λ1 t |  |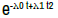
| Weibull |  |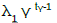
 |
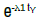Using several published data sets we aimed to ascertain in what circumstances the predictions of R2P and Weibull models coincide or differ.
It is evident that a linearly increasing hazard will yield a survival curve that would exhibit a trajectory that gradually increases in downward slope through time before in flexing when fewer patients remain at risk. To illustrate differences and similarities between R2P and Weibull models we therefore selected several real data sets with this general trajectory: one with a very smooth survival curve [5] another with several changes in survival trajectory but generally conforming to that expected from a linearly increasing hazard [6] and for purposes of contrast and comparison we selected a third data set in which the survival descending trajectory is fairly linear [7]. The data sets were obtained using the method of Guyot P, et al. [8], from published KM survival plots. Weibull and R2P models were fit in Stata using the streg command (Weibull) and the stgenreg package of Crowther MJ, et al. [9]. Results are presented in Figures and text.
In the first data set (microfracture) the KM plot is smooth with a trajectory of gradually increasing downward slope. The Weibull model for this data has a shape parameter almost equal to 2 (2.032349). Weibull and R2P parameters and AIC/BIC values are shown in Table 2. Figure 2 graphs the survival and hazard predicted by each model. In this special case where the Weibull scale parameter is extremely close to 2 the predictions from the two models are nearly identical as also are the AIC BIC values for the models. The alternative parameterisations e.g. “h(t) = 2 θ time” provide the same output as the two parameter Rayleigh because λ0 is vanishingly small.
| Data source | Weibull | Rayleigh | Rayleigh | Weibull |
|---|---|---|---|---|
| scale shape | λ0 λ1 | AIC BIC | AIC BIC | |
| Microfracture | 0.0040098 | 3.85e-09 | 252.4714 | 252.4505 |
| 2.032349 | 0.0043426 | 258.267 | 258.2462 | |
| Olaparib | 0.0069264 | 0.0093257 | 266.4826 | 270.4121 |
| 1.530169 | 0.0013019 | 272.6578 | 276.5873 | |
| Atezolizumab | 0.0457028 | 0.0531509 | 370.1087 | 369.7873 |
| 1.06053 | 8.02e-10 | 376.048 | 375.727 |
Figure 2. Kaplan-Meier plots and parametric predictions from Rayleigh and Weibull modelling KM = Kaplan-Meier, R = Rayleigh 2 parameter, W = Weibull, EXP =exponential.
In the second data set (olaparib) the KM trajectory again has a gradually increasingly downward slope. The Weibull shape parameter (1.53) lays between 1 and 2. The R2P model generates different hazard and survival predictions than the Weibull model (Figure 2) and generates lower AIC / BIC values suggesting a superior fit. On AIC / BIC values the Rayleigh single parameter model generates a poorer fit than the R2P model (Figure 3).
Figure 3. Kaplan-Meier plots and parametric predictions from Rayleigh two and one parameter modelling.
In the third data set (atezolizumab) the KM trajectory is almost linearly descending and the Weibull shape parameter (1.06) is very close to unity and the predicted survival almost the same as an exponential model fit to the data. The R2P λ1 parameter is vanishingly small so that R2P hazard virtually becomes h(t) = λ0 as for an exponential model. R2P, Weibull and exponential model predictions of survival are almost identical as are the hazard predictions of R2P and exponential models. The alternative single parameter parametrisation of the Rayleigh e.g. “h(t) = 2 θ time” provides very different output (linearly increasing hazard) with very poor survival fit to the observed data (Figure 3).
Hazard function λ1 γ tγ-1 weibull 2 parameters
A Weibull model has a single scale parameter (λ) that multiplies with time raised to the power of the shape parameter (γ) that may take a variety of values resulting in monotonically increasing or decreasing hazard trajectories (Figure 1). In the special case of shape parameter =1 the hazard is constant through time and predictions are the same as those of an exponential model. When shape is <1 the hazard decreases monotonically and when > 1 increases monotonically. In the special case of shape =2 the resulting Weibull hazard increases linearly as does the hazard for Rayleigh models and predictions from Rayleigh and Weibull models will be the same (as for example in the microfracture dataset). This represents a relatively unusual special case that rarely crops up, in most situations the Weibull shape will not be 2 and the Rayleigh and Weibull models will deliver different predictions (as is the case for the olaparib dataset), and one or the other may deliver a superior fit relative to the alternative.
Hazard function λ0 + 2λ1 t Rayleigh 2 parameters
A Rayleigh survival model [1], has two parameters, one multiplies with time raised to the power two while the other multiplies with time raised to power of one. This generates a linear hazard that increases through time with steepness depending on how large a value is given to λ1. When λ1 is very small the hazard becomes nearly flat through time (like an exponential model) and predictions become indistinguishable from exponential modelling; if the Weibull model for the data set happens to take a shape parameter of 2 the Rayleigh and Weibull predictions will coincide. The Rayleigh R2P model is unlikely to fit well to data that has a general trend of decreasing hazard though time as λ1 will tend to take a value <0, so that if a Weibull model delivers a shape parameter <1 it is possible that a Rayleigh model will not converge and may be inappropriate.
Beyond AIC and BIC, other considerations may apply regarding the suitability of parametric models for extrapolation beyond observed data. In the NICE STA process, clinical experts are often consulted to provide estimates of survival beyond the timelines used in the clinical trials. For example, clinical experts may provide expected five- and ten-year survival estimates for a new technology where the clinical trial only extends to a few years. A well-fitting parametric model may not necessarily generate what clinical advisors consider plausible; it is also possible that estimates from different clinicians can vary considerably. Visual inspection of the parametric curves overplayed on the Kaplan-Meier plots and the observed log-cumulative hazard versus modelled log-cumulative hazard plots will illustrate the extent of differences between models and observed data. A further test, the Hosmer-Lemeshow plot test [10], may be conducted and looks at the correspondence between observed logcumulative hazard and modelled log-cumulative hazards. A range of different tests can be carried out to inform decisions.
Rayleigh models offer an independent modelling of survival that can be useful in some circumstances and may deliver superior fit to data than that seen with Weibull or other conventional models often employed in HTA. Rayleigh two-parameter models are not just special cases of Weibull modelling; rather, a special case Weibull model with shape = 2 will be equivalent to a Rayleigh model when λ0 = 0. In most circumstances the two parameter Rayleigh model predictions differ from alternative models. Exceptions are Weibull models that fortuitously have a shape parameter close to =2 or =1.
Funding
Not applicable
Conflicts of interest/Competing interests
None
Availability of data
Not applicable
All authors contributed to the concept of the paper and contributed to construction of the text
Ethics approval
Not applicable
We are grateful to Professor Karl Peace for the helpful dialogue surrounding the Rayleigh distribution.
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Pharmacoeconomics: Open Access received 106 citations as per Google Scholar report
