The Effect of Variable Properties on Magnetohydronamics (MHD) Flow through a Vertical Channel

Areo AO^1*, Olajide OA¹, Adegbite P¹, Anifowose BU¹ and Adetunde I^2
*Correspondence: Areo AO, Department of Pure and Applied Mathematics, Ladokve Akintola University of Technology, Ogbomoso, Oyo State, Nigeria, Email:

Keywords

Variable viscosity • Heat generation • Porosity • Thermal conductivity • Magnetic field

Introduction

Analytical solution of MHD stagnation-point flow and heat transfer of casson fluid over a stretching sheet with partial slip studied by Nandy SK [1], showed that for a casson fluid, the magnitude of velocity is bigger than viscous fluid, and that increasing the velocity slip parameter lead a drop in flow velocity, and the same qualitative result applies for the thermal slip parameter on temperature. He formulated the governing equations and use similarity transformation to convert them to a set of ordinary differential equations which he then solves analytically using homotopy analysis method.

Several investigations have concerned themselves with the theory of MHD. Prakash D, et al. [2] investigated the effect of heat generation on MHD free convective flow of viscous fluid in a vertical channel in the presence of variable properties. Thermal conductivity and viscous fluid vary linearly with temperature. The non-dimensional governing equations are evaluated using different transform method (DTM), the effects of physical parameters involved are evaluated through. The solutions are compared with the numerical one by one by Runge-Kutta Felberg along with shooting technique. The result of Bhattacharyya k [3] on MHD Stagnation-point flow of Casson fluid and heat transfer over a stretching sheet with thermal radiation, shows that, the thickness of the velocity boundary layer decreases as the velocity ratio parameter and magnetic parameter are increased, also the velocity boundary layer thickness for Casson fluid is greater than that of Newtonian fluid.

Jha BK, et al. [4] used numerical study to investigate the transient freeconvective flow of reactive viscous fluid in a vertical channel formed by two infinite vertical parallel plates. A theoretical analysis is also presented to find the expression for temperature, velocity, skin-friction and Nusselt number for the stead fully developed flow using perturbation technique.

The effect of variable viscosity and thermal conductivity on MHD free convective heat and mass transfer flow past an inclined surface with heat generation studied by Hazarika GC and Gogoi L [5] where both the fluid velocity and thermal conductivity are assumed to vary as inverse linear function of temperature, using similarity transformations, the governing partial differential equation s are reduced to ordinary differential equations which are solved numerically for boundary condition by applying shooting method Sivaraj R, et al. [6] analyzed the problem of steady, mixed convective, laminar flow of two incompressible, electrical conduction and heat absorbing immiscible fluids in a vertical porous channel filled with viscoelastic fluid in one region and viscous fluid in other region. A uniform magnetic field is applied in transvers direction, the fluids rise in the channel driven by thermal buoyancy force associated with thermal radiation. An exact solution is obtained for the velocity, temperature, skin friction and Nusselt number distribution. The study of Manjunatha G, et al. [7] on the impact of variable transport properties and slip effects on MHD Jeffrey liquid fluid flow, shows that an increase in the magnetic parameter reduces the velocity as well as temperature.

Analysis of unsteady magnetohydrodynamics radiative thin liquid film flow, heat and mass transfer over a stretching sheet with variable viscosity and thermal conductivity was carried out by Pal D and Saha P [8]. Computed results for unsteadiness, temperature ratio, radiation parameter in the presence/ absence of the viscous and ohmic heating are analyzed and discussed. Computed result results show that the viscous and ohmic dissipations reduce the temperature gradient profiles in the thin liquid film. Thermal radiation decreases the cooling rate of the thin liquid film, but the reverse effect is seen by increasing the Prandtl number. Salawu SO and Dada MS [9] investigate the radiative heat transfer of variable viscosity and thermal conductivity effects on inclined magnetic field with dissipation in a nondarcy medium, where governing partial differential equations are transformed into a system of ordinary differential equations using the similarity variable transformations and solved numerically using shooting technique together with fourth- order Runge-Kutta method. The worked on the effect of relative magnetic field, chemical reaction, heat generation and Newtonian heating on convection flow of Casson fluid over a moving vertical plate embedded in a porous medium by Khan D, et al. [10]. The result showed that time (t) has a similar effect on velocity, temperature, and concentration profile, while porous medium, heat generation parameter, Prandtl number, Schmidt number, and chemical reaction have a decreasing effect.

Akindele M, et al. [11]. observe the effect of nonlinear radiative heat and mass transfer on MHD flow over a stretching surface with variable conductivity and viscosity. The nonlinear equation governing the flow are reduced to ordinary differential equation by appropriate similarity variable and quantity, the nonlinear equations are computationally solved by applying shooting techniques coupled with Nachtsheim- Swigert method for asymptotic satisfaction of boundary conditions by fourth order Runge Kutta technique. Effect of variable fluid properties on magnetohydrodynamic flow of nanofluid past a flat plate studied by Srinivasa CT, et al. [12] their results shows that the fluid velocity and temperature increase for the variable viscosity and thermal conductivity parameter. Areo AO, et al. [13] studied MHD effects on porosity and concentration in an unsteady flow in a vertical channel. The nonlinear governing equations of motion with concentration equation incorporate variable porosity were employed and solved analytically using a perturbation technique. The effects of the flow were determined through the physical parameters from the course of the investigation, it was revealed that fluid temperature increase within the channel with increase porosity.

Mathematical Formulation

The system under consideration is a laminar non-isothermal flow of an incompressible fluid between two vertical parallel plate positioned at y′ = 0 and y′ = h with uniform temperature T₁ (hot wall) and T₂ (cold wall) The flow is assumed in the x=direction which is taken vertically upward along the vertical plates and the y-axis is taken normal to the plates as shown in figure 1. Since the plates are infinite in lengths, the velocity, temperature and concentration fields are function of y′ only. All fluid properties are considered constant except the influence of variable viscosity, thermal conductivity and density variation with temperature. In addition, the influence of density and expansion coefficient variation in terms in the momentum and energy equations are negligible. The steady natural convection fully developed flow in a vertical channel under the usual Bussines q approximation is governed by the following equations [14-16].

The flow governing equations now can be written as

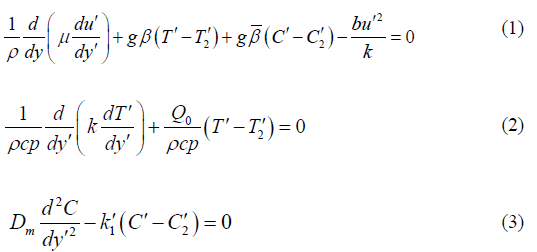
whereC′ is the concentration, T′ is the temperature, (β ,β ) are the temperature and concentration coefficients of volumetric expansion, ν is the kinematic viscosity, the velocities are (u′,v′) along the axes ( x′, y′) . The equations (1) - (3) must be solved subject to the boundary conditions: At

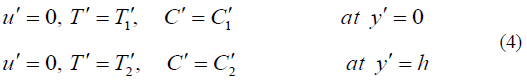
Now we introduce the following non-dimensional variables

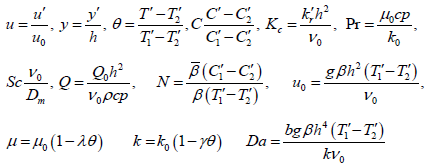
When Pr is the Prandit number, N is buoyancy parameter, Sc is the Schmidt number, k_c is the chemical reaction parameter and Q is the heat source parameter.

Follow (Umavathi and Shecar), the fluid velocity (μ ) is assumed to be varying linearly as a function of temperature in the form:

(6)

In general, (a∠0) for gases and (a > 0) for liquids, where a is the dimension of k⁻¹ and eqn. (6) can be rewritten in the form:

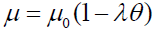(7)

Where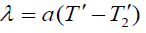

Similarly, following (Anjzli and Pralcask) the fluid conductivity (K) is assumed to vary linearly as a function of temperature in the form:

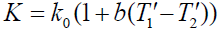(8)

In general, (b⟩0) for fluids such as water and gases while (b∠0) for fluids such as lubricating oils where b is the dimension of λ ⁻¹ and eqn.(8) can be rewritten in the form:

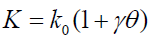(9)

Where 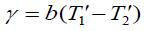. In addition, the range of variables of γ Schilchting and Gerster k for air 0 ≤γ ≤ 5 for water 0 ≤γ ≤ 0.12 and for lubrication oil 0 0 −0.1≤γ ≤ 0 μ and K are constants when the temperature is T₁ . The reference temperature is taken to be T₂

Using equations (4), (7), (9), and equations (1) - (4) reduce to:

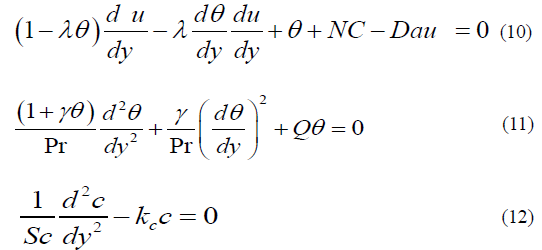
The boundary conditions with the new variables are

Equations (10) - (12) with boundary conditions (13) describe the heat and mass transfer along a vertical plate in the presence of a magnetic field under variable viscosity and thermal conductivity. The governing equations (10) -(12) with boundary conditions given in (13) are solved numerically by using the 4^th order Runge-Kutta shooting method with the of maple 18 software.

Results and Discussion

This paper shows the combined effects of temperature, dependant viscosity, variable porosity and thermal conductivity on natural convection flow in a vertical channel. The nonlinear coupled governing differential equations have been solved numerically using Runge – Kutta method of order four with the aid of Maple 18 software to obtain results for temperature, velocity and concentration fields. After considering a laminar non-isothermal flow of an incompressible fluid between two vertical parallel plates, the following discussion was ensued; (Figures 1 and 2) show the effect of heat generation parameter Q on temperature and velocity profiles. This figure shows that increasing value of Q, increases the temperature profile which is physically true since increasing the heat source parameter amplifies the applied temperature causing the fluid temperature to increase and also, it strengthens the convection current within the channel leading to an increase in fluid velocity. (Figure 3) shows the effect of variable viscosity parameter temperature profile. It was observed that increasing that variable viscosity decreases fluid temperature while fluid velocity increases within the channel. This is expected since increasing (λ ) leads to an increase in the fluid viscosity. Increasing fluid viscosity poses a hindrance to thermal diffusivity thereby causing heat accumulation leading to increase in fluid temperature.

(Figure 4) shows the effect of variable viscosity parameter on velocity profile. It was observed that increasing that variable viscosity increases fluid temperature while fluid velocity decreases within the channel. This is expected since increasing (K) leads to an increase in the fluid viscosity. (Figure 5) shows the effect of variable viscosity parameter on velocity profile. This figure shows that increasing value of Sc. decreases the velocity while increasing the chemical reaction parameter decreases both fluid velocity and temperature. The physical meaning of the observed trend is that growing N increases buoyancy due to mass transfer and hence, an increase in fluid velocity. (Figure 6) shows the effect of variable viscosity parameter on temperature profile. It is observed from these figures that increasing viscosity increases fluid temperature. This is expected since increasing (v) leads to an increase in the fluid viscosity. Increasing fluid viscosity poses a hindrance to thermal diffusivity thereby causing heat accumulation leading to increase in fluid temperature. An increase in chemical reaction parameter decreases both fluid velocity and temperature. This was observed in (Figure 7). Also, increasing chemical reaction causes a decrease in fluid concentration and this weaken convention due to mass transfer which consequently decrease fluid velocity. The influence of Buoyancy parameter is illustrated in (Figure 8). It was observed from the figure that an increase in Buoyancy increase fluid velocity. In (Figure 9) the effect of Darcy number (Da) was studied on velocity profile. The study reveals that the velocity profile decreases s slightly with increase of Da.

Conclusion

In this study, the influence of temperature dependant viscosity, thermal conductivity and variable porosity on natural convention flow through a channel was considered. The governing differential equations for temperature, velocity and concentration fields were solved using Runge-Kutta of order four with the aid of Maple 18. The results from the exact and numerical methods were observed with excellent agreement the results of fluid flow within the channel reveals the following:

• Increase value of variable viscosity and darcy number parameter favor the growth of velocity profile

• Higher value of variable viscosity parameter and heat generation parameter increases the temperature profile.

References

1. Nandy, Samir Kumar. "Analytical solution of MHD stagnation-point flow and heat transfer of casson fluid over a stretching sheet with partial slip."  Int sch res notices (2013).

Google Scholar, Crossref, Indexed at

2. Prakash, D., N. Elango and I. Sadham Hussain. "Effect of heat generation on MHD free convective flow of viscous fluid in a vertical channel in the presence of variable properties." In AIP Conf Proc 2277 (2020) : 030016

Google Scholar, Crossref, Indexed at

3. Bhattacharyya, Krishnendu. "MHD stagnation-point flow of Casson fluid and heat transfer over a stretching sheet with thermal radiation." J Thermodyn 2013 (2013).

Google Scholar, Crossref, Indexed at

4. Jha, Basant K., Ahmad K. Samaila, and Abiodun O. Ajibade. "Transient free-convective flow of reactive viscous fluid in a vertical channel." Int Commun Heat Mass Transf 38 (2011): 633-637.    

Google Scholar, Crossref, Indexed at

5. Hazarika, G. C and Lurinjyoti Gogoi. "Effects of variable viscosity and thermal conductivity on mhd free convective heat and mass transfer flow past an inclined surface with heat generation.”  Int J Comput Appl 167 (2017).

Google Scholar, Crossref, Indexed at

6. Sivaraj, R., B. Rushi Kumar and J. Prakash. "MHD mixed convective flow of viscoelastic and viscous fluids in a vertical porous channel." Appl  Math: An International Journal (AAM) 7 (2012): 6.

Google Scholar, Crossref

7. Manjunatha, G., C. Rajashekhar, Hanumesh Vaidya and K. V. Prasad, et al. "Impact of variable transport properties and slip effects on MHD jeffrey fluid flow through channel."  Arab J Sci Eng 45 (2020): 417-428.

Google Scholar, Crossref, Indexed at

8. Pal, Dulal and Prasenjit Saha. "Analysis of unsteady magnetohydrodynamic radiative thin liquid film flow, heat and mass transfer over a stretching sheet with variable viscosity and thermal conductivity." Int J Comput Methods Eng 22 (2021): 400-409.

Google Scholar, Crossref

9. Salawu, S. O and M. S. Dada. "Radiative heat transfer of variable viscosity and thermal conductivity effects on inclined magnetic field with dissipation in a non-Darcy medium." J Niger Soc Math Biol 35 (2016): 93-106.

Google Scholar, Crossref, Indexed at

10. Khan, Dolat, Arshad Khan, Ilyas Khan and  Farhad Ali, etal. "Effects of relative magnetic field, chemical reaction, heat generation and Newtonian heating on convection flow of casson fluid over a moving vertical plate embedded in a porous medium."  Sci Rep 9 (2019): 1-18.

        Google Scholar, Crossref, Indexed at

11. Akindele M., Okedoye, Akindele M., Kelvin O. Ogboru and John Damisa, et al. "Two-Dimensional dissipative non-slip mhd flow of arrhenius chemical reaction with variable properties."

Google Scholar, Crossref

12. Srinivasa, C. T., J. K. Singh, B. J. Gireesha and M. Archana. "Effect of variable Fluid Properties on Magnetohydrodynamic flow of nanofluid past a flat Plate."  J Nanofluids 8 (2019): 520-525.

Google Scholar, Crossref, Indexed at

13. Areo A.O., Akinpelu F. O and Adetunde I. A. “Mhd effects on porosity and concentration in an unsteady flow in a vertical channel.” Int j mech eng appl 10: (2021)  30-50

Crossref

14. Ajibade A. O and Ojeagbase P. O. Effect of variable viscosity and thermal conductivity on free convection heat and mass transfer flow through a vertical channel, Comput Math 8 (2019): 1 – 7.

Google Scholar, Crossref

15. Hassanien, I. A., A. H. Essawy and N. M. Moursy. "Variable viscosity and thermal conductivity effects on heat transfer by natural convection from a cone and a wedge in porous media." Arch Mech 55 (2003): 345-356.

Google Scholar, Crossref, Indexed at

16. Munir, M. S and R. S. R. Gorla. "Combined convection from a vertical flat plate with temperature dependent viscosity and thermal conductivity." Int J Fluid Mech Res 29 (2002).

Google Scholar, Crossref, Indexed at