Evaluation of Risk Modelling in Emerging Equity Markets through the Lens of Extreme Value Theory

Zarmina Ali Khan^1* and Arshad Hassan^2
*Correspondence: Zarmina Ali Khan, Department of Finance, Capital University of Science & Technology, Islamabad, Pakistan, Email:

Keywords

Value-at-risk (VaR) • Extreme value theory (EVT) • Backtesting • Risk forecasting • Emerging markets • Corporate finance system

Introduction

The financial risk modeling is an integral part of risk management. Value at risk is the most commonly used measure for estimation of market risk. It quantifies the maximum loss of an asset that may occur over a given period at a specific confidence level [1]. The main concern in estimating the value at risk is the appropriate assumption about the distribution of returns, that generally exhibit well-known stylized characteristics such as; fat tails, non-normality, asymmetric conditional volatility and volatility clustering [2]. Manganelli and Engle [3] state that the main difference among VaR models is in reliably unfolding of the distribution of returns. Therefore, the main challenge is selecting an appropriate distribution of returns to capture the time-varying conditional volatility of future return.

The VaR models are conventionally used under the various distributional assumptions like gaussian distribution and other distributions include Student-t distribution and GARCH processes. During the last two decades, financial markets have seen many downfalls in the form of the global financial crisis, the Russian financial crisis, Chinese market crash. The expanding instability in the global financial markets makes it necessary to assess the risk associated with extreme events.

An extensive treatment in finance underscores the importance of rare events in risk management which may result in extreme movement in prices or unexpected boom or bust in stock markets. Therefore, in order to model market risk, it is desireable to address the issue of heavy tails of distributions. In response, VaR measures based on the Extreme Value Theory (EVT) have been developed, which allows us to module the tails of distributions and to estimate the probabilities of the extreme movements that can be expected in financial markets. The idea behind extreme value theory is that tail distribution should independently be examined to assess the extreme loss.

Most of the literature on the measurement of EVT based VaR is primarily focused on developed markets of Europe and the United States. Research on the estimation of quantile extremes in emerging equity markets is still limited. Especially, the literature on the comparison of VaR models and their preductive performance on the basis of fitness for use across different emerging markets is rare. It is generally believed that emerging market exhibit higher risk. The general perception to exhibit higher risk in emerging markets appears to be correct as these markets are exposed to additional risks arising from fragile financial system, exchange rate fluctuations, macroeconomic and political uncertainties cross border capital flows and less mature capital markets.

The extant literature provides substantial evidence of use of GARCH family models to estimate the VaR in stock markets and currency markets under different distributional assumption like Gaussian distribution, Student-t distribution and generalized errors distribution [4-9]. However, generalized errors distribution (GED) is considered weak in capturing the asymmetry in financial returns and thus resulting in biased estimates of VaR [10]. Giot and Laurent [11] and Diamandis, et al. [12] add the asymmetric distributional assumption in the returns of developed and emerging equity markets and conclude that VaR models based on asymmetric distributions have a better predictive performance in comparison to VaR models based on symmetric distributions. Similarly, the tail behavior of equity returns has been discussed in individual markets and regions [13].

The increasing financial uncertainties have challenged the financial market participants to develop and improve the existing methodologies used in measuring risk these recent extreme market conditions raise a question on existing risk management models. This criticism on models provides an opportunity to explore the phenomenon through different theoretical framework especially through the lens of models that can deal with the rare events that create disasters [14]. Extreme value theory (EVT) provides a set of robust tools for modeling the behavior of extreme and catastrophic outcomes that fall in the tails of empirical distributions. Numerous studies exhibit the potential of EVT to estimate the extreme quantiles of the distribution of returns in the stock and currency exchange markets using the maximum blocks based on generalized extreme values (GEV) distributions [15-22]. The peaks over thresholds (POT) represents another alternative that allows the treatment of extreme risk in the tails of distribution; this approach’s cornerstone is the generalized Pareto distribution (GPD). Studies based on the assumption of GPD conclude that VaR models based on the unconditional EVT outperform conventional parametric models in the estimation of VaR, particularly in the extreme quantiles [23,24]. In contrast, Kittiakarasakun and Tse [25] provide empirical evidence that VaR-GARCH models achieve greater predictive performance than the EVT-Static VaR models in the stock markets of Asia. These studies argue that main drawback of the unconditional EVT stems from its incapability of capturing the impact of unexpected changes in market conditions on the estimation of VaR, besides the assumption that returns are identically and independently distributed (i.i.d.), which is not valid in modern financial markets. To overcome this problem, McNeil and Frey [26] propose the use of conditional EVT to estimate VaR in two stages. The first stage consists of the adjustment of a GARCH model to estimate the conditional volatility and filter the series of returns to obtain a standardized series of i.i.d. residuals. In the second stage, conditional EVT is applied to the distribution of standardized residuals to capture the heteroscedasticity in extreme returns arising from stochastic volatility.

Mogel and Auer [33] compare EVT based approaches for univariate VaR prediction in stock, commodity, bond and currency markets and provide guidance for choosing the appropriate estimation strategy in practice. The study recommends that the Box-Cox method is the most promising unconditional approach followed by historical simulation. For conditional setting, the historical simulation took the lead before the peak over threshold method indicating that return filtering had a stronger positive effect on historical simulation than on the EVT-based approaches. The objective of this study is to bridge the above gap through examining the tail behavior of the returns in emerging markets using extreme value theory. Specifically, the first objective of this study is to explore the applicability of EVT in emerging market and the second is to compare the performance of EVT based models to identify the methods that are appropriate to assess emerging market risks. Furthermore, it accounts for the time-varying volatility, asymmetric effects and heavy tails in return distribution and combines GARCH based model with EVT which is likely to generate more accurate quantile estimates for forecasting VaR. Finally, the out-of-sample predictive performance of the competing models is assessed through dynamic backtesting using the Kupiec’s point of failure test and Christofferson’s independence test.

Methodology

The extreme value theory employs two main approaches; Block Maxima Model (BMM) based on generalized extreme value distribution (GEV) and peak over threshold model (POTM) based on generalized Pareto distribution (GPD).

This block maxima model selects the maximum value from the sample of normally distributed return. The term M is the maximum value from the sample size T. Fisher-Tippett-Gnedenko theorem states that, like constants are as well as some non-degenerate distribution function H is in the following form:

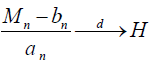
Here, the value of H may relate to any of these distributions:

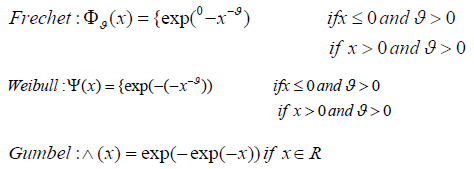
According to the theorem, M may follow any of the following distribution of Frechet, a Weibull or a Gumbel. If the value for ξ =0, it means the distribution is Gumbel. Whereas, if ξ <0, the shape is from Weibull distribution. Similarly, if ξ>0 means positive, the distribution is Frechet. The distribution is given below:

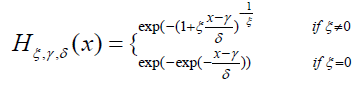
For 1+ ξ (x-γ)/δ > 0, the location and scale parameters are represented by γ and δ, which represents the limiting distribution of the extreme maxima.

The following results can be obtained by inverting the equation with any respective confidence level α i.e:

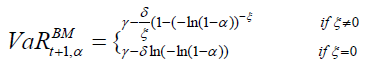
The second method of extreme events is based on exceedances over the threshold, called a peak over a threshold that is fitted to the exceeded distribution from GPD. This method has an advantage over BMM, as it uses available data more efficiently. The generalized Pareto distribution uses the function of exceedances as:

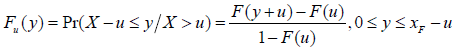
Then generalized Pareto distribution is as under:

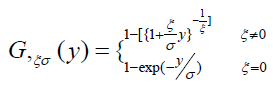
Here, ξ is the shape parameter and σ is the scale parameter. If ξ >0, the distribution is heavy-tailed distribution, if ξ = 0, the distribution is lighttailed and if ξ <0 the distribution is a short-tailed Pareto type II distributions. Generally, all financial data streams are heavy-tailed [18]. Therefore, VaR under generalized Pareto distributions can be estimated as under:

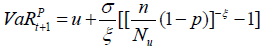
Finally, backtesting is the generalized method used to test the accuracy of the model. The back-testing technique compares the expectation of losses with the actual loss. Violation ratio is used to compare the expected number of violations with actual VaR. It is the conventional method of backtesting the accuracy of forecasting models. The ideal value for violations ratio is 1, which states that the number of expected violations is equal to the number of observed violations. But in financial data, it is not always possible to get exactly 1. Danielson [28] suggest that violation ratio between 0.8-1.2 may be used as a rule of thumb for the efficacy of the model.

Another technique of backtesting, the Kupiec POF test, is introduced in 1995 to investigate the degree of failure. This test uses the binomial distribution approach. The test estimates the exceptions by comparing it with the likelihood ratio. The LR suggests that whether the probability of exception matched with the probability P, at defined confidence level. The model said to be accepted or may provide true forecasting of risk if the LR is less than χ² value of 1 degree of freedom.

The POF test statistic is

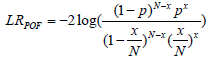
Where N is the number of observations and x is the number of times a model failed. It is assumed that, if the chi-square value does not exceed a critical value, the null hypothesis is accepted which states that model did true forecasting of risk. Similarly, the Christoffersen’s interval test is introduced in 1998 to test the clustering effect. It tests the dependence of events between connected days. The independence test is:

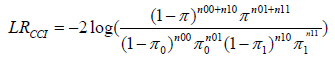
In the above equation, the n00, n01, n10, n11 represent the sequence of failure and /or no failure. The null hypothesis assumes no clustering, means the probability of violation of tomorrow does not depend on today’s violation.

The sample of the study consists of daily closing indices of twelve emerging markets for the period of 1/2000 to 12/2018. The emerging market includes Brazil (Bo Vespa), Russia (MOEX), India (Nifty 50), Bahrain (Share BAX), China (Shanghai), Colombia (COLCAP), Malaysia (FTSE), Thailand (SET INDEX), Argentina (Marvel), Bangladesh (Dhaka Stock Exchange), Pakistan (KSE 100) and Sri Lanka (CSE). The returns are calculated by taking the first difference of natural log of prices for each series,

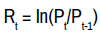
where Rt represents the returns earned in the day ” t,” P_t is the closing price of index at the time “t”, whereas P_t-1 is the closing price of index at time “t-1”

Result and Discussion

The statistical behavior of data is examined through descriptive statistics and results are reported in Table 1. The mean shows the average return earned by a market in aday. The maximum average return is earned by Pakistan (0.0007) followed by Sri Lanka and Russia with average return of (0.0006). Bourses of Pakistan, Russia, Sri Lanka, Brazil and India outperforms the exception of the Bangladeshi market which is riskiest market followed by Argentina and Russia. Low-risk markets include Bahrain, Malaysia and Thailand the returns are negatively skewed for all markets except for Bangladesh and Sri Lanka. The kurtosis exhibits leptokurtic behavior which is an indicator of fat tails distribution and non-normality of data. The maximum and minimum return also signals the presence of extreme events in relevant markets. The relationship of risk and return is inefficient in these markets, as the more risky stock is not able to gain highest returns (Table 1).

The focus of extreme value theory is to analyze the extreme outcomes. The block maxima approach under the assumption of generalized extreme value distribution and unconditional and conditional peak over threshold approach under the assumption of generalized Pareto distribution are applied to explore tail behavior. The VaR estimates for the long position are reported at 95% and 99% of confidence level.

Table 2 represents the BMM estimation of VaR, the comparison of expected with observed violations and selection of model with back testing techniques of violation ratio, Kupiec ratio and Christoffersen’s test.

The VaR estimates are higher for Argentina, Russia and Sri Lanka as 9% a day as compared with other emerging markets. Whereas, Bahrain and Malaysia exhibits minimum loss of 2% in a day, with 95% of confidence interval. The similar expectation of lass is noticed with 99% of confidence interval except for Bangladesh, as it reports 25% of higher risk reported in a day.

In the next phase, the original or observed number of violations in VaR estimates are reported and compared with the expected number of violations. The comparison shows that BMM expects more loss than actually happens in a market, but the reliability of these violations are checked in next column with violation ratios. The estimated violation ratio for all emerging markets are not in prescribed range of which is 0.8-1.2 [28]. Similarly, the modern back testing techniques like Kupiec and Christoffersen’s reliability test also prove the failure of BMM for VaR estimates, as none of the emerging markets likelihood ratio comes in range.

Peak over threshold Table 3 provides that Russia, Argentina, Brazil and China reported highest VaR estimates of 4%- 3% respectively in a day. The other emerging markets like Bahrain, Bangladesh, Columbia, Malaysia, Sri Lanka and Thailand reported 1% of expectation of loss in a day with 95% of confidence interval. The reported expectation of loss is different for 99% of confidence interval as Russia tends to be more risky market as 7% expectation of loss. Whereas, the minimum expectation of risk is more or less same as 95% of confidence interval.

The next columns reports the expected violation of peak over threshold model with actual violations reported in emerging markets. The gap between the two violations are very minimum, which may favour the peak over threshold model. The completed analysis of model with 95% of confidence interval, the reported violation ratio are in provided range of 0.8 to 1.2 for Argentina, Bahrain, Brazil, Pakistan and Sri Lanka. The Kupiec Test also supports, the GPD static model as the likelihood ratio is less than 3.67 in all emerging markets except for Bangladesh and Columbia. To check the clustering effect, in most of the emerging markets, null hypothesis of no clustering is accepted.

The models results are more or less same with 99% confidence interval, the reported observed violations are less than the observed ones, but they are near to them. According to violation ratio and Kupiec test, this model estimate ideal VaR for Argentina, Brazil, Columbia, Pakistan and Sri Lanka. All emerging markets show the clustering effect except for the market of Columbia.

Finally, the two-step method reported in Table 4 is used to estimate VaR through residual of GARCH process. The VaR estimates are too small for almost all emerging markets at 95% and 99% confidence level. The maximum loss per day is reported by Argentina (0.2%), whereas the markets of Bahrain, India, Malaysia, Pakistan, Russia, Sri Lanka and Thailand reported 0.0% expectation of loss, meaning that these markets are free from risk, or does not possess any risk.

To check model reliability, the expected and observed violations are compared; the reported results show more difference between both of violations, which essence that GPD dynamic underestimate risk in all emerging markets. None of the violation ratio comes in prescribed range, which clearly questioned the authenticity of model. The results of Kupiec and Christoffersen’s test also conforms to results of violation ratio. Hence, the two step residual GARCH model may not provide the true forecasting of risk in these emerging markets.

A comparison of these models for estimation of VaR indicates that unconditional POT model is better for risk forecasting in fat-tails in emerging market like Argentina, Brazil, Columbia, Pakistan and Sri Lanka, as the observed violations are equal to the expected ones in approximately 42% markets. The block maxima model and conditional POT model are complete failures.

It is further noticed that with the increase confidence level, the dependence and reliability of model decreases.

Conclusion

With the latest updates to Amazon's SEO algorithm, you can use external traffic to influence your product rankings. One such method is to utilize Google SEO. To do this, companies need to create a blog and add direct links to your product listings in your posts, writing informative yet engaging articles in a way that excites your audience. This will increase sales and thus improve product rankings.

If views are low compared to total sales, this can affect your ranking on Amazon. This can be controlled by introducing a login page. If you're a Brand Registered seller, you can create custom landing pages for the products you want to highlight.

Acknowledgments

Value-at-risk has always attracted the attention of academician and analysts and adopted widely after the financial crisis of the 1990s. It is generally estimated under various distributional assumptions while considering leptokurtic behavior, asymmetries, non-normal behavior of data and volatility clustering, etc but tails are ignored. However, a study of the behavior of the tails is more exciting as it is generally less observable but has a high impact. This study provides an insight into the predictive performance of symmetric and asymmetric EVT-based models in emerging markets for a period of 2000 to 2018.

The predictive performance of unconditional POT model based on generalized Pareto distribution is found better in comparison to block maxima model based on GEV distribution and conditional POT model based on GPD. Block maxima model overestimates returns and thus underestimates risk. On the other hand, condition POT model underestimates returns and thus overestimates risk. However, the problem of clustering in volatility is there. The VaR model is neither country nor market-specific, the model for risk estimation is global is nature as unconditional POT model based on generalized Pareto distribution can be applied to most of emerging markets, to forecast risk.

These results have important policy implications for portfolio managers as well as regulators. Portfolio managers may get additional insight in making decisions regarding resource allocation, portfolio diversification and risk management. The regulators may step to reconsider the disclosure requirement, governance laws and efforts to promote the role of equity markets in respective countries.

References

1. Kupiec, Paul H. “Techniques for verifying the accuracy of risk measurement models.” J Deriv 95 (1995).

Google Scholar, Crossref

2. Christoffersen, Peter F. "Evaluating interval forecasts." Int Econ Rev (1998): 841-862.

Google Scholar, Crossref

3. Engle, Robert F. and Simone Manganelli. "CAViaR: Conditional autoregressive value at risk by regression quantiles." J Bus Econ Stat 22 (2004): 367-381.

Google Scholar, Crossref

4. Huang, Yu Chuan and Bor-Jing Lin. "Value-at-risk analysis for Taiwan stock index futures: Fat tails and conditional asymmetries in return innovations." Rev Quant Fin Acct 22 (2004): 79-95.

Google Scholar, Crossref

5. Bams, Dennis, Thorsten Lehnert and Christian CP Wolff. "An evaluation framework for alternative VaR-models." J Int Money Fin 24 (2005): 944-958.

Google Scholar, Crossref

6. Ané, Thierry. "An analysis of the flexibility of asymmetric power GARCH models." Comput Stat Data Anal 51 (2006): 1293-1311.

Google Scholar, Crossref

7. Angelidis, Timotheos, Alexandros Benos and Stavros Degiannakis. "The use of GARCH models in VaR estimation." Stat Methodol 1 (2004): 105-128.

Google Scholar, Crossref

8. Marcucci, Juri. "Forecasting stock market volatility with regime-switching GARCH models." Stud Nonlinear Dyn Econ 9 (2005).

Google Scholar, Crossref

9. Su, Ender and Thomas W. Knowles. "Asian pacific stock market volatility modeling and value at risk analysis." Emerg Mark Fin Trade 42 (2006): 18-62.

Google Scholar, Crossref

10. Brooks, Chris and Gita Persand. "Volatility forecasting for risk management." Int J Forecast 22 (2003): 1-22.

Google Scholar, Crossref

11. Giot, Pierre and Sébastien Laurent. "Value‐at‐risk for long and short trading positions." J Appl Econom 18 (2003): 641-663.

Google Scholar, Crossref

12. Diamandis, Panayiotis F. and Anastassios A. Drakos. "Financial liberalization, exchange rates and stock prices: Exogenous shocks in four Latin America countries." J Policy Model 33 (2011): 381-394.

Google Scholar, Crossref

13. Neftci, Salih N. "Value at risk calculations, extreme events and tail estimation." J Deriv 7 (2000): 23-37.

Google Scholar, Crossref

14. Omari, Cyprian O., Peter N. Mwita and Antony G. Waititu. “Using conditional extreme value theory to estimate value-at-risk for daily currency exchange rates.” Appl Math Fin (2017): 846-870.

Google Scholar, Crossref

15. Longin, Francois M. "From value at risk to stress testing: The extreme value approach." J Bank Financ 24 (2000): 1097-1130.

Google Scholar, Crossref

16. Hung, Jui-Cheng, Ming-Chih Lee and Hung-Chun Liu. "Estimation of value-at-risk for energy commodities via fat-tailed GARCH models." Energy Econ 30 (2008): 1173-1191.

Google Scholar, Crossref

17. Carvalhal, Andre and Beatriz VM Mendes. "Value-at-risk and extreme returns in Asian stock markets." J Int Bus Stud 8 (2003).

Google Scholar, Crossref

18. Gilli, Manfred, Evis Këllezi and Hilda Hysi. "A data-driven optimization heuristic for downside risk minimization." J Risk Res 6 (2006).

Google Scholar, Crossref

19. Cotter, John. "Modelling catastrophic risk in international equity markets: An extreme value approach." Appl Econ Lett 2 (2006): 13-17.

Google Scholar, Crossref

20. Aggarwal, Raj and Min Qi. "Distribution of extreme changes in Asian currencies: tail index estimates and value-at-risk calculations." Appl Financial Econ 19 (2009): 1083-1102.

Google Scholar, Crossref

21. De Jesús, Raúl and Edgar Ortiz. "Risk in emerging stock markets from Brazil and Mexico: Extreme value theory and alternative value at risk models." Front Financ Econ 8 (2011): 49-88.
22. De Jesús, Raúl, Edgar Ortiz and Alejandra Cabello. "Long run peso/dollar exchange rates and extreme value behavior: Value at Risk modeling." North Am J Econ Finance 24 (2013): 139-152.

Google Scholar, Crossref

23. Gencay, Ramazan and Faruk Selçuk. "Extreme value theory and value-at-risk: Relative performance in emerging markets." Int J Forecast 20 (2004): 287-303.

Google Scholar, Crossref

24. Mutu, Simona, Peter Balogh and Darie Moldovan. "The efficiency of value at risk models on central and eastern European stock markets." Int J Math Comput Simul 5 (2011): 110-117.

Google Scholar, Crossref

25. Kittiakarasakun, Jullavut and Yiuman Tse. "Modeling the fat tails in Asian stock markets." Int Rev Econ Finance 20 (2011): 430-440.

Google Scholar, Crossref

26. McNeil, Alexander and Rüdiger Frey. "Estimation of tail-related risk measures for heteroscedastic financial time series: an extreme value approach." J Empir Finance 7 (2000): 271-300.

Google Scholar, Crossref

27. Fernandez, Viviana. "Risk management under extreme events." Int Rev Financial Anal 14 (2005): 113-148.

Google Scholar, Crossref

28. Danielsson, Jon. Financial Risk Forecasting. UK, (2011).
29. McNeil, Alexander "Extreme value theory for risk managers." Departement Mathematik ETH Zentrum 12 (1999): 217-37.

Google Scholar, Crossref

30. Cotter, John. "Tail behaviour of the euro." Appl Econ 37 (2005): 827-840.

Google Scholar, Crossref

31. Ghorbel, Ahmed and Abdelwahed Trabelsi. "Predictive performance of conditional extreme value theory in value-at-risk estimation." Int J Monet Econ Finance 1 (2008): 121-148.

Google Scholar, Crossref

32. Karmakar, Madhusudan. "Estimation of tail-related risk measures in the Indian stock market: An extreme value approach." Annu Rev Financial Econ 22 (2013): 79-85.

Google Scholar, Crossref

33. Mögel, Benjamin and Benjamin R. Auer. "How accurate are modern value-at-risk estimators derived from extreme value theory?." Rev Quant Fin Acct 50 (2018): 979-1030.

Google Scholar, Crossref