Construction of Right Cheban Loops of Small Order

AI Chinaka^1*, AO Abdulkareem² and JO Adenıran^1
*Correspondence: AI Chinaka, Department of Mathematics, Federal University of Agriculture, Abeokuta, Nigeria, Tel: 2348063718542, Email:

Keywords

Binary operations • Construction of loops • Right cheban loop

Introduction

Right cheban loops are loops of generalized bol-moufang type. Both left cheban loops and cheban loops were introduced by cheban. He also showed that cheban loops are generalized moufang loops. Phillips and Shcherbacov also carried out a study on the structural properties of left cheban loops and cheban loops [1-3].

The smallest Bol-loops surfaced as from order 8. This was classified by Burn in [4,5]. He found six Bol-loops of order 8. Later, solarin and sharma, using a different method classified Bol-loops of orders 12, 16, 32 and generally of order 3p (p>3) where p is prime. At order twelve we begin to have moufang loops. The least Moufang loop is of order twelve and there are just three of such loops. This was classified by orin and pflugfelder in [6,7]. and osborn loops begin to surface as from order 16 and only two examples exist at that order. This was classified by kinyon in [8,9]. Some recent studies on this class of loops are by Isere Adeniran and Isere, et al, Jaiyeola, Jaiyeola and Adeniran. Solarin and Sharma, constructed some. examples of bol loops in. isere in also constructed and classified finite non-universal osborn loops of order 4n [10-12].

In this study, we give constructions of right cheban loops of order 4t, with the cartesian product of (C_2t х C₂) where C2t is a cyclic group of order 2t, t is a positive integer and C₂ is a cyclic group of order two (with element 0 and 1), each gives a right cheban loop of orders 12,16 and 24.

Preliminaries

Let Q be a non-empty set. Define a binary operation · on Q. If x · y ∈ Q for all x, y ∈ Q, then the pair (Q, ·) is called a groupoid. If the equations:

a · x=b and y · a=b

have unique solutions in Q for x and y respectively, then (Q, ·) is called a quasigroup. If there exist a unique element e ∈ Q called the identity element such that for all x ∈ Q

x · e=e · x=x

(Q, ·) is called a loop. Let x be a fixed element in a groupoid (Q, ·). The left and right translation maps of Q, Lx and Rx are respectively defined by

yLx=x · y and yRx=y · x

Also, a quasigroup is a groupoid in which the left and right translations defined on the groupoids are bijections. Since left and right translation mappings of a loop are bijectives

then, the inverse mappings L_x⁻¹ and R_x⁻¹ exist. Let

and note that

x\y=yL_x^{− 1}and y/x=yR_x^{− 1}

x\y=z ⇐⇒ x · z=y and x/y=z ⇐⇒ z · y=x.

A loop (Q, ·, \./, e) is a set Q together with three binary operations

(.)(/)(\) one nullary operation e such that

(i) x · (x\y)=y, (y/x) · x=y ∀x, y ∈ Q x

\(x · y)=y, (y · x)/x=y ∀x, y ∈ Q and

x\x=y/y or e · x=x and x · e=x ∀x, y ∈ Q

A loop satisfying the identity

(z · yx)x=zx · xy (1)

Is called a Right Cheban loop (RChL). left cheban loops on the other hand are loops satisfying the mirror identity

x(xy · z)=yx · xz (2)

Loops that are both right and left cheban are called cheban loops. cheban loops can also be characterized as those loops that satisfy the identity

x(xy · z)=(y · zx)x (3)

A loop (Q, ·) is called a right inverse property loop if it satisfies the right inverse property (RIP) given by:

(yx)x^ρ=y

A loop (Q, ·) is called a Right Alternative Property Loop (RAPL) if it satisfies right alternative property (RAP): yx · x=y · xx

satisfies right alternative property (RAP): yx · x=y · xx A loop (Q, ·) is called a left alternative property loop (LAPL) if it satisfies left alternative property (LAP): xx · y=x · xy

A loop (Q, ·) is called an alternative property loop (APL) if it is a RAPL and a LAPL.

A loop (Q, ·) is called a flexible loop if it satisfies the identity

xy · x=x · yx

for all x, y ∈ Q.

A loop (Q, ·) is commutative if L(a)=R(a) ∀ a ∈ Q and associative if

R(a, b)=R(a)R(b) a, b ∈ Q

A loop Q satisfying the identity

(xy · z)y = x(yz · y) (4)

is a Right Bol loop.

If it satisfies the identity it is called a left bol loop.

x(y · xz)=(x · yx)z (5)

A Loop (Q, ·) is moufang if it satisfies the identities 4 and 5 called the right and left Bol Loops respectively.

A loop I(·) is called an osborn loop [13-22], if it obeys the identity:

(x^λ\y) · zx=x(yz · x)

∀x, y, z ∈ I.

A Loop (Q, ·) is power associative if and only if each element generates an associative subloop.

A Loop (Q, ·) is diassociative if and only if pair of elements generates associative subloop.

Bruck defined the left nucleus Nλ , the middle nucleus N μ and the right nucleus Nρ of a loop (Q, ·) as follows:

Results

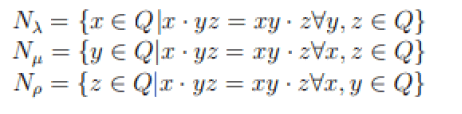
Construction (1): Let Q (◦)=C_2t х C₂ and the binary operation is defined as follows:

(x^β1, a^α1 )(x^β2, e)=(x^β1+^β2, a^α1 )

then Q (◦) is a right cheban loop of order 4t, where t=3,4,6.

Proof. Showing that Q◦ )( satisfies right cheban identity below, (MNP )P=MP PN

(a) M=(x^β1,e); N=(x^β2,e); P=(x^β3,e), then by direct computations we have,

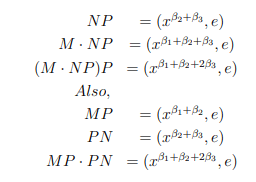
∴ (M · NP)P=MP · P N

ln the above computation (Q, ) = C_2t × C ₂ and the binary operation is defined as follows: (x^β1 , a^α1 )(x^β2 , e) = (x^{β1 +β2} , a^α1 )

(b) M = (x^β1 , e); N = (x^β2 , e); P = (x^β3 , a) then

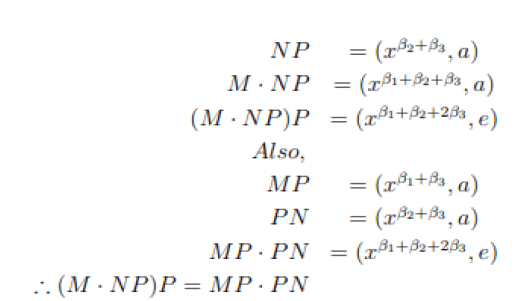
(c) M=(x^β1, e); N=(x^β2, a); P=(x^β3, e) then

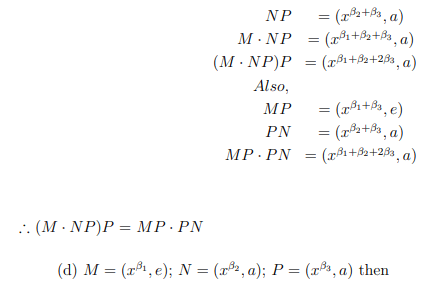
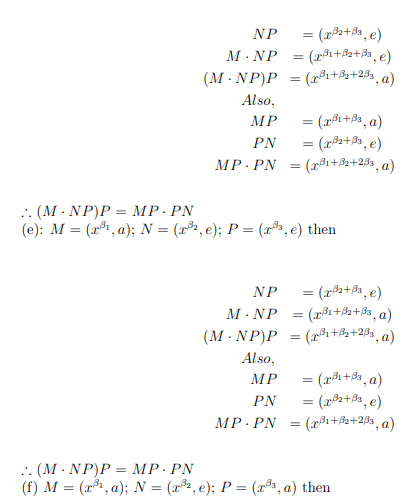
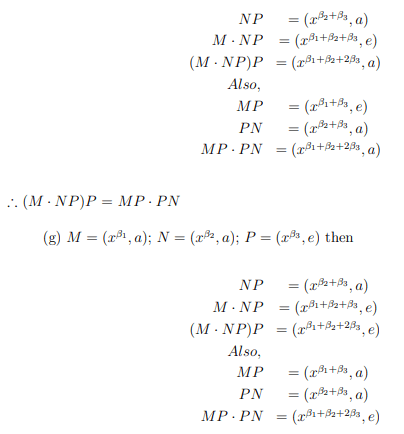
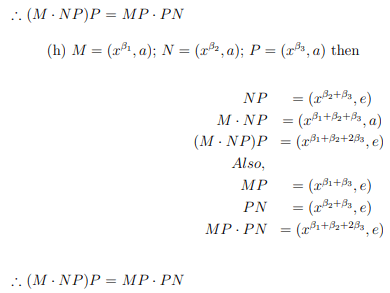
Also, (e, e) is the two sided identity.

If A=(x^β, e), then A⁻¹=(x^−β, e)

If A=(x^β, a), then

A⁻¹=(x^−β, a) if β=even

=(x−5^β, a) if β=odd therefore, the inverses are defined.

Also, for non-associativity, let M=(x^β1, a); N=(x^β2, a); P= (x^β3, e) where β2 and β3

are odd integers, then

MN·P=(x^β1+5^β2+5^β3, a) and

M·NP=(x^β1+5^β2+25^β3, a)

MN·P=M·NP

thus the construction is non-associative except when t=2 which gives the group C₄ х C₂

hence, it is a right Cheban loop of order 4t, t=3, 4, 6.

Since (zyx)x=zx xy holds in cases whenever 251 (mod 2t), that is t=3, 4, 6 hence, the construction is a right cheban loops of order 4t where t=3, 4, 6 see solarin and sharma [23-25].

Construction (2): Let Q(◦)=C_2t х C₂ and the binary operation is defined as follows:

(x^β1, aα1 )(x^β2, a) = (x^β1+^β2, aα1+1) if β₂ ≡ 0 (mod 2)

=(x5^β1+^β2, aα1+1) if β₂ ≡ 1 (mod 2) then

Q (^o) is a Right Cheban loop of order 4t, where t=3, 4, 6.

Proof to show that the LHS and RHS of right cheban identity are satisfied, we proceed, by considering different possible situations, as follows

M=(x^β1, e); N=(x^β2, e); P=(x^β3, e) then by direct computations we have,

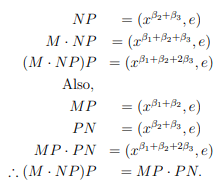
(b)M=(x^β1, e); N=(x^β2, e); P=(x^β3, a) then

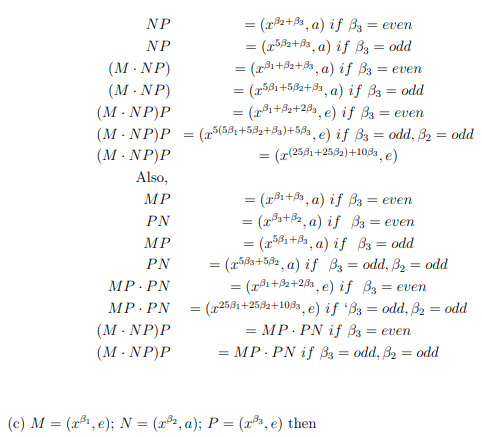
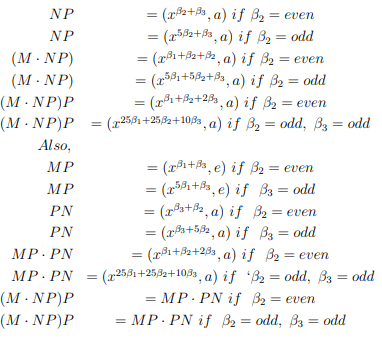
(d)M=(x^β1, e); N=(x^β2, a); P=(x^β3, a) then

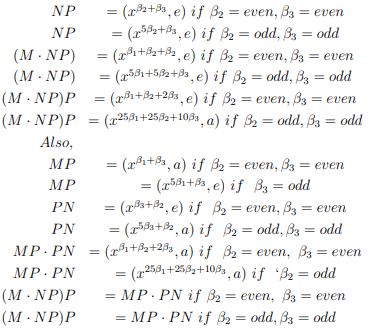
(e) M=(x ^β1, a); N=(x ^β2, e); P=(x ^β3, e) then

NP=(x^β2+^β3, e)

M · NP=(x^β1+^β2+^β3, a)

(M · NP )P=(x^β1+^β2+2^β3, a)

Also,

MP =(x^1β+^β2, a)

PN=(x^β2+^β3, e) MP ·

PN=(x^β1+^β2+2^β3, a)

(M · NP )P=MP · PN

(f) M=(x^β1, a); N=(x^β2, e); P=(x^β3, a)

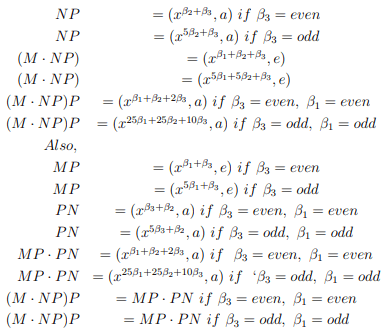
(g) M=(x^β1, a); N=(x^β2, a); P=(x^β3, e)

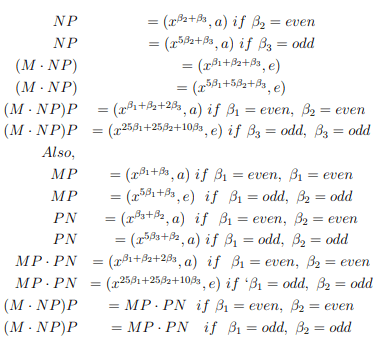
(h) M=(x^β1, a); N=(x^β2, a); P=(x^β3, a)

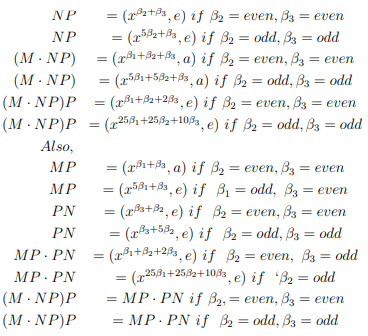
Also, (e, e) is the two sided identity. If A=(x^β, e), then A⁻¹=(x^−β, e) If A=(x^β, a), then

A⁻¹=(x^−β, a) if β=even

=(x^−5β, a) if β=odd therefore, the inverses are defined.

Also, for non-associativity, let M = (x^β1, a); N = (x^β2, a); P = (x^β3, e) where β2 is an even integer and β3 is an odd integer, then

MN · P=(x^β1+5^β2+5^β3, a) and

M · NP=(x^β1+5^β2+25^β3, a)

MN · P ≠ M · NP

Thus the construction is non-associative except when t=2 which gives the group C₄ х C ₂ hence, it is a right cheban loop of order 4t, t=3, 4, 6.

Cayley of non-associative right cheban loops of orders 12, 16 and 24.

These are non-associative right cheban loops of order 12, 16 and 24. From the constructions, it was found that the smallest non associative right cheban loops is of order 12 and using Group Algorithm Programmings Software (GAPS), it was shown that right cheban loops are right inverse property loops, right conjugacy closed, power associative, right bol loops, right alternative and non-moufang loop, non-osborn loop, not diassociative loop and does not satisfy flexibility law and commutativity law.

References

1. Adeniran JO and Solarin ART. A note on generalised Bol identity. Scientific Annal of AII Cuza Univ 45 (1999): 99-102.

2. Adeniran JO and Isere AO. Nuclear Automorphisms of a class of Osborn Loops. J Niger Soc Math Biol 22 (2012): 5-8.

3. Bruck RH. A Survey of Binary Systems, Springer-Verlag, Berlin- Gottingen-Heidelbreg. Burn, R. P. (1978), Finite Bol loops. Math Proc Camb Phil Soc 84 (1958): 377-385.

4. Burn RP. Finite Bol loops II. Math Proc Camb Phil Soc 88 (1981): 445-455.

5. Chein O, Pflugfelder HO, Smith JDH. Quasigroups and loops: theory and applications. helsermann Verlag. 1990: 568.

6. Cote B, Harvill B, Huhn M and Kirchman A. Classification of loops of generalized Bol-Moufang type. Quasigroups and Related Systems 19 (2011): 193-206.

7. Drapal A and Jedlicka P. On loops identities that can be obtained by a nuclear identification. European J Combin 31 (2010): 1907-1923.

   [Crossref][Googlescholar]

8. Isere AO, Adeniran JO and Solarin ART. Some examples of finite Osborn loops. J Niger Soc Math 31 (2012): 91-106.

   [Googlescholar]

9. Isere AO.  Construction and classification of finite non-universal Osborn loops of order 4n, Ph.D Thesis, Federal University of Agriculture, Abeokuta, Nigeria. (2014).

10. Lsere AO, Adeniran JO and Jaiyeola TG. Holomorphy of osborn loops. Analele Univesitatii de Vest, Timisoara Seria Matematica-lnformatica LIII 2 (2015): 81-98.

    [Crossref][Googlescholar]

11. Isere AO, Adeniran JO and Jaiyeola TG. Generalized Osborn Loops of Order 4n. Acta Universitatis Apulensis. Maths inform 43 (2015): 19-31.

12. Isere AO, Adeniran JO and Agboola AAA. Representations of Finite Osborn Loops. J Niger Soc Math Biol 35 (2016): 381-389.

    [Googlescholar]

13. lsere AO, Adeniran JO and Jaiyeola TG. Classification of Osoborn loops of order 4n. Proyeociones J M Univer Catolica del Norte Antofagasta-Chile 38 (2019): 31-47.

14. Jaiyeola TG. The study of the universality of Osborn loops, Ph.D Thesis, University of Agriculture, Abeokuta Ogun State, Nigeria. (2008).

15. Jaiyeola TG and Adeniran JO. New identities in universal Osborn loops. Quasigroups and Related Systems 17 (2009): 55-76.

    [Crossref][Googlescholar]

16. Jaiyeola TG. Osborn loops and their universality. Scientific Annals of AI.I. Cuza University of lasi, Tomul LVIII. (2012).

17. Jaiyeola TG.  New identities in universal Osborn loops II, Algebras, Quasigroups And Related Systems 30 (2013): 111-126.

    [Crossref]

18. Jaiyeola TG and Adeniran JO. Not every Osborn loop is universal. Acta Mathematica Academiae Paed agogiace Nyregyhziensis 25 (2019): 189-190.

19. Kinyon MK. A survey of Osborn loops, Mile High Conference on loops, quasigroups and non-associative system. university of Denver, Denver Colorado (2005).

20. Orin C and Plugfelder HO. On maps x xn and the isotopy-isomorphy property of Moufang. Aequ Math 6 (2005): 157-161.

    [Googlescholar]

21. Osborn JM. Loops with the weak inverse property. Pac J Math 10 (1961): 295–304.

    [Googlescholar]

22. Pflugfelder HO. Quasigroups and Loops: Introduction. Sigma series in Pure Math. 7, Heldermann Verlag, Berlin. (1990): 147.

23. Philips JD and Shcherbacov VA. Cheban Loops. J Generalized Lie Theory App 4 (2010): 1-5.

    [Crossref][Googlescholar]

24. Sharma BL and Solarin ART. On the classification of Bol loops of order 3p (p>3). Commun Algebra 16 (1988): 37-55.

    [Crossref][Googlescholar]

25. Solarin ART and Sharma BL. Some examples of Bol Loops, ACTA Universitatis Carolinae. Mathematica et Physica 25 (1984): 59-68.

    [Googlescholar]