Research Article - (2025) Volume 14, Issue 1
Received: 20-Jul-2024, Manuscript No. JACM-24-142652;
Editor assigned: 23-Jul-2024, Pre QC No. JACM-24-142652 (PQ);
Reviewed: 06-Aug-2024, QC No. JACM-24-142652;
Revised: 06-Feb-2025, Manuscript No. JACM-24-142652 (R);
Published:
13-Feb-2025
, DOI: 10.37421/2168-9679.2025.14.600
Citation: Ramanuja, Mani, Vishwanath Savanur, Y. Rajesh Yadav, B. Srikantha Settee, A. Rushi Kesava. "Comparative Study on MHD Flow of Casson Fluid due to Stretching Surface in Suspension of Dust Graphene Nanoparticles: Entropy Generation." J Appl Computat Math 14 (2025): 600.
Copyright: © 2025 Ramanuja M, et al. This is an open-access article distributed under the terms of the creative commons attribution license which permits unrstricted use, distribution and reproduction in any medium, provided the original author and source are credited.
This study investigates the effects of the MHD flow via an exponentially extending surface of a Casson hybrid nanofluid made of graphene and carbon nanotubes with basic Casson fluid. The directions of flow were subjected to the standard Lorentz force. The velocity, temperature and concentration profiles are simulated using a mathematical model established under the flow suppositions by utilizing boundary exponentially layer surface approximations in equations using Partial Differentials (PDEs). The lie symmetry method was used to achieve a suitable performance of mathematical transformations. After applying the necessary transformations, Partial Differential Equations (PDEs) were transformed into Ordinary Differential Equations (ODEs). The dimensionless system was explained using a numerical with 4th-order Runge–Kutta method called bvp4c. Both tabular and depicted graphical representations were used to show the influence of relevant flow parameters on skin friction, Nusselt number, velocity, temperature and concentration distributions. Furthermore, the Casson fluid parameter, magnetic field strength, Brownian motion, random motion, volume fraction and radiation parameter cause the temperature profiles to rise at the surface can be observed. Also, increasing with Brownian motion, thermophoretic parameter and radiation parameter increases the primary velocity while decreasing with Casson fluid parameter and magnetic field parameter. Furthermore, insight into system irreversibility and demonstrates actual system transit from a low entropy configuration to a high entropy configuration.
MHD • Casson fluid • CNT • Graphene • Hybrid nanofluid • Stretching sheet
A Casson fluid is a non-Newtonian fluid that exhibits both shearthinning behaviour and yield stress. Unlike Newtonian fluids, where viscosity remains constant regardless of shear rate, Casson fluids show a decrease in viscosity with increasing shear rate. Additionally, they have a minimum shear stress, known as yield stress. Casson fluids are commonly encountered in various industrial applications, such as food processing, pharmaceuticals and paints. This study desires to analyze the heat and mass transmission in a Casson hybrid nanofluid flow across an exponentially stretched sheet. Numerous excellent substitutes for armory manufacturing and heat exchange performance are the combination of CNT and graphene nanoparticles because of their exceptional characteristic ratio, heat and electrical conductivity and lightweight nature. It was demonstrated that the Casson hybrid nanofluid's rates are superior to those of the individual nanofluids. CNTs and graphene nanoparticles have garnered significant interest for their unique properties and potential applications. Investigators continue to explore ways to harness these materials for various technological advancements, ranging from nano electronics to materials science and medical applications. Also, combining CNTs and graphene, hybrid materials are being researched for synergistic effects in terms of properties and applications. The heat transfer velocity is one of the most crucial characteristics of hybrid nanofluid flow that may be examined. It is envisaged that the combination of these two unique materials will enhance heat transfer in the flow of the electrically conducting Casson hybrid nanofluid.
Hamad et al. examined boundary-layer fluid flow and heat transfer across a vertically stretched sheet of a power-law non-Newtonian nanofluid [1,2]. Bachok et al. has focused on the boundary-layer fluid flow of a nanofluid in a uniform free stream past a moving semi-infinite flat plate [3]. Nadeem and Lee examined the analytical research done on the stable boundary layer of nanofluid flow over an exponential stretching surface [4]. Sundar et al. have reports show that nanofluids are valuable heat transfer fluids for engineering applications and there has been a sharp rise in research on this topic. A novel class of nanofluids known as hybrid nanofluids was described, one that could find use in nearly every area of heat transmission by Minea et al. [5,6]. Ghosh and Mukhopadhyay investigated the non-Newtonian fluid behavior that was characterized by operating the Casson fluid model [7]. Rasool et al. intends to talk about the properties of a Casson-type nanofluid that is kept in motion to flow through a permeable media across a non-linear stretching surface from the standpoint of advancements in mass and heat transmission [8]. Krishna et al. explored the effects of ion slip, chemical reaction, radiation absorption and hall on unstable magnetohydrodynamics an incompressible viscous, electrically conducting, heat-generating and absorbing fluid in a rotating frame with a semi-infinite porous plate encircling it has been designed for MHD-free convective laminar flow [9,10]. Guedri et al. have investigated micropolar fluids, with their distinct microstructures and have garnered significant interest in the industrial domain for their potential uses in mass and convective polymer manufacturing, as well as in the stiff and random cooling of metallic sheet particles. Moreover, Sneha et al. inspected the current analysis looks into heat transfer on non-Newtonian fluid flows through a stretching/shrinking sheet and tilted Magnetohydrodynamics (MHD).
Eid et al. examined the thermal characteristics of non-Darcian MHD rotating hybridity nanofluid thin film flow. Li et al. explored the slip effect on a 3D bioconvection flow of the Casson nanofluid in a rotating frame via a homotopy analysis mechanism. Mani et al. examined the chemically reactive nanofluid glowing across horizontal cylinders using the numerical solution. Naresh et al. explored the Jeffrey nanofluid over a stretching sheet considering melting heat transfer and viscous flowers.
Investigate hybrid numerical methods that combine the strengths of different approaches, such as RK methods to handle complex problems more effectively. Hybrid methods can leverage the advantages of each approach while mitigating their limitations.
This is because your future research suggestions generally arise from the research limitations you identified in your dissertation. In this article, we discuss types of future research suggestions. These include different nanoparticles, base fluids, porous mediums, and physical parameters.
This work explores the MHD flow via behavior of an exponentially stretching surface of a Casson hybrid nanofluid composed of CNTs and graphene. The similarity variables are exploited to illustrate and non-dimensionalize the flow of a hybrid Casson nanofluid. Ordinary Differential Equations (ODEs) are created by converting Partial Differential Equations (PDEs). Next, we use the fifth-order RungeKutta method to analyze the Ordinary Differential Equations (ODEs). We also examine the impact of the physical characteristics, which are evaluated visually. Numerical outcomes are displayed in tables. These are original findings that could have applications in industry and engineering. An analysis and discussion are executed on the result of relevant parameters on the flow's concentration, temperature and velocity.
Formation of the problem
The rheological equation of condition is as follows for a Casson fluid's isotropic and incompressible fluid flow.
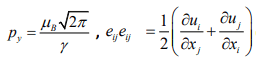
(Rate of strain tenor), π=eijeij and is the (i, j)th component of deformation rate, model, γ Casson parameter, n is the product of deformation rate with itself, πc is a critical value of this product based on the non-Newtonian, μB+PY/√2π is the plastic dynamic viscosity of the non-Newtonian fluid and y p is the yield stress of the fluid.
For mathematical modeling, we consider that the fluid flow is steady, electrically conducting and incompressible 2-dimensional ginduced gravity due to acceleration and the no-slip situation is considered. A magnetic field of constant force is also utilized in the transverse direction. Thus, the fluid layers next to the wall have the property of exponential stretching of the surface in the x-axis direction, through the same bending velocity u|=U0e x/L, here L be the characteristic length, we used a Casson base fluid for this investigation to suspend graphene and CNT nanoparticles. The subsequent hybrid nanofluid traverses a surface. Figure 1 shows how the flow is physically configured.
Figure 1. Physical model representing flow configuration.
Below is the set of leading equations of motion under the previously indicated approximations. Equations controlling the flow of a Casson hybrid nanofluid through an exponential stretching surface in the occurrence of thermal radiation are found in, where the Buongiorno model is adopted to correct the dimensionless units.
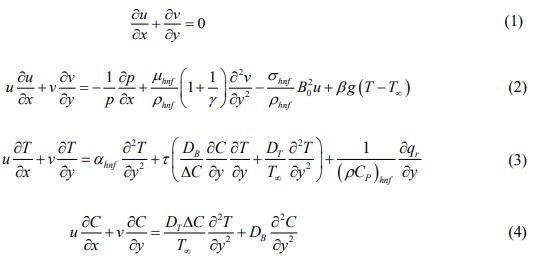
Here u and v represents the velocity details in x and y direction. T be the temperature, C be the concentration, u and µ be the dynamic and kinematic viscosity, σ is the electric conductivity coefficient, g is the acceleration due to gravity, B0 be the magnetic field strength, DT and be the thermophoretic and Brownian diffusivity, β be the thermal expansion coefficient, ρ be the density coefficient, CP be the specific heat capacity, γ is the Casson fluid, f be the base Casson fluid and be the hybrid nanofluid. The related boundary limits of this model to initial condition and no-slip boundary are:
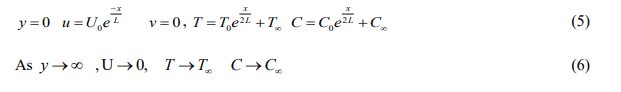
Brewster has the following appearance by providing a less radiative heat flow than Roseland's approximation.

Here k* be the indicate absorption coefficient, on T0 reference temperature T4 term and avoid the higher power situations as part of Taylor’s series, σ * is the ‘‘Stefan-Boltzmann’’, therefore getting higher T 4 .

When equation (7) is explored, equation (8) has the following form

Using equations (3) and (9) the equation becomes
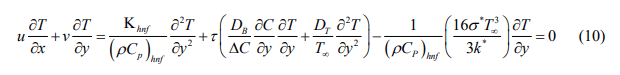
The dimensionless variables indicated below are being used:
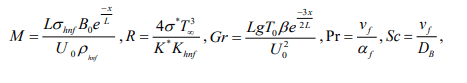

The governing Eqs (2), (4) and (11) then exploiting the transformation along with the boundary conditions (5)-(6) becomes
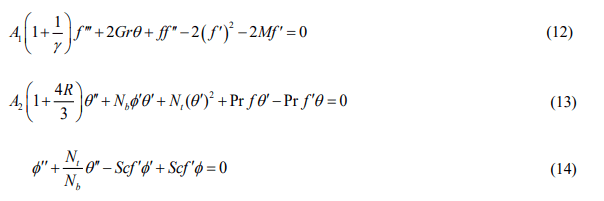
Here Gr be the Grashof number, Pr be the Prandtl number, γ be the Casson fluid parameter, f’ dimensionless velocity, M be the magnetic parameter, Nt be the thermophoretic parameter, Nb Brownian motion parameter, θ be the dimensionless temperature, φ be the dimensionless concentration, Sc be the Schmidt number. R be the Radiation parameter (Tables 1 and 2).

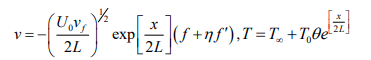
The values of practical concern are skin friction coefficient, Nusselt number and Sherwood number, which stand expressed as
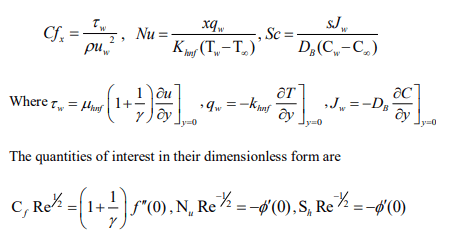
| Quantities | Hybrid nanofluid |
| Thermal diffusivity | 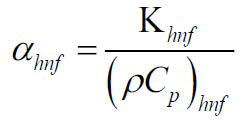 |
| Density | 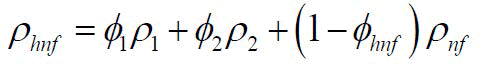 |
| Viscosity | 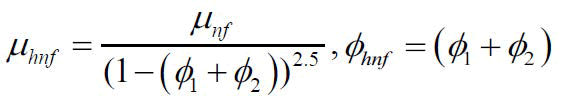 |
| Heat capacity | 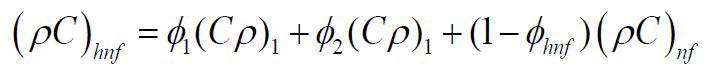 |
| Electrical conductivity | 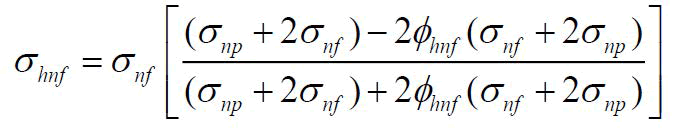 |
| Volumetric expansion coefficient for hybrid nanofluid | 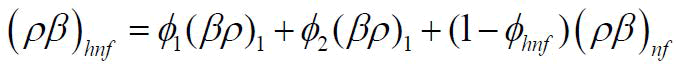 |
Table 1. Physical and thermal characteristics of the hybrid nanofluid.
The base fluid's density, viscosity, thermal expansion coefficient, thermal diffusivity, heat conductivity and electrical conductivity are listed in that order. Additionally, 1 and 2 refer respectively to the nanoparticle.
| Physical properties | Nanoparticles | |
| Graphene | SWCNT | |
| cp (J/kg K) | 2100 | 425 |
| ρ (kg/m3) | 2250 | 2600 |
| K (w/mK) | 2500 | 6600 |
Table 2. Thermophysical characteristics of base fluid and nanoparticles.
Solution of the problem
The current linear (ODE’s) Eqs (12) to (14) when used in combination with the boundary conditions (15)-(16), relating to the (BVP) boundary value problem. Because a precise solution to these equations is impossible, we have opted to cross suggested meant for a numerical explanation by lowering the linear (BVP) to (IVP) an initial value issue. The IVP is solved by utilizing the 4th- order Runge-Kutta procedure in such a situation. The dimensionless boundary value problem above is converted to its equivalent starting value problem in this research using the shooting technique. Rewriting the dimensionless equations as a system of first order ODE’s we have
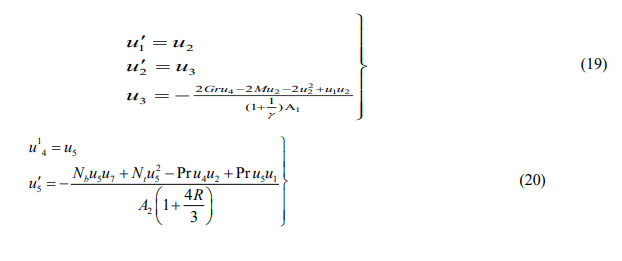
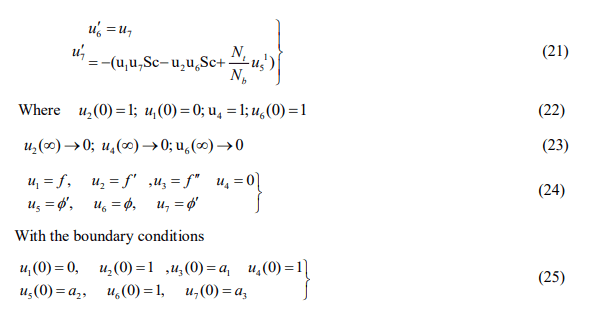
Solve the system of equations with some initial guesses for a1, a2 a3 and the results are compared with the three free stream conditions.
Entropy generation analysis
The entropy generation study provides insight into system irreversibility and demonstrates actual system transit from a low entropy configuration to a high entropy configuration. Bejan number Be is defined by Be=Sh/Sh+Sf , which is a parameter of the irreversibility distribution that quantifies NS=Sh+Sf , here Sh entropy be produced here Sh entropy be produce by heat transfer and Sf denotes the entropy induced by frictional forces in a fluid. The following is the local entropy production rate per unit volume for a conducting fluid.
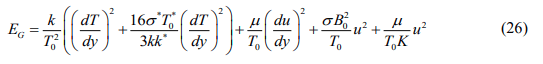
In dimensionless terms the following formula can be used to calculate the entropy generating quantity.
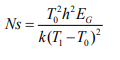
Making use of the dimensionless variables defined in (26), the equations (27) assume the following form
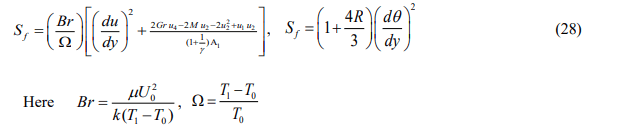
These characteristics are usually present in issues involving second law analysis. In most applications we find â?¦ ≤ 1.
Numerical impacts for this work explore the MHD flow via an exponential stretching surface of a hybrid nanofluid composed of CNTs and graphene. Numerical computations have been run to study the effect of flow characteristics corresponding to different flowinducing parameters. The current linear (ODE’s) Eqs (19) and (23), when used in combination with the boundary conditions (24)-(25), solved by utilizing the 4th-order Runge-Kutta procedure in such a situation. Investigation and discussion are executed on the effect of suitable parameters on the flow's velocity profile, temperature profile and concentration profile are depicted graphically. The flow inducing parameters held fixed were.
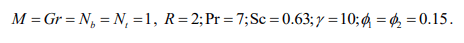
Figures (2) to (5) illustrate how the different dimensionless parameters affect the velocity profiles, figures (6) to (10) temperature profiles and figures (11) to (12) concentration profiles.
Figure 2 reveals the impact of velocity on variation values of the Casson parameter γ. Figure 2 illustrates how the primary rate decreases as the Casson fluid parameter (γ) increases. The viscous boundary layer thickness rises with the Casson fluid parameter (γ), increasing the viscous effects on the flow. The Lorentz force is an obstructing force created when a magnetic field is present in the flow field. Increases in the magnetic field strength imply a rise in the Lorentz force, which opposes fluid movement. This explains why the velocity profiles decrease as the strength of the magnetic field rises. According to the secondary Lorentz, drag force is truthfully positive and is assistive to secondary momentum development when the magnetic field is positive. Figure 3 indicates rate profiles for comparable values of the (M) magnetic parameter. The primary velocity decreases as the magnetic parameters (M) increase, as seen in Figure 3. The suspended nanoparticles collide with the expanding surface wall and each other repeatedly, increasing the flow's kinetic energy and consequently, the velocity profiles. This is evident from the relation that the reciprocal of magnetic Prandtl number is inversely proportional to momentum diffusivity, which is low near the stretching sheet.
Figure 2. Impact of velocity for variation γ.
Figure 3. Impact of velocity for variation M.
Figure 4 depicts the for-temperature profiles discrete values of Nb and Nt . The fluid particles are excited by the heat inflow, increasing the flow velocity. Due to increasing the Brownian motion, the kinetic energy increases, which results in the collision of atoms/molecules of the fluid; consequently, the net flow decreases.
Figure 4. Impact of velocity for variation Nb and N
Figure 5 depicts the effect of rate profiles for discrete values of radiation parameters R. Moreover, the flow's heat energy increases as the radiation parameter R is raised. The heat inflow excites the fluid particles, increasing the flow velocity. Therefore, the velocity profiles noticeably increase when the radiation parameter R is increased. The influence of radiation in the thermal boundary layer Eq. (10) is equivalent to an increased thermal diffusivity.
Figure 5. Impact of velocity for variation R.
Figures 6 and 7 depicted the temperature for dissimilar values of the Casson fluid parameter (γ) and Magnetic parameter (M). The fluid takes on Newtonian properties when the Casson fluid parameter approaches infinity. Therefore, raising the Casson fluid parameter forces the thermal boundary layer thickness to rise, forcing the temperature gradient to spike. This explains why, as seen in Figure 6, the temperature profile increases as the Casson fluid parameters improve. The temperature profile rises when the magnetic field parameter is increased, as Figure 7 illustrates. This effect can be explained by the fact that there is a great deal of internal friction between the fluid molecules in the thermal boundary layer expected to the Lorentz force generated by the magnetic field M. As the strength of the magnetic field M grows, heat is produced as more internal energy, raising the flow temperature profiles. A rise in the volume fraction causes the nanoparticles' surface region to grow, improving their thermal conductivity.
Figure 6. Impact of velocity for variation γ.
Figure 7. Impact of velocity for variation M.
Figures 8 and 9 depict the temperature for dissimilar values of the parameter refer respectively to the nanoparticle. As a result, Figure 8 illustrates how the temperature profile rises as the volume fraction does, as predicted. The rising thermal radiation is what causes the temperature profile in Figure 9 to rise, the collision rate among the nanoparticles increase which assists to grow in the heat generation. Against the magnetic field, the upsurge in temperature function is attributed to the dissipation in kinetic energy consumed in dragging the micropolar. In addition, the temperature is always supreme at the wall. This is because thermal radiation transfers better heat than any other parameter depicted before. In physical terms, the thermal conductivity of CNTs increases with the increase of the radiation parameter and as a result, the thermal boundary-layer thickness and the profiles of temperature increase.
Figure 8. Impact of velocity for variation Φ1 dna Φ2.
Figure 9. Impact of velocity for variation R.
Figures 10 and 12 depicted the temperature for dissimilar values of the influences of various parameters on the concentration profile. The impacts of the dimensionless parameters on the concentration are depicted in Figures 10-12. The concentration profile rises when the Casson parameter grows because the concentration at the boundary layer increases as seen in Figure 10. The Lorentz force is produced by increasing the magnetic field parameter and this causes the momentum barrier layer to thicken. Explains the relation between the concentration of nanoparticles and the magnetic parameter. The concentration of particles increases with the increasing values of the magnetic parameter. When the magnetic field is applied to the nanoparticles, dipoles of nanoparticles are formed. These are aligned in the direction of the same magnetic field and thus, the concentration of nanoparticles increases.
Consequently, Figure 11 depicts how the concentration profile rises as the magnetic parameters M increase, but the nanoparticle concentration profile reduces in the stagnation point region. Figure 12 displays how the concentration profile decreases as the radiation parameter R increases. This is because heat is produced in the flow as the radiation parameter R rises. Particle concentration within the boundary layer decreases as a result of enhanced nanoparticle migration from the boundary layer induced by a rise in flow temperature, but the nanoparticle concentration profile reduces in the stagnation point region.
Figure 10. Impact of velocity for variation γ.
Figure 11. Impact of velocity for variation M.
Figure 12. Impact of velocity for variation R.
Validation
Numerical impacts for this work explore the MHD flow via an exponentially stretching surface of a hybrid nanofluid composed of CNTs and graphene. Numerical computations have been run to study the effect of flow characteristics corresponding to several flowinducing parameters. Casson fluid past a continuously stretching surface under the influence of radiation, Prandtl number and magnetic field impacts were studied. To examine the flow behaviour of a hybrid nanofluid composed of CNTs and graphene for velocity and temperature profiles, a rigorous numerical computation was accomplished for numerous parameter values, which narrated the flow characteristics. Moreover, Table 3 is presented to establish a comparison with existing literature published work of two illustrates the current results of the proposed study and a good agreement was found, corroborating our work and that validates the convergence criteria of the present methodology adopted.
| M | R | Pr | Ref no | Present work |
| 0 | 0 | 0.5 | 0.5967 | 0.5964 |
| 0 | 0 | 1 | 0.9548 | 0.9549 |
| 0 | 0 | 2 | 1.4715 | 1.4715 |
| 1 | 0 | 1 | 0.8615 | 0.8616 |
| 1 | 1 | 1 | 0.462 | 0.4618 |
| 1 | 1 | 2.5 | 1.2016 | 1.2017 |
Table 3. Validation of results.
This analysis aimed to study the effects of the MHD flow via an exponentially stretching surface of a hybrid Casson nanofluid composed of CNTs and graphene. The similarity variables are exploited to depict and non-dimensionalize the flow of a hybrid Casson nanofluid. Numerical computations have been run to explore the influence of flow characteristics on dissimilar flow-effecting parameters. Analysis and discussion are executed on the influences of suitable parameters on the flow's velocity profile, temperature profile and concentration profile, which are depicted graphically. Some of the key findings are summarized below:
• Increasing with Brownian motion, thermophoretic parameter and radiation parameter increases the primary velocity while decreasing with Casson fluid parameter and magnetic field parameter.
• The Casson fluid parameter, magnetic field strength, Brownian motion, random motion, volume fraction and radiation parameter cause the temperature profiles to rise.
• The Casson parameter and the strength of the magnetic field cause a rise in the concentration profiles, but the radiation parameter causes a drop.
• In contrast to decreasing magnetic field strength and Prandtl number, the skin friction coefficient increases with Grashof number, Casson fluid parameter and radiation parameter.
• The Nusselt number is inversely correlated with the radiation parameter, Casson fluid parameter and magnetic field strength; it increases with the Grashof and Prandtl numbers.
• Sherwood number decreases with Casson fluid parameter, magnetic field strength and Prandtl number but increases with Grashof number and radiation parameter.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
[Google Scholar] [PubMed] [Crossref]
[Google Scholar] [PubMed] [Crossref]
Journal of Applied & Computational Mathematics received 1282 citations as per Google Scholar report