Research Article - (2020) Volume 14, Issue 2
Received: 03-Jun-2020
Published:
01-Jul-2020
, DOI: 10.37421/1736-4337.2020.14.300
Citation: Fadipe Joseph, Olubunmi A, Olanike R. Oluwaseyi, and O.E. Opaleye. “Coefficient Bounds of Functions over the Quaternions.” J Generalized Lie Theory Appl 14 (2020): 300. doi: 10.37421/GLTA.2020.14.300
Copyright: © 2020 Fadipe-Joseph OA, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which
permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
In this work, a new class of functions over the quaternions was defined. The initial coefficient bounds for the class defined were obtained. The work was concluded by establishing the Fekete-Szego˙ functional. AMS Mathematics Subject Classification (2010): 30C45, 30G45.
Quaternions • Chebyshev polynomials • Modified sigmoid function
Let a complex number z be defined as z = x + yi, where x,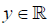 
and i2=-1. Let the quaternion field H be defined as
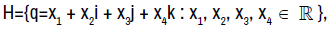
where the imaginary units i,j,k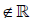 
satisfy
i2= j2= k2= −1, ij=−ji=k, jk=−kj=i, ki=−ik=j.
The quaternion extends the class of complex numbers. Recall that
Similarly,
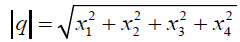
We denote by B the open unit ball centered at the origin in H, i.e.,
B={q ∈ H : |q| < 1} .
Let A be the class of functions of the form
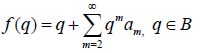
that are holomorphic in the open unit ball {B=q ∈H:|q| < 1} [1-4].
The theory of functions over the complex field is very rich. These functions are very useful in the analysis of practical problems of hydrodynamics, aerodynamics, elasticity, electrodynamics and the natural sciences. The quaternions are four dimensional. Therefore, it is important to study the geometric theory for quaternionic functions.
The Chebyshev polynomials of the first kind Tn(t), t[-1, 1] have the generating function of the form
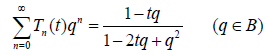
and that of second kind is :
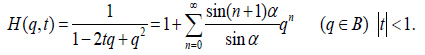
Note that if t = cosα, α ∈ ( −π/3 , π/3 ) then
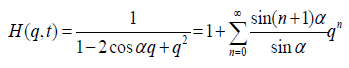
Thus,
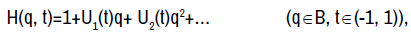
where
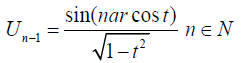
are the Chebyshev polynomials of the second kind. Also,
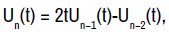
so that,
Lemma 1.1
If ω(q)=b1q+b2q2+b1≠0 is analytic and satisfy |ω(q)|<1 in the unit ball B, then for each 0<R<1, |ω’ (q)|<1 and ω(Reiθ)<1 unless ω(q) = eiσq for some real number σ
Lemma 1.2
Let ω ∈ Ω={ω ∈ A : |w(q)| ≤ |q| , q ∈ B}.
If ω ∈ Ω, ω(q) =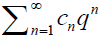 
(q ∈ B), then
|cn| ≤ 1 n = 1, 2, …. , |c2| ≤ 1 − |c1|2 (1.3)
and
(1.4)
The result is sharp. The functions
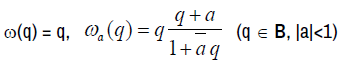
are extremal functions.
Definition 2.1
The modified sigmoid function is defined in series form as
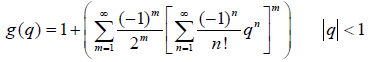[7]
Theorem 2.1
Let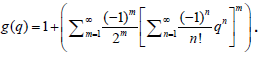 
Then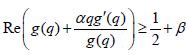 
for some real α ≥ 0;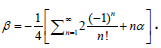 
Proof: By definition,
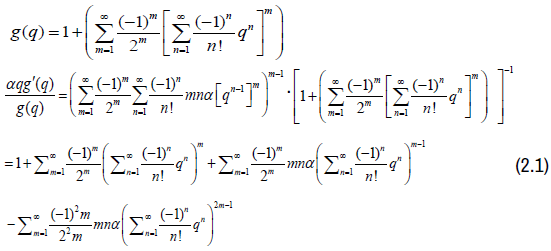
When m=1 in (2.1),
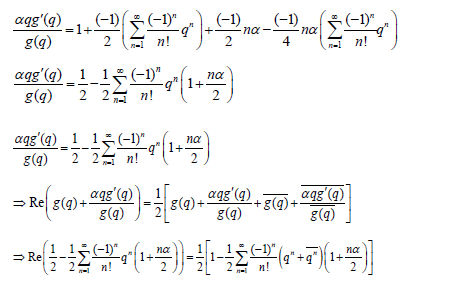
Since q = Reiθ,
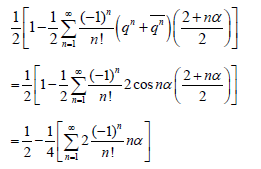
Hence,
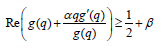
Where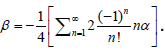 
Definition 2.2
A function f∈A is said to be in the class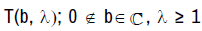 
if the following subordination holds.
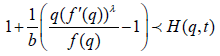
Theorem 2.2
If f (q) as defined in (1.1) belongs to the class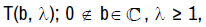 
then,
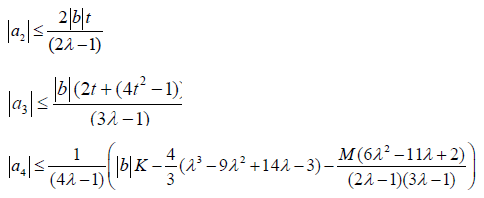
where
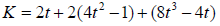
and
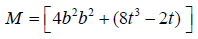
Proof: Suppose f ∈ T (b, λ), then by definition
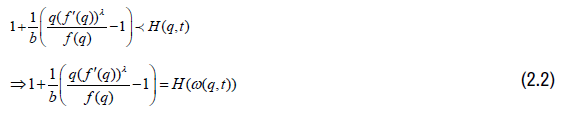
Now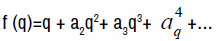 
and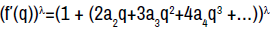 
Using binomial expansion,
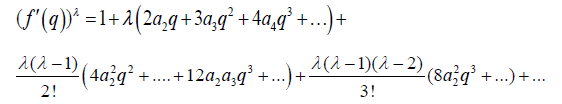
This implies that
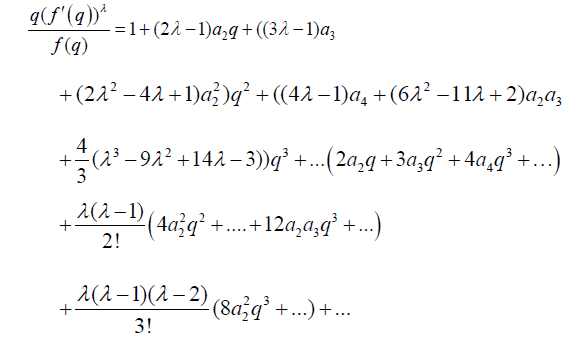
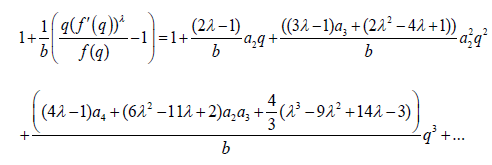(2.3)
Since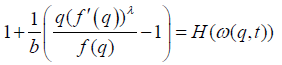 
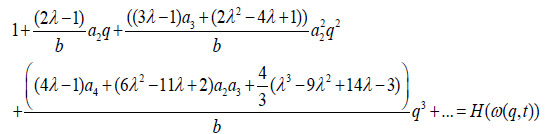
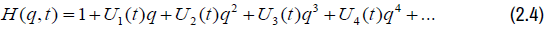
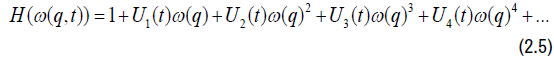
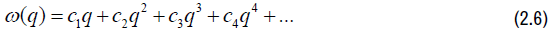
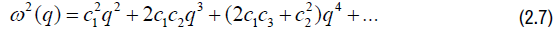
substituting (2.6),(2.7) and (2.8) in (2.4) we have
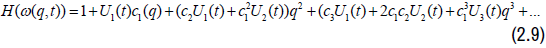
Equating (2.3) and (2.9) and comparing coefficients q, q2 and q3, applying equation (1.2) and Lemma 1.2 we have the result.
2.1 Fekete-Szego˙ Inequality
The Fekete-Szego˙ functional for the class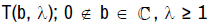 
is given here.
Theorem 2.3 If f (q) belongs to the class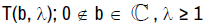 
then
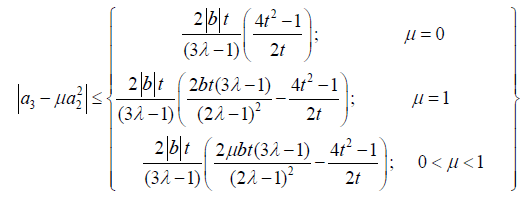
The classical geometric function theory was extended to functions of quaternionic variables in this work. A new class of function involving the Chebyshev polynomial of the second kind was defined. The coefficient bounds and the Fekete-Szego˙ functional for quaternionic functions were established using subordination principle.
(1.2) [