Research Article - (2020) Volume 14, Issue 1
Received: 18-Jan-2020
Published:
30-Jan-2020
, DOI: 10.37421/1736-4337.2020.14.296
Citation: Saeed Mortada, Simon Joseph and Ahmed Sufyan.“Universality of Affine Semigroups on Supercyclicity of the Sequence Operators.” J Generalized Lie Theory Appl 14 (2020). doi: 10.37421/glta.2020.14.296
Copyright: © 2020 Saeed M, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits
unrestricted use, distribution, and reproduction in any medium, provided the
original author and source are credited.
In this paper, show that for all supercyclic strongly continuous sequence of operators semigroup acting on a complex Fj -space, every 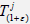 with ε > −1 is supercyclic. Furthermore, the set of supercyclic vectors of all
with ε > −1 is supercyclic. Furthermore, the set of supercyclic vectors of all 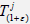 with ε > −1 is precisely the set of supercyclic vectors of the plenary semigroup.
with ε > −1 is precisely the set of supercyclic vectors of the plenary semigroup.
Hypercyclic semigroups • Hypercyclic operators • Supercyclic operators • Supercyclic semigroups
Unless stated otherwise, all vector spaces in this article are over the field
k, being either the field C of complex numbers or the field R of real numbers
and all topological spaces are assumed to be Hausdorff. As usual, Z+ is the
set of non-negative integers, N is the set of positive integers and R+ is the
set of non-negative real numbers. The symbol L(X) stands for the space of
a continuous linear sequence of operators on a topological vector space X,
while X in the space of continuous linear functionals on X. As usual, for Tj
∈L(X) the dual sequence of operators Tj : X'→ X' is defined by the formula 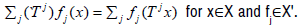 Recall that an affine map
on a Tj vector space X is a map of the shapes Tj x=uj + Sj x, where uj is fixed
vector in X and Sj : X→ X is linear. Clearly, Tj are continuous if and only if Sj
are continuous. The symbol Aj(X) stands for the space of continuous affine
maps on a topological vector space. Fj -space is a complete metrizable
topological vector space. Recall that a family
Recall that an affine map
on a Tj vector space X is a map of the shapes Tj x=uj + Sj x, where uj is fixed
vector in X and Sj : X→ X is linear. Clearly, Tj are continuous if and only if Sj
are continuous. The symbol Aj(X) stands for the space of continuous affine
maps on a topological vector space. Fj -space is a complete metrizable
topological vector space. Recall that a family 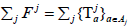 of
continuous maps from a topological space X to a topological space Y is
called universal if there is x∈X for which
of
continuous maps from a topological space X to a topological space Y is
called universal if there is x∈X for which 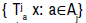 is dense in Y and
such an x is called a universal element for Fj. Use the symbol u(Fj) for the
set of universal elements for Fj. If X is a topological space and Tj : X→ X
is a continuous map, then say that x∈X is universal for Tj if x is universal
for the family
is dense in Y and
such an x is called a universal element for Fj. Use the symbol u(Fj) for the
set of universal elements for Fj. If X is a topological space and Tj : X→ X
is a continuous map, then say that x∈X is universal for Tj if x is universal
for the family 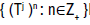 Denote the sets of universal elements for Tj by
Denote the sets of universal elements for Tj by 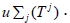 Series families
Series families 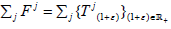 of continuous maps
from a topological space X to itself are called semigroups if
of continuous maps
from a topological space X to itself are called semigroups if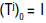 and
and 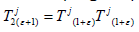 for every (1+ε)∈R+. Say that a semigroup
for every (1+ε)∈R+. Say that a semigroup 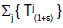 (1+ε)∈R+ is strongly continuous if (1+ε)→ Tj
(1+ε)x are continuous as a map from R+ to X for every x∈X and say that
(1+ε)∈R+ is strongly continuous if (1+ε)→ Tj
(1+ε)x are continuous as a map from R+ to X for every x∈X and say that 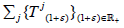 is jointly continuous if
is jointly continuous if 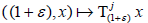 is continuous as a map from R+ × X to X. If X is
a topological vector space, semigroup
is continuous as a map from R+ × X to X. If X is
a topological vector space, semigroup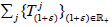 a linear semigroup if
a linear semigroup if 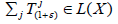 for every
for every 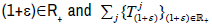 is called an
affine semigroup if
is called an
affine semigroup if 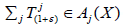 for every (1+ε)∈R+. Recall that Tj
∈L(X) is called hypercyclic if
for every (1+ε)∈R+. Recall that Tj
∈L(X) is called hypercyclic if 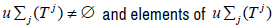 are called hypercyclic vectors. Universal linear semigroups
are called hypercyclic vectors. Universal linear semigroups 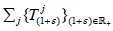 are called hypercyclic and its universal elements are called hypercyclic vectors for
are called hypercyclic and its universal elements are called hypercyclic vectors for 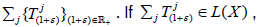 then universal elements of the family
then universal elements of the family 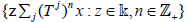 are called supercyclic vectors for Tj and Tj are called supercyclic if it has a supercyclic vector. Similarly, if
are called supercyclic vectors for Tj and Tj are called supercyclic if it has a supercyclic vector. Similarly, if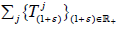 are linear semigroup, then a universal element of
the families
are linear semigroup, then a universal element of
the families 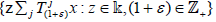 are called supercyclic vector
for
are called supercyclic vector
for 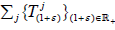 and the semigroup is called supercyclic if it has a
supercyclic vector.
and the semigroup is called supercyclic if it has a
supercyclic vector.
Hypercyclicity and supercyclicity have been studied during the last
decades [1]. The concern is the relation between the supercyclicity of a linear
semigroup and the supercyclicity of the individual members of the semigroup.
The hypercyclicity version of the question was treated by Conejero, Müller,
and Peris [2], who proved that for every strongly continuous hypercyclic
linear semigroups 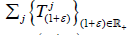 on an Fj-space, all
on an Fj-space, all 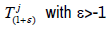 is hypercyclic and
is hypercyclic and 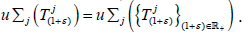 Virtually the same
proof works in the following much more general setting.
Virtually the same
proof works in the following much more general setting.
Theorem A
Let 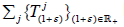 be a hypercyclic jointly continuous linear
semigroup on all topological vector space X. Then all
be a hypercyclic jointly continuous linear
semigroup on all topological vector space X. Then all 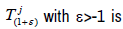 hypercyclic and
hypercyclic and 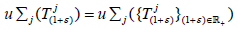
The stronger condition of joint continuity coincides with the strong
continuity in the case when X is an Fj -space due to a straightforward
application of the Banach–Steinhaus theorem. It is based on a homotopytype
argument and goes through without any changes for semigroups of
non-linear maps. Recall that a topological space X is called connected if it
has no subsets different from  and X, which are closed and open and it is
called simply connected if for any continuous map fj : T→X, there is a continuous
map Fj : T×[0,1]→X and x0∈Xsuch that Fj(z,0)=fj(z) and Fj(z,1)=x0for any z∈T.
Next, X is called locally path connected at χ∈X if for any neighborhood U of
χ, there is a neighborhood V of χ such that for any y∈V, there is a continuous
map fj :[0,1]→X satisfying fj (0)=x, fj (1)=y, and fj ([0,1]) ⊆ U. Space X is called
locally path-connected if it is locally path connected at every point. Just listing
the conditions to run smoothly, get the following result.
and X, which are closed and open and it is
called simply connected if for any continuous map fj : T→X, there is a continuous
map Fj : T×[0,1]→X and x0∈Xsuch that Fj(z,0)=fj(z) and Fj(z,1)=x0for any z∈T.
Next, X is called locally path connected at χ∈X if for any neighborhood U of
χ, there is a neighborhood V of χ such that for any y∈V, there is a continuous
map fj :[0,1]→X satisfying fj (0)=x, fj (1)=y, and fj ([0,1]) ⊆ U. Space X is called
locally path-connected if it is locally path connected at every point. Just listing
the conditions to run smoothly, get the following result.
Proposition 1.1
Let X be a topological space and 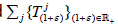 a jointly
continuous semigroup on X such that
a jointly
continuous semigroup on X such that
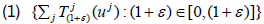 are nowhere dense in X for
every ε>-1 and uj ∈X ;
are nowhere dense in X for
every ε>-1 and uj ∈X ;
(2) for every ε>-1 and 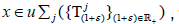 there is
there is 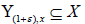 such that
such that 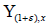 is connected, locally path-connected, simply connected
and
is connected, locally path-connected, simply connected
and
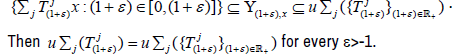
The natural question of whether the supercyclicity version of Theorem A holds in [3]. They have produced the following example.
Example B: Let X be a Banach space over R, 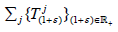 be a hypercyclic linear semigroup on X and
be a hypercyclic linear semigroup on X and 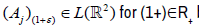 be the
linear sequence of operators with the matrices
be the
linear sequence of operators with the matrices 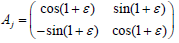 Then
Then 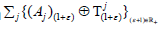 is supercyclic linear semigroup on
is supercyclic linear semigroup on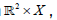 while
while 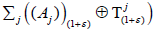 are non-supercyclics whenever
are non-supercyclics whenever 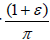 is rational.
is rational.
Example B shows that the natural supercyclicity version of Theorem A fails in the case k=R.
Proposition 1.2
Let X be a complex topological vector space and 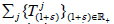 be a supercyclic jointly continuous linear semigroup on X such that
be a supercyclic jointly continuous linear semigroup on X such that 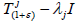 has a dense range for every ε>-1 and every λj∈C. Then each
has a dense range for every ε>-1 and every λj∈C. Then each 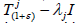 has a dense range for every ε>-1 and every λj∈C. Then each
has a dense range for every ε>-1 and every λj∈C. Then each 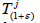 with ε>-1 is supercyclic. Furthermore, the set of supercyclic vectors for
with ε>-1 is supercyclic. Furthermore, the set of supercyclic vectors for 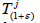 does not depend on the choice of ε>-1 and simultaneity with the set of
supercyclic vectors of the plenary semigroup.
does not depend on the choice of ε>-1 and simultaneity with the set of
supercyclic vectors of the plenary semigroup.
Whatever one can obtain the same result directly by considering the induced action on subsets of the projective space and applying Proposition 1.1. show that in the case k=C, the supercyclicity version of Theorem A holds without any additional assumptions.
Theorem 1.2
Let X be a complex topological vector space and 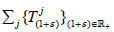 be a supercyclic jointly continuous linear semigroup on X. Then all
be a supercyclic jointly continuous linear semigroup on X. Then all 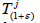 with ε>-1 is supercyclic and the set of supercyclic vectors of
with ε>-1 is supercyclic and the set of supercyclic vectors of 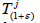 coincides with
the set of supercyclic vectors of
coincides with
the set of supercyclic vectors of 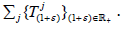
It turns out that any supercyclic jointly continuous linear semigroup on a complex topological vector X either satisfies conditions of Proposition Cor has a closed invariant hyperplane Y. Reduces the following generalization of Theorem A to affine semigroups [4].
Theorem 1.3
Let X be a topological vector space and 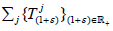 a
universal jointly continuous affine semigroup on X. Then all
a
universal jointly continuous affine semigroup on X. Then all 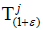 with ε>-1 is universal and
with ε>-1 is universal and 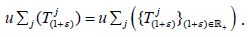
An analogue of the following result for supercyclic sequence of operators.
Proposition 2.1
Let X be a complex topological vector space and 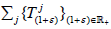 be a supercyclic strongly continuous linear semigroup on X. Then either
be a supercyclic strongly continuous linear semigroup on X. Then either 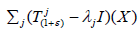 is dense in X for every ε>-1 and λj∈C or there is a
closed hyperplane Hin X such that
is dense in X for every ε>-1 and λj∈C or there is a
closed hyperplane Hin X such that 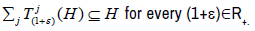
This section is devoted to the proof of Proposition 2.1. Recall that subsets Bj of vector space X are called balanced if λj x∈Bj for every x∈Bj
and λj∈k such that 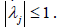
Proof: Assume that there is ε>-1 and λj∈k such that 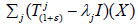 are not dense in X. By Lemma 2.5,
are not dense in X. By Lemma 2.5,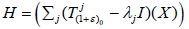 are closed
hyperplanes in X.
are closed
hyperplanes in X.
Lemma 2.2
Let K be a compact subset of an infinite dimensional topological vector
space and X such that 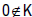 . Then
. Then 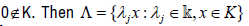 is a closed
nowhere dense subset of X.
is a closed
nowhere dense subset of X.
Proof: Closeness of Λ in X is a straightforward exercise. Assume that
Λ is not anywhere dense. Since Λ is closed, it's interior Lis non-empty.
Since Kis closed and 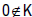 , find a non-empty balanced open set U such
that
, find a non-empty balanced open set U such
that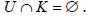 Obviously
Obviously 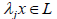 whensoever x ∈ L and
whensoever x ∈ L and 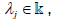
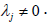 Since U is open and balanced property of Limplies that the open
set
Since U is open and balanced property of Limplies that the open
set 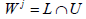 is non-empty. Taking into account the definition of Λ ,
inclusion
is non-empty. Taking into account the definition of Λ ,
inclusion 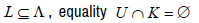 and the fact that Uis balanced,
every x ∈ Wj be written as x=λjy, where y∈k and
and the fact that Uis balanced,
every x ∈ Wj be written as x=λjy, where y∈k and 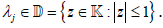 Since both Kand
Since both Kand 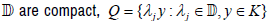 is a compact
subset of X. Since X ⊆ Q , Wj is a non-empty open set with compact
closure. Such a set exists [5] only if X is finite dimensional. This contradiction
completes the proof.
is a compact
subset of X. Since X ⊆ Q , Wj is a non-empty open set with compact
closure. Such a set exists [5] only if X is finite dimensional. This contradiction
completes the proof.
The following lemma is a particular case in [6].
Lemma 2.3
Let X be a complex topological vector space such that 2 ≤ dim X < ∞ . Then X supports no supercyclic strongly continuous linear semigroups.
Lemma 2.4
Let X be an infinite dimensional topological vector space 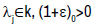 and
and 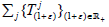 be a strongly continuous linear semigroup such that
be a strongly continuous linear semigroup such that 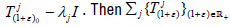 are not supercyclics.
are not supercyclics.
Proof: Let x∈ X \ {0} . It success to show that x is not a supercyclic
vector for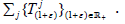
First, consider the case λj=0, it is ε>-1 such that 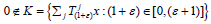 andK is a compact subset of X. By Lemma
2.2,
andK is a compact subset of X. By Lemma
2.2, 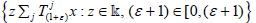 is nowhere dense in X. Take n∈N such that
is nowhere dense in X. Take n∈N such that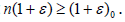 Since
Since 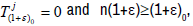 have
have  Notably, Y
is nowhere dense in X. Obviously,
Notably, Y
is nowhere dense in X. Obviously, 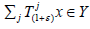 whenever ε>-1. Hence
whenever ε>-1. Hence 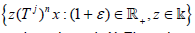 is contained in
is contained in 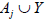 and therefore is
nowhere dense in X. Thus x is not a supercyclic vector for
and therefore is
nowhere dense in X. Thus x is not a supercyclic vector for 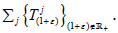
Suppose that λj≠0. Then 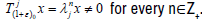 Hence each
of the compact sets
Hence each
of the compact sets 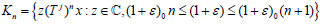 with n∈Z+ does not contain 0. The sets
with n∈Z+ does not contain 0. The sets 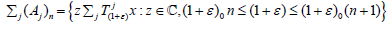 nowhere
dense in X. On the other hand, for every
nowhere
dense in X. On the other hand, for every 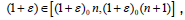
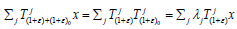 and therefore
and therefore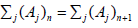 for each n ∈ Z
+
. Hence
for each n ∈ Z
+
. Hence 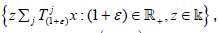 which is clearly
the union of
which is clearly
the union of 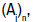 coincides with
coincides with 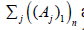 therefore is nowhere
dense. Thus x is not a supercyclic vector for
therefore is nowhere
dense. Thus x is not a supercyclic vector for 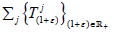
Lemma 2.5
Let X be a complex topological vector space and  bea supercyclic strongly continuous linear semigroup on X. Let also (ε+1)0 >0 and λj∈C Then space
bea supercyclic strongly continuous linear semigroup on X. Let also (ε+1)0 >0 and λj∈C Then space 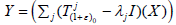 coincides with X
or is a closed hyperplane in X.
coincides with X
or is a closed hyperplane in X.
Proof: Using the semigroup property. Factoring Y out, arrive in a
supercyclic strongly continuous linear semigroup 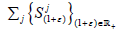 acting on X/Y, where
acting on X/Y, where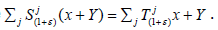 Clearly,
Clearly,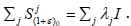 If X/Y is infinite dimensional, arrive at a contradiction
with Lemma 2.4. If X/Y is finite dimensional and dim X / Y ≥ 2 , we obtain
a contradiction with Lemma 2.3. Thus dim X/Y≤ 1, as required.
If X/Y is infinite dimensional, arrive at a contradiction
with Lemma 2.4. If X/Y is finite dimensional and dim X / Y ≥ 2 , we obtain
a contradiction with Lemma 2.3. Thus dim X/Y≤ 1, as required.
Lemma 2.6
Let X be a complex topological vector space and 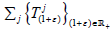 be a strongly continuous linear semigroup on X. Assume also that there
is a closed hyperplane Hin X such that
be a strongly continuous linear semigroup on X. Assume also that there
is a closed hyperplane Hin X such that 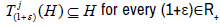 and let fj∈X’ be such that H=ker fj. Then there exists w ∈Csuch that
and let fj∈X’ be such that H=ker fj. Then there exists w ∈Csuch that 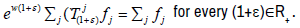
Proof: Since H=ker fj is invariant for every 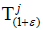 , there is a unique function
, there is a unique function 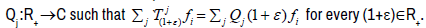 Pick uj
∈X such that
Pick uj
∈X such that 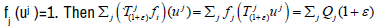 for every
for every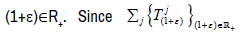 strongly continuous,
Qj is continuous. The semigroup property for
strongly continuous,
Qj is continuous. The semigroup property for 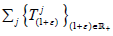 implies the semigroup property for the dual sequence of operators:
implies the semigroup property for the dual sequence of operators: 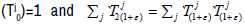 for every (1+ε)∈R+. Together
with equality
for every (1+ε)∈R+. Together
with equality 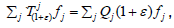 it implies that Qj(0)=1 and
it implies that Qj(0)=1 and 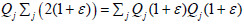 for every (1+ε)∈R+. The latter and
the continuity of Qj means that there is w∈C such that
for every (1+ε)∈R+. The latter and
the continuity of Qj means that there is w∈C such that 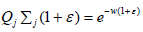 for each (1+ε)∈R+. Thus
for each (1+ε)∈R+. Thus 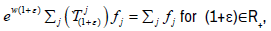 as required.
as required.
Start with the following general lemma.
Lemma 3.1
Let X=1 be a topological vector space, uj∈X, \ {0} fj∈ X′ ,f(uj)=1 and
H=ker fj. Assume also that 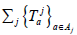 isa family of a continuous linear
sequence of operators on X such that
isa family of a continuous linear
sequence of operators on X such that 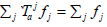 for each a∈Aj.
Then the families
for each a∈Aj.
Then the families 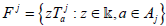 are universals if and only if
the families
are universals if and only if
the families 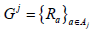 of affine maps
of affine maps 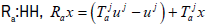 are universals on H. Moreover, x∈X is universal for Fj if and only if x = λj (uj+w), where λj ∈k\{0} and w is universal for Gj. Next, if Aj = Z+ and
are universals on H. Moreover, x∈X is universal for Fj if and only if x = λj (uj+w), where λj ∈k\{0} and w is universal for Gj. Next, if Aj = Z+ and 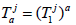 for every a∈Z+, then
for every a∈Z+, then 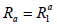 for every a∈Z+. Finally, if Aj
for every a∈Z+. Finally, if Aj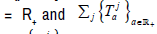 is strongly continuous linear semigroup, then
is strongly continuous linear semigroup, then  is strongly continuous affine semigroup.
is strongly continuous affine semigroup.
Proof: Since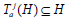 for every a, vectors from H cannot be
universal for Fj. Clearly, they also do not have the form
for every a, vectors from H cannot be
universal for Fj. Clearly, they also do not have the form 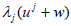 with
with 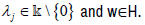
Let 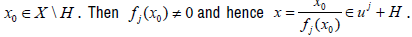 Since
Since 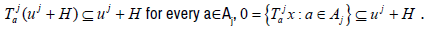 It is straightforward to see that x0 is universal for Fj if and only if 0 is dense in uj +H. That is, x0 is universal for Fj if and only if x is universal for the families
It is straightforward to see that x0 is universal for Fj if and only if 0 is dense in uj +H. That is, x0 is universal for Fj if and only if x is universal for the families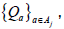 where each
where each 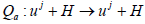 is the restriction of
is the restriction of 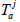 to
the invariant subset uj +H. Clearly, the translation map
to
the invariant subset uj +H. Clearly, the translation map 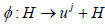
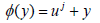 is a homeomorphism and
is a homeomorphism and 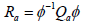 for every a∈Aj. It
follows that x0 is universal for Fj if and only if
for every a∈Aj. It
follows that x0 is universal for Fj if and only if 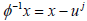 is universal for Gj. Denoting w=x-uj, if and only if
is universal for Gj. Denoting w=x-uj, if and only if 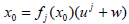 with
with 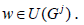
Since Qa are the restrictions of Tja to the invariant subset uj +H and Ra
are similar to Qa in the same manner independent on a, {Ra} inherits all the
semigroup or continuity properties from 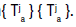 The proof is complete.
The proof is complete.
Lemma 3.2
Let X be a topological vector space, 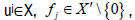 and H=ker
fj. Then
and H=ker
fj. Then 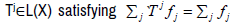 is supercyclic if and only if
the map
is supercyclic if and only if
the map 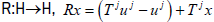 is universal. Moreover, x∈X is
a supercyclic vector for Tj if and only if x=λj (uj+w), where λj∈k \{0} and
w∈U(R).
is universal. Moreover, x∈X is
a supercyclic vector for Tj if and only if x=λj (uj+w), where λj∈k \{0} and
w∈U(R).
Lemma 3.3
Let X be a topological vector space, 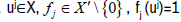 H=ker fj. Then a strongly continuous linear semigroup
H=ker fj. Then a strongly continuous linear semigroup 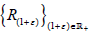 on X
satisfying
on X
satisfying 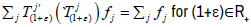 is supercyclic if and only
if the strongly continuous affine semigroup
is supercyclic if and only
if the strongly continuous affine semigroup 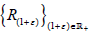 on H defined
by
on H defined
by 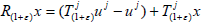 universals. Furthermore, x∈X is
a supercyclic vector for
universals. Furthermore, x∈X is
a supercyclic vector for 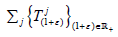 if and only if x=λj (uj+w), where
if and only if x=λj (uj+w), where 
The proof of the following lemma is a routine verification.
Lemma 4.1
Let X be a topological vector space, 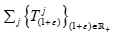 a collection
of continuous affine maps on
a collection
of continuous affine maps on 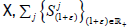 be a collection of the
continuous linear sequence of operators on X and (1+ε)→w(1+ε) be a map
from R+ to X such that
be a collection of the
continuous linear sequence of operators on X and (1+ε)→w(1+ε) be a map
from R+ to X such that 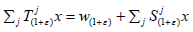 for every (1+ε)∈R+ and x∈X. Then
for every (1+ε)∈R+ and x∈X. Then 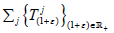 are affines semigroup if and only if
are affines semigroup if and only if 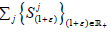 are linear semigroups,
are linear semigroups,
W0 =0 and 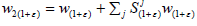 for every (1+ε)∈R+ . (1)
for every (1+ε)∈R+ . (1)
Furthermore, the semigroup 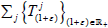 is strongly continuous
if and only if
is strongly continuous
if and only if 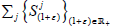 is strongly continuous and the map
is strongly continuous and the map 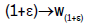 is continuous. Finally, the semigroup
is continuous. Finally, the semigroup 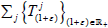 is
jointly continuous if and only if
is
jointly continuous if and only if 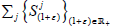 is jointly continuous and the map (1+ε)→w(1+ε) is continuous.
is jointly continuous and the map (1+ε)→w(1+ε) is continuous.
Lemma 4.2
Let X be a topological vector space and 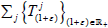 be a universal strongly continuous affine semigroup on X. Then
be a universal strongly continuous affine semigroup on X. Then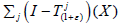 is dense in X for every ε>-1.
is dense in X for every ε>-1.
Proof: Suppose the contrary. Then there is ε>-1 such that Y0 ≠ X, where 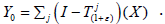 Let Y be a translation of Y0, containing
Let Y be a translation of Y0, containing 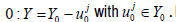 Factoring out the closed linear subspace Y, arrive
in the universal strongly continuous affine semigroup
Factoring out the closed linear subspace Y, arrive
in the universal strongly continuous affine semigroup 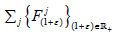 on X/Y, where
on X/Y, where 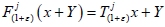 for every (1+ε)∈R+ and
x∈X. By definition of Y, the linear part of
for every (1+ε)∈R+ and
x∈X. By definition of Y, the linear part of 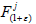 is I. Let β+ε∈X/Y be a
universal vector for
is I. Let β+ε∈X/Y be a
universal vector for 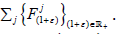 By Lemma 4.1, there is a strongly
continuous linear semigroup
By Lemma 4.1, there is a strongly
continuous linear semigroup 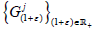 on X/Y and a continuous map
on X/Y and a continuous map 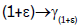 from R+ to X/Y such that
from R+ to X/Y such that 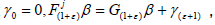 and
and 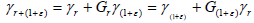 for every β∈X/Y and r, (1+ε)∈R+,
obtain that
for every β∈X/Y and r, (1+ε)∈R+,
obtain that 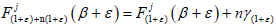 for every n∈Z+
and (ε+1)∈R+. It follows that
for every n∈Z+
and (ε+1)∈R+. It follows that
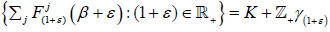
where
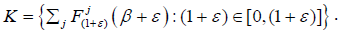
Since (β+ε) is universal for 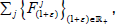 hence,
hence, 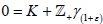 is dense in X/Y. Since 0 is closed as a sum of a compact set and a closed
set,0=X/Y. On the other hand, 0 it does not contain
is dense in X/Y. Since 0 is closed as a sum of a compact set and a closed
set,0=X/Y. On the other hand, 0 it does not contain 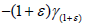 any
sufficiently large >-1. This contradiction completes the proof.
any
sufficiently large >-1. This contradiction completes the proof.
Lemma 4.3
Let X be a topological vector space, x∈X, ε>-1 and 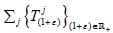 be a universal affine semigroup on X. Assume also that
be a universal affine semigroup on X. Assume also that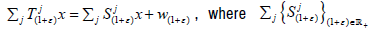 continuous linear semigroup on X and
continuous linear semigroup on X and 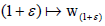 is a continuous
map from R+ to X. Then
is a continuous
map from R+ to X. Then 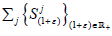 is hypercyclic. Furthermore,
is hypercyclic. Furthermore, 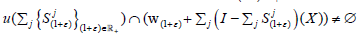 for every ε > -1.
for every ε > -1.
Proof: Let 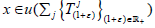 and fixε ε > -1. By Lemma
4.2,
and fixε ε > -1. By Lemma
4.2, 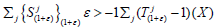 are dense in X. Hence
are dense in X. Hence 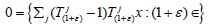 are dense in X. Using the semigroup property of
are dense in X. Using the semigroup property of 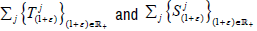 together with (1), get
together with (1), get
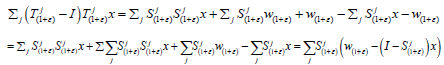 for every
for every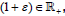 then, 0 is exactly the St-orbit of
then, 0 is exactly the St-orbit of 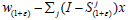 . Since o is dense in
. Since o is dense in 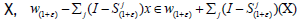 is hypercyclic vector for
is hypercyclic vector for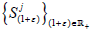 and therefore
and therefore 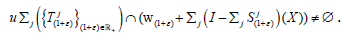
Lemma 4.4
Let X be a topological vector space and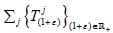 be an affine
semigroup on X. Then for every
be an affine
semigroup on X. Then for every 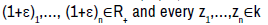 satisfying
satisfying 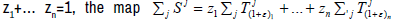 commutes with every
commutes with every 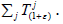
Proof: To verify that for every affine map Aj : X→X and every x1,….,xn∈X,
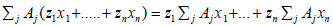 provided zj∈k
and z1+… zn=1.
provided zj∈k
and z1+… zn=1.
Let (1+ε)∈R+. Therefore,
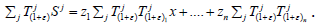
Since 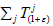 commute with each other, get
commute with each other, get
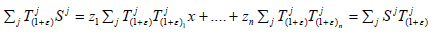
Lemma 4.5
Let X be a topological vector space, 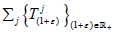 be universals
strongly continuous affine semigroup on X and
be universals
strongly continuous affine semigroup on X and 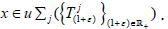 Then
Then 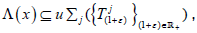 where
where
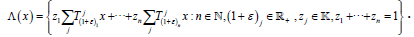 (2)
(2)
Proof: Let 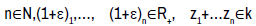 and z1+……
zn=1. Have to show that
and z1+……
zn=1. Have to show that 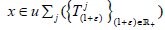 where
where 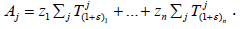 A commute with all
A commute with all 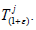 Since
Since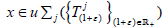 it suffices to verify that Aj(X) are
dense in X. By Lemma 4.1, write
it suffices to verify that Aj(X) are
dense in X. By Lemma 4.1, write 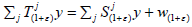 for every y∈X, where
for every y∈X, where 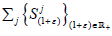 is strongly continuous
linear semigroup on X and (1+ε)→w(1+ε) is a continuous map from
R+ to X. By Lemma 4.3,
is strongly continuous
linear semigroup on X and (1+ε)→w(1+ε) is a continuous map from
R+ to X. By Lemma 4.3, 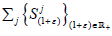 are hypercyclics. Thus
are hypercyclics. Thus 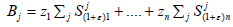 has dense range. Since Aj(X) is
translation, Bj(X),Aj(X) is also dense in X, which completes the proof.
has dense range. Since Aj(X) is
translation, Bj(X),Aj(X) is also dense in X, which completes the proof.
Let X be a topological vector space and 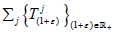 be a
universal jointly continuous affine semigroup on X. By Theorem A, there is
a hypercyclic continuous linear operator on X. Since no such thing exists on
a finite-dimensional topological vector space [7], X is infinite-dimensional.
Since any compact subspace of an infinite-dimensional topological vector
space is nowhere dense [4], condition (1) of Proposition 1.1 is satisfied. Let
be a
universal jointly continuous affine semigroup on X. By Theorem A, there is
a hypercyclic continuous linear operator on X. Since no such thing exists on
a finite-dimensional topological vector space [7], X is infinite-dimensional.
Since any compact subspace of an infinite-dimensional topological vector
space is nowhere dense [4], condition (1) of Proposition 1.1 is satisfied. Let 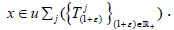 By Lemma 4.5, the set Λ(x) defined in (4.2)
consists entirely of universal vectors for
By Lemma 4.5, the set Λ(x) defined in (4.2)
consists entirely of universal vectors for 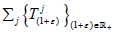 . Obviously,
. Obviously, 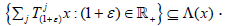 By its definition, Λ(x) is an affine
subspace of X. Λ(x) satisfies all requirements for the set
By its definition, Λ(x) is an affine
subspace of X. Λ(x) satisfies all requirements for the set 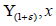 (for
every ε > -1) from condition (2) in Proposition 1.1. By Proposition 1.1,
(for
every ε > -1) from condition (2) in Proposition 1.1. By Proposition 1.1, 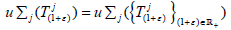 for every ε > -1, as required.
for every ε > -1, as required.
Let X be a complex topological vector space and 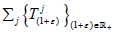 be a supercyclic jointly continuous linear semigroup on X in [8]. To
prove that all
be a supercyclic jointly continuous linear semigroup on X in [8]. To
prove that all 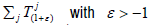 supercyclic and the sets of
supercyclic vectors of
supercyclic and the sets of
supercyclic vectors of 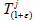 simultaneity with the set of supercyclic
vectors of
simultaneity with the set of supercyclic
vectors of 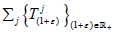 . If
. If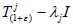 has a dense range for every
ε > -1 and every λj∈C, then Proposition C provides the required result.
Else, by Proposition 2.1, there is a closed hyperplane H in X invariant
for all
has a dense range for every
ε > -1 and every λj∈C, then Proposition C provides the required result.
Else, by Proposition 2.1, there is a closed hyperplane H in X invariant
for all 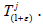 By Lemma 2.6, there is fj∈X and (β+ε)∈C such that H=kerfj and
By Lemma 2.6, there is fj∈X and (β+ε)∈C such that H=kerfj and 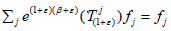 for every (1+ε)∈R+. Obviously
for every (1+ε)∈R+. Obviously 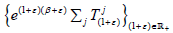 is a jointly continuous supercyclic linear
semigroup on X with the same sets Sj of supercyclic vectors as the original semigroup
is a jointly continuous supercyclic linear
semigroup on X with the same sets Sj of supercyclic vectors as the original semigroup 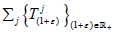 . Fix uj∈X satisfying fj(uj)=1. Now
fix ε>-1 and vj ∈Sj. Have to show that vj is supercyclic for
. Fix uj∈X satisfying fj(uj)=1. Now
fix ε>-1 and vj ∈Sj. Have to show that vj is supercyclic for 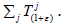 By Lemma 3.3, applied to the semigroup
By Lemma 3.3, applied to the semigroup 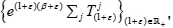 write
write 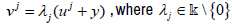 and y is a universal vector for the jointly continuous affine semigroup
and y is a universal vector for the jointly continuous affine semigroup 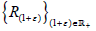 on H defined by the formula
on H defined by the formula 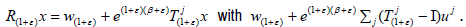 By Theorem 1.3, y is universal for R(1+ε). By Lemma 3.2,
By Theorem 1.3, y is universal for R(1+ε). By Lemma 3.2, 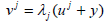 is a supercyclic vector for
is a supercyclic vector for 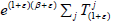 and hence vj is a supercyclic vector for
and hence vj is a supercyclic vector for 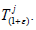 The proof is complete.
The proof is complete.
By Lemma 4.3, the universality of a strongly continuous affine semigroup implies hypercyclicity of the underlying linear semigroup. The following example shows that the converse is not true [4].
Example 6.1
Consider the backward weighted shift Tj∈L(l2) with the weight sequence 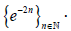 That is,
That is, 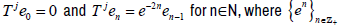 is the standard basis of l2. Then the jointly continuous linear semigroups
is the standard basis of l2. Then the jointly continuous linear semigroups 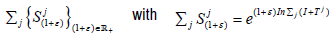 are hypercyclics. Furthermore, there exists a continuous map
are hypercyclics. Furthermore, there exists a continuous map 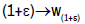 from R+ to l2
such that
from R+ to l2
such that 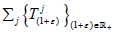 is jointly continuous non-universal affine
semigroup, where
is jointly continuous non-universal affine
semigroup, where 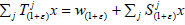 for x∈l2.
for x∈l2.
Proof: Since Tj being compacts weighted backward shift, is
quasinilpotent, the sequence of operators ln 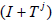 is well defined
and bounded and
is well defined
and bounded and 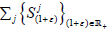 is a jointly continuous linear
semigroup. Moreover,
is a jointly continuous linear
semigroup. Moreover, 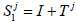 are hypercyclics [9] as a sum of the
identical sequence of operators and a backward weighted shift. Hence
are hypercyclics [9] as a sum of the
identical sequence of operators and a backward weighted shift. Hence 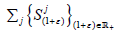 are hypercyclics.
are hypercyclics.
Let 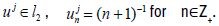 For each (1+ε)∈R+, let
For each (1+ε)∈R+, let 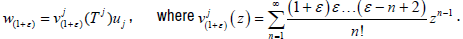 Since Tj are quasinil potents,
Since Tj are quasinil potents, 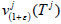 are well defined bounded linear
sequence of operators and the map
are well defined bounded linear
sequence of operators and the map 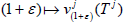 are a sequence
of operators-norm continuous. Hence (1+ε)→w(1+ε) is continuous as a map from R+ to l2, to verify that w0=0, w1=uj and
are a sequence
of operators-norm continuous. Hence (1+ε)→w(1+ε) is continuous as a map from R+ to l2, to verify that w0=0, w1=uj and 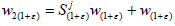 for every ε>-1. By Lemma 4.1,
for every ε>-1. By Lemma 4.1, 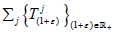 is a jointly continuous
affine semigroup, where
is a jointly continuous
affine semigroup, where 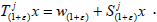 It remains to show that
It remains to show that 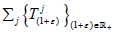 is non-universal. Assume the contrary. Since w1=uj and
is non-universal. Assume the contrary. Since w1=uj and 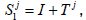 Lemma 4.3 implies that the coset
Lemma 4.3 implies that the coset 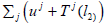 must
contain a hypercyclic vector for I+Tj. This, however, is not the case as
shown in [10].
must
contain a hypercyclic vector for I+Tj. This, however, is not the case as
shown in [10].
Remark 6.2
Let X be a topological vector space and 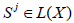 be hypercyclic.
If
be hypercyclic.
If 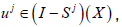 then the affine map
then the affine map 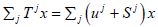 is universal. Actually, let w∈X be such that
is universal. Actually, let w∈X be such that 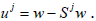 It is easy to show
that
It is easy to show
that 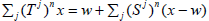 for every x∈X and n∈N. Thus x is universal for Tj if and only if x-w is universal for Sj.
for every x∈X and n∈N. Thus x is universal for Tj if and only if x-w is universal for Sj.
If additionally X is separable metrizable and Baire, then a standard
Baire category type argument shows that the set of uj∈Xfor which the affine
map 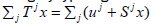 is universal is a dense Gδ -subset of X.
is universal is a dense Gδ -subset of X.
Example 6.1 shows that this set can differ from X.
Recall that a locally convex topological vector space X is called barrelled
if every closed convex balanced subset Bj of X satisfying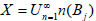 contain a neighborhood of 0. The joint continuity of a linear semigroup
follows from the strong continuity if the underlying space X is an Fj-space.
The same is true for wider classes of topological vector spaces. For the
case, it is sufficient X to be a Baire topological vector space or a barreled
locally convex topological vector space. Thus the following observation
holds true.
contain a neighborhood of 0. The joint continuity of a linear semigroup
follows from the strong continuity if the underlying space X is an Fj-space.
The same is true for wider classes of topological vector spaces. For the
case, it is sufficient X to be a Baire topological vector space or a barreled
locally convex topological vector space. Thus the following observation
holds true.
Remark 6.3
The joint continuity condition in Theorems A, 1.2 and 1.3 can be replaced by the strong continuity, provided X is Baire or X is locally convex and barrelled.
For general topological vector spaces however strong continuity of a
linear semigroup does not imply joint continuity. Furthermore, the following
example shows that Theorem A fails in general if the joint continuity condition
is replaced by strong continuity. Recall that the Fréchet space 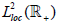 consists of the scalar-valued functions R+, square-integrable on [0,(1+ε)] for
each ε>-1. Its dual space can be naturally interpreted as the space
consists of the scalar-valued functions R+, square-integrable on [0,(1+ε)] for
each ε>-1. Its dual space can be naturally interpreted as the space 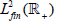 duality between
duality between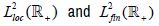 is provided by the natural dual
pairing
is provided by the natural dual
pairing 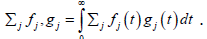 Clearly, the linear semigroup
Clearly, the linear semigroup 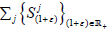 of backward shifts
of backward shifts 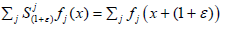 is strongly continuous and therefore jointly continuous on the Fréchet space
is strongly continuous and therefore jointly continuous on the Fréchet space 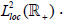 It follows that the same semigroup is strongly continuous on
It follows that the same semigroup is strongly continuous on  endowed with the weak topology.
endowed with the weak topology.
Example 6.4
Let 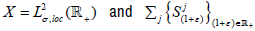 be the above strongly continuous semigroup on X. Then there are fj∈X hypercyclics for
be the above strongly continuous semigroup on X. Then there are fj∈X hypercyclics for 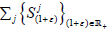 such that f
such that f
are not-hypercyclics for Sj1.
Proof: Let H be the hyperplane in L2 [0,1] consisting of the functions
with zero Lebesgue integral. Fix norm-dense countable subsets Aj of H. One
can easily construct 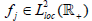 such that for every n∈N, the function
such that for every n∈N, the function 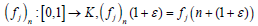 belongs to A
belongs to A
; for every n∈N and 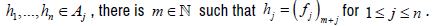
For 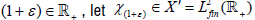 be the indicator function of the interval
be the indicator function of the interval 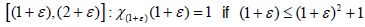 and
and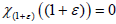 otherwise. By (a),
otherwise. By (a), 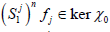 every
n∈N and therefore fj are not hypercyclics vector for Sj1.
every
n∈N and therefore fj are not hypercyclics vector for Sj1.
It remains to show that fj are hypercyclics vector for 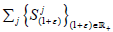 acting on X. Using (a) and (b), we see that the Fréchet space topology closure of the orbits
acting on X. Using (a) and (b), we see that the Fréchet space topology closure of the orbits 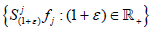 is exactly the sets
is exactly the sets
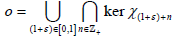
In order to show that fj are hypercyclics for 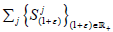 acting on
X, it suffices to verify that 0 is dense in
acting on
X, it suffices to verify that 0 is dense in 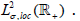 Assume the contrary.
Then there is a weakly open set
Assume the contrary.
Then there is a weakly open set 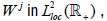 which does not intersect
0. That is, there are linearly independent
which does not intersect
0. That is, there are linearly independent 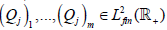 and
and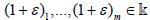 such that
such that
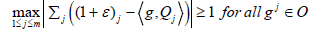
Let k∈N be such that all Qj vanishes on [k,∞) . Pick any 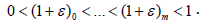 Note that for every 1≤ j ≤ m,
the restrictions of the functionals Qj to
Note that for every 1≤ j ≤ m,
the restrictions of the functionals Qj to 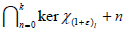 are
not linearly independent, see [11]. Actually, otherwise can find
are
not linearly independent, see [11]. Actually, otherwise can find 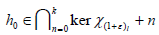 such that
such that 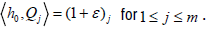 It is
easy to see that it is
It is
easy to see that it is 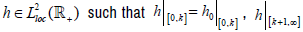 and
and  and
and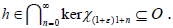 arrived at a contradiction.
arrived at a contradiction.
The fact that Qj is not linearly independents on 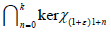 implies that there is a non-zero
implies that there is a non-zero 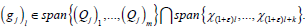 Since
Since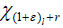 they are all linearly independent,
they are all linearly independent, 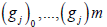 they are m +1 linearly independent vectors in the m dimensional space span
they are m +1 linearly independent vectors in the m dimensional space span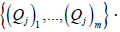 completes the proof.
completes the proof.
The authors declare that there is no conflict of interest.
The author thanks Colleagues for numerous helpful suggestions, and the referee for carefully checking the manuscript.