Site Selection Study for Refinery Using GIS and Logit, Probit Models

Saeed Sadrzadeh Moghadam^1*, Shahram Golestani² and Safieh Azimzadeh^1
*Correspondence: Saeed Sadrzadeh Moghadam, Department of Economics, University of Shahid Bahonar, Kerman, Iran, Email:

Keywords

Site selection • Boolean model • Geographical Information system • Oil refinery production • Logit • Probit model

Introduction

Locating an industry has economically an important role in both initial investments in industries establishment and the finished cost of products or services at exploitation time. Establishing one or more industrial units in optimal locations improves the distribution of materials and services among different shareholders in the supply chain and hence places the industry in a desired and sustainable state. Decisions related to selection and the locating characteristics of a center can have a great effect on the ability to acquire and maintain competitive advantage.

Analyzing the rapid ROI (Return of investment) firms reveals that more than 50 percent of them are bankrupted in the first year and 30 percent are bankrupted after two years and switch to another business. Despite considering all aspects of appropriate service providing at initiation but neglecting location considerations leads to the producer’s disability to fulfill the desired profit and achieve its targets.

In this study, concerning the importance of locating the industries and the positive effects of selecting an optimized location on profitability and survival of industries in one hand and also Iran's available potentials in the oil industry (the second producer of crude oil in OPEC and the fourth producer of crude oil in the world)in another hand and finally, problems in oil industry distribution area such as the excess concentration of the existing refinance in the western and southern regions of the country and existence of more oil-based products demand than the production capacity, optimal locating a new crude oil refinery is investigated.

Methodology

JL Redondo, J Fernandez, I Garc´ıa and PM Ortigosa introduced a robust and efficient global optimization algorithm for planar competitive location problems. They have presented four parallelizations of UEGO (Universal Evolutionary Global Optimizer) Carried out to compare the performance of the parallel algorithms. The results show that one of the parallelizations always gives the best objective function value and has an almost linear speedup for up to 16 processing elements for large instances. A company wants to expand its presence in a given geographical region by opening a new facility. The goal pursued by the chain is to increase its profit. The location and the quality of the new facility are the variables of the problem.

Unjie HONG and Anthony TH CHIN modelling the location choices of foreign investments in the Chinese logistics industry. They attempt to identify the location determinants of foreign investment in the Chinese logistics industry. Based on a theoretical model, a nested logit model is introduced and estimated using data on 1775 foreign logistics establishments. We find that a large market size attracts foreign investment, but high labour costs act as a deterrent. Good transportation infrastructure and high labour quality are positive factors. Capital cities attract more logistics investment, but there is no evidence that special economic zones and open coastal cities have significant advantages in attracting logistics investment.

Kala Seetharam Sridhar, Guanghua WAN contributes to the industrial location literature by examining why industry locates or refrains from locating in large, medium and small cities of India, China and Brazil using firm-level data from the World Bank. Results from ordered logistic regressions indicate that capital cities are not attractive for firms to locate when they are large. In India and China, labor-intensive firms do not locate in large cities. Proximity to inputs has a positive impact on the firm location in China. While the availability of inputs has a positive impact on the firm location in India, the availability of raw materials harms the firm location in Brazil. Firms established in the post-reform period in India tend to locate in large cities; in China, these firms avoid medium and large cities. The implications for urban governance in these countries are discussed.

Sridhar assesses the qualitative impacts of firm location on local economies and finds that firms have favorable impacts on the local labor markets where they have located. Sridhar studies the employment impact of growth centers in India. When they locate in a city, firms make an investment; create jobs, income and output. For these reasons, firm locational choices in cities (which we study in this paper) affect the ability of cities to become engines of macroeconomic growth. It is evident that cities are engines of macroeconomic growth in these countries as of 2000, 81% of Brazil was urbanized, with 90% of its GDP being generated in cities.1 The urban sector in China accounts for 70% of the nation's GDP and the corresponding contribution in India is about 50%, which is expected to reach 65% by 2011.

Yang Y, et al. [1] study to investigate potential factors contributing to the hotel location choice by an ordered logit model incorporating both hotel and location characteristics. The results suggest that star rating, years after opening, service diversification, ownership, agglomeration effect, public service infrastructure, road accessibility, subway accessibility and accessibility to tourism sites are important determinants. By examining location models for different periods, different star rating levels and different ownership, they show that downscale hotels tend not to actively seek the benefits of agglomeration effects while upscale ones are more sensitive to accessibility. Finally, agglomeration effects are further investigated by looking into agglomeration heterogeneity, agglomeration scope, scale-related and ownership-related agglomeration and agglomeration zoning.

Küçükaydin H, et al. [2] employs Huff’s gravity-based rule in modeling the behavior of the customers where the fraction of customers at a demand point that visits a certain facility is proportional to the facility attractiveness and inversely proportional to the distance between the facility site and demand point. They formulate a bilevel mixed-integer nonlinear programming model where the firm entering the market is the leader and the competitor is the follower. In order to find the optimal solution of this model, they convert it into an equivalent one-level mixed-integer nonlinear program so that it can be solved by global optimization methods. Apart from reporting computational results obtained on a set of randomly generated instances, we also compute the benefit the leader firm derives from anticipating the competitor’s reaction of adjusting the attractiveness levels of its facilities. The results on the test instances indicate that the benefit is 58.33% on average.

Miller TC, et al. [3] focus on the equilibrium facility location modeling. The developed mathematical models therein consider a firm that has to simultaneously decide on the production and distribution of a single, homogeneous product such that there exists equilibrium in the market represented as a network. The entering firm, usually called a Stackelberg or leader firm, anticipates the reaction of the follower firms that have existing facilities in the market. These followers are assumed to be Cournot firms trying to achieve a Nash equilibrium by making changes in their production and distribution levels as a reaction to the leader firm. However, these firms operate under the Cournot assumption that the others do not change their production and distribution levels. The novelty here is that the Cournot–Nash equilibrium of the followers is represented as a variational inequality formulation. In order to compute the Cournot–Nash and Stackelberg–Cournot–Nash equilibria, many heuristic algorithms employing sensitivity analysis are suggested.

Bhadury J, et al. [4] considers a discrete CFL with two competitors. Each competitor sells the same product to customers which are aggregated at discrete points in space called markets. One of the competitors becomes the leader and the other takes the role of the follower. Both of the decision-makers want to determine both the locations of a fixed number of new facilities to be established from a set of potential sites and the price of the product at each market. It is assumed that the product can be sold at different prices at different markets (i.e., discriminatory pricing) where the price at a market depends on the distance from the facility serving the market. Customers prefer to make the purchase from the competitor offering the lowest price. Fischer (2002) formulates two bi-level models: a mixed-integer nonlinear bilevel model in which both players fix their locations and prices once and for all and a linear bilevel model with binary variables where price adjustment is possible. A heuristic solution procedure is developed to solve the linear bilevel model, but no computational results are provided.

Bhadury J, et al. [4] suggests a centroid model in the continuous space, where the follower locates extra facilities as a reaction to the leader’s action. Drezner A [5] introduces two problems. In the first one, a new facility is located to attract most of the buying power from the demand points when there is already an existing facility in the market, whereas the second problem involves again the location of a new facility with the same goal, but this time by taking into account the possibility that the competitor opens a facility in the future. Plastria F and Vanhaverbeke L [6] consider the maximal covering model and incorporate into this model the information that a competitor will enter the market with a new facility in the future. The objective of the leader is to locate facilities under a budget constraint to maximize the market share after the competitor’s entry. The authors formulate three models corresponding to three strategies: worst-case analysis (maximin strategy), the minimum regret strategy and the Stackelberg strategy which corresponds to taking into account the objective function of the competitor. Serra and ReVelle develop a model where both the leader and follower locate an equal number of facilities that are visited by customers only if they are the closest ones. In this model, the objective of the leader is to minimize the market share of the follower and two heuristic algorithms are proposed for its sm most of the studies in this class consider the competition of the firms for a single homogeneous product as a two-stage game, where in the first stage both firms simultaneously decide where to locate the facilities. As soon as these decisions are made, they become known to both firms and they continue with the second stage of the game by simultaneously deciding either on the production quantities to supply the markets or on their products’ prices. Markets are usually located on the vertices of a network and firms aim at maximizing their profits. Based on some conditions, the uniqueness and existence properties of a Nash equilibrium for quantities or prices are shown. By means of additional conditions, the equilibrium locations are proved to be the vertices of the network. Among the papers including this type of analysis, we can mention Labbé M and Hakimi SL [7], Lederer PJ and Hurter Jr AP [8] and Lederer PJ and Thisse JF [9]. Sarkar J, et al. [10] extends the work of Labbé M and Hakimi SL [7] for multiple firms and nonlinear price functions.

Wendell RE and McKelvey RD [11] consider only the locational game for two competing firms on a graph and seek for a locational equilibrium such that a firm can capture at least 50% of the customers regardless where its competitor is located. By making use of the voting theory, necessary and sufficient conditions for locational equilibrium are developed. Rhim H, et al. [12] extend the spatial competition on a discrete space to an oligopolistic three-stage game, where in the first stage facility locations, in the second stage facility capacities and in the third stage quantities to be produced are decided. Pérez MDG, et al. [13] investigate only the second stage of the game, where the competition between multiple firms takes place only in terms of prices.

The CFL models in which players act sequentially can be further divided into two groups. In the first group, the entrant firm aims to open new facilities in a market where there are one or more competitors having existing facilities. However, they do not react to the entrant firm. Such models can be considered as a sequential-entry CFL model since the competitors have moved first and entered the market before the new entrant firm. The latter decides on its strategy about opening new facilities being aware of the location and attractiveness levels of the existing facilities [14-23].

Model

In this research, we divided the variables affecting the oil refinery optimal locating into two main criteria. The first criteria include geographical factors which are analyzed in geographical information system (earth ground slope, altitude, distance from cities, communicating roads, faults, rivers and underground water resources and lakes) and the second criteria includes factors that can be quantitatively inserted into logit model (such as region’s land price and labor cost).

At the first stage, required primary maps for each factor are prepared. Then for each of the seven factors, numeric criteria are specified and according to specified criteria, the primary maps are prepared and classified. Finally, the classified maps are analyzed and overlapped using Boolean logic. In the second part of the model, GIS output is considered by probit and logit random models.

First stage - Geographic model

Concerning the mentioned issues some criteria have been determined for the classification of each geographical factor Table 1.

These criteria for each factor are provided from various resources such as the instructions of the ministry of mines and industries for establishing new industrial units, rules and standards for establishing industries ratified by the government, the act of preventing underground waters contamination and the act of maintaining the territory of the road ratified by the ministry of roads and transportation. For the map of ground slope and altitude, the earth digital altitudinal map is prepared and extracted concerning the coordinates of the studied geographical boundary (the country's geographical boundary by taking into account the international boundaries) and then the ground slope map and altitude map are generated based on this map and using geographical information system and ArcMap software.

In this study, the Boolean logic model is employed for overlapping the maps. Scoring the geographical criteria based on Boolean logic is demonstrated in the below Table 2. All the primary maps are rasterized and should convert to vector maps to perform the overlapping operation and employ Boolean logic and then apply overlapping and aggregation operation on them.

Finally, the information layer resulting from overlapping the classified layers is inserted into the GIS environment and the final calculation is performed using Boolean logic and AND operand. The final output indicates the regions in which all information layers are suitable for establishing an oil refinery. According to the output map Bojnourd, Ilam, shahrekord, yasooj and sanandaj cities don't have the necessary geographical (qualifications) for establishing an oil refinery.

Finalizing the selected regions

After obtaining the final output, some regions should be omitted from the final map for the following reasons:

- Based on Act 1346/03/20 and report No. M/628 of the ministry of economy, Council of Ministers and environment conservation organization, establishing the industries in Tehran and its suburban areas is prohibited up to the range of 120 kilometers. Therefore Due to this Act, the selected regions of the geographical system with the mentioned characteristics will be omitted from the final output.

- Based on the Act of Council of Ministers No. H18591T/64677 date of 1378-12-26 establishing the industries up to the radius of 50 km is prohibited in Isfahan.

Therefore Due to this Act, the selected regions of the geographical system with the mentioned characteristics will be omitted from the final output.

- Based on Act 2 Note No. H25842T/Date of 1381/07/16 establishing chemical industries having industrial sewage in their production process is prohibited in Gilan, Mazandaran and Golestan provinces. Therefore, Due to this Act, selected areas of geographical information systems in mentioned provinces will be omitted from the final output. So concerning the mentioned Acts, parts of the selected regions of the geographical information system have been omitted from the final output.

Second stage – Econometric models of Logit and Probit

After investigating the geographical factors influencing the location problem by geographical information system and determining the regions suitable for establishing oil refinery, in the second stage economic and quantitative factors are taken into account and a combinational model will be developed for location problem. The model used in this study will be as follows.

Equation 1

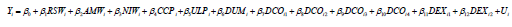
Theoretical expectation sign and the explanations of each of the variables in the model are given in Table 3.

The dependent variable Y takes two values of zero and one. Thus, for 30 centers of the province (city) under study, 8 cities have refineries, the dependent variable Y is one and for the remaining 22 centers of the province is zero. In this study, four areas have been considered for the supply of raw materials: khark, lavan, siri, Bahregan. Therefore, the variable of distance from the place of supply of raw materials is as Table 4.

Concerning the statistics of oil ministry and national oil products Distribution Company, a major share of the products are exported to other countries through international markets. Therefore the establishment of an oil refinery should occur in a place that needs minimum transportation cost for exporting oil products to neighboring countries. In our studied model, the main oil products exporting ports are regarded as output points and sale markets. Oil products sales and exports are mainly carried out through the Persian Gulf marine boundaries including Mahshahr and Bandar Abbas ports. So the variable of ith location distance from the exporting sales markets would be as follows:

DEX_i1: Distance of the place i to Bandar Abbas

DEX_i2: Distance of the place i to Mahshahr

Estimation of model

In this section, the model estimation and results interpretation are presented using the information provided in the variable description section. Eviews were employed for Model estimation both with logit and probit models to compare the results. In all estimation results tables, LOGL value and coefficients statistics are reported in addition to independent variables coefficients so that fitting and interpretation of results can perform as well and proportion of the variations described by the descriptive variables are determined. Also, to evaluate the proper fit of the model, the Hassmer-Lemshou fit test was used. In the first stage of estimation, all variables are inserted into the model in logarithmic form and distance variables are inserted in simple and square forms due to the colinearity problem. Distance from the location of raw material supply is inserted in simple form and distance from exporting market in square form (Table 5).

In initial estimation, it is observed that none of the coefficients are significant in 95 percent confidence level and only DUMi and LOGNIW; coefficients are significant in 90 percent confidence level. The coefficients of LOGAMWi, OCOi and LOGCCP are opposite to their expected signs as presented in theory but other variables had the expected sign. This indicates that model structure has mistaken and as a result, it arises problems in model empirical results. Although it should be noted that these mistakes in the model structure are due to the facts in the real world over the studied period. For instance, oil fields and also oil products exporting ports are located in southern regions of the country. This concentration results in a severe co-linearity between distance variables which have some effects on the model results such as coefficients insignificance.

In the second stage, firstly LOGCCPi is transformed from logarithmic form to simple form and is inserted into the model. By performing this operation, the sign of oil products per capita consumption variable will be the same as the theory. On the other hand concerning the results, it is observed that the model significance level has been notably increased; which effects could be observed in Z statistic of variables such as virtual variable of the local sales market, variable of the number of industrial zones available in provinces capitals and also other variables. In this estimation, the sign of LOGAMW; and DCOi variables are opposite to the expected sign in the theory.

In the last stage, by omitting two variables of CCPi and LOGRSWi from the model all coefficients have the same sign as the theory. So after this stage concerning the appearance of all variables in the model with the same sign as the theory, the model significance level should be increased by change of variables. In this stage the land price variable could be omitted for the following reasons:

- During the three stages of model estimation z statistic value for land price variable has decreased by every stage and the significance level of this variable has decreased with different estimations.

- In the establishment of an oil refinery, the price of the land required for building an oil refinery is less important than other variables in the model since The land cost is a part of initial investments but the costs such as transportation costs in distance variables and/or sales markets or labor costs are parts of current costs which optimizing these costs results in the increase of income in long term. On the other hand, since the oil industry in Iran is governmental and also the refineries are located in suburban areas, land price is not very important in the study of establishing a refinery as a governmental and fundamental industry. The reason is that purchasing the lands in suburban areas (which is in the possession of the government) has the least cost for setting up refineries as the industrial infrastructure of the country. Therefore the variable of distance from raw material supply location is so in the fourth stage urban land price variable is omitted from the model.

In this stage in both logit and probit estimations, the signs of model variables are the same as the theory signs. In this estimation it is observed that the significance of the coefficients has increased compared with the previous state and the signs are as it is expected. But regarding the significance of distance variables coefficients, the main reason is the extreme co-linearity between these variables. This colinearity has been ordinary because both oil products exporting ports and the oil fields applying the raw material for an oil refinery are located in southern regions of the country. By changing the form of distance variables in this stage, a significance level of the remaining variables in the model can be increased up to also higher level, such that in the fifth stage, instead of DCOi its square form, DCOTWOi, is used.

The stages of changes in the model variables (Remove variable or deform from logarithmic mode to simple and vice versa) until reaching the final model are described in Table 6.

It is observed that the coefficients of LOGNIWi, LOGAMWi and DUMi in logit model estimation are significant in 96 percent confidence level and probit model in 97 percent confidence level. But the coefficients of distance variables are still small and insignificant. Since the results obtained in this stage have an acceptable percent of principle variables significance and also have the expected signs and on the other hand distance variables insignificance is due to the high collinearity between these variables, current results are applicable where the objective is limited to calculation of the probability of different locations. Table 7 shows these probabilities and also the ranking of the studied locations using the fourth stage estimation (Table 8).

It should be noted that in logit models, to study the model significantly, the R² statistic cannot be used. For this reason, to test the goodness of fit at this stage, the Hammer-Lemshou statistic has been used, the value of this statistic is equal to 12.35 and the probability is 0.1361, which indicates a proper fit by the logit model.

To calculate the probabilities at first Y_i is calculated and then by replacing Y_i in the following relation P_i is obtained =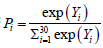

More over the following relation is used to calculate the effect of a change on descriptive variables:

Now it is possible to interpret coefficients of Table 9 which were the basis for the first stage of ranking. For instance, the coefficient of LOGNIWi variable indicates that assuming other conditions and variables are fixed (unchanged), whenever the number of industrial zones in a province capital increases by one percent, the chance of selecting that location (province Capital) for establishing an oil refinery (with more than 95% confidence) will increase by 3.938 percent and the probability of selecting that province capital will increase by 3.938 pi (1-Pi).

It should be noted that in each case, the extent of probability fluctuations per variation in the independent variable is a fraction of Pi which means that increase and decrease in the probability of selection depend on the location which is being studied. In other words, an increase in labor wage in a location (for example Yazd) may have a different effect than the same increase in labor wage in another location (for example Ilam). This is very important and is indicative of a model's ability to consider special conditions of locations.

Table 8 shows the ranking concerning the results from the first stage of the model. The results of ranking indicate that of 9 existing refineries in Iran 6 refineries of Isfahan, Fars, Khozestan, Markazi, Tehran and Kermanshah are in the first to sixth ranks which is indicative of the optimized establishment patterns in these 6 refineries. Tabriz refinery located in Eastern Azarbaijan province is in 13^th rank and Bandar Abbas refinery located in Hormozgan province is in 20^th rank which shows non-optimized establishment patterns in these two refineries.

By omitting the locations that have refineries and also the province capitals which don't have the qualifications for the establishment of an oil refinery in geographical information system, resultant ranking in this stage is demonstrated in the Table 7. In this ranking, Yazd city has the first place rank as the optimal location.

To have a more accurate model (in terms of coefficients significance) one of the distance variables will be omitted from the model since it is not statistically significant. So by omitting the DEXTWOi variable, the estimation results in the fifth stage will be as (Table 9).

It is observed that all coefficients in the logit model are significant at 97 percent confidence level and in the probit model at 98 percent confidence level and all coefficients have the same signs as the theory. But the coefficient for the variable of distance from raw material supply location still has a small value which indicates that the distance variable has a weak effect on the probability of selecting a location for establishing an oil refinery. Table 10 shows the final ranking of province centers (after omitting the centers that have refineries and the centers that are omitted in the geographical information system) based on the estimation results of the sixth stage (Table 10).

Results Interpretation and Discussion

Of 8 variables presented in the econometric model section (the ratio of skilled Industrial employees to all employees in a region, average monthly wage in a region, the number of industrial zones in a region, per capita consumption of oil products in a region, land price in a region, the presence or absence of local markets in a region, distance from raw material supply location and distance from foreign sales markets) four variables (the number of industrial zones in a region, average monthly payment in a region, the presence or absence of local markets in a region and distance from raw material supply location) are significant in the final model and the coefficients of the mentioned variables are the same as the theory. Whit regard to the results of Table 8 Yazd city is in the first place and Bushehr city is in second place. These results show that building an oil refinery in yazd city is an optimal decision. Establishing an oil refinery in this city leads to an optimized result concerning the capability of transporting oil products to the eastern regions of Iran. National oil products distribution companies afford very high costs for oil products transportation to central regions such as kerman and Yazd due to the lack of refineries in these regions. This result of the model is indicative of appropriate real-world estimation. Mashhad, zangan and Semnan cities are among the other eastern cities which need oil refineries and are in the sixth to 8th places, respectively.

The results of Table 10 which have been obtained based on solving the model by omitting the variable of distance from the exporting ports(which is applicable in term of internal and local oil products demand) has made changes in cities rankings. For example, the rank of Bushehr city has changed from second place to first place and Yazd city has obtained second place. In both rankings, Zahedan, Birjand and Ardebil cities have the last ranks in priority of establishing an oil refinery.

In both rankings, Qom and Khorambad cities are among the first six priorities. Based on the previous studies conducted on the cost of oil products transportation, it recommends that to cut transportation costs dramatically in national oil products refinement and distribution companies, the capacity of the Arak refinery should be increased this issue has been considered in this study by establishing refineries in Qom and Khoramabad cities which have the least distance from Arak refinery.

Conclusion

In the process of locating an oil refinery site four factors (labor wage, the number to industrial zones, distance from raw material supply location and the presence of local sale markets) are effective. Based on Hansen’s location theory, the external economy of concentration is an important factor in locating. Which in this study the variables of local sale markets and the number of industrial zones support this fact? Moreover based on Hansen's theory the land price variable is insignificant in locating which is validated in this study.

The optimized pattern suggested in this study resolves the problems related to the high transportation costs of oil products for delivering to the eastern regions and provinces (due to the lack of refineries in these regions).

References

1. Yang, Yang, Kevin K.F Wong and Tongkun Wang. "How do hotels choose their location? Evidence from hotels in Beijing." Int J Hosp Manag 31(2012): 675-685.

Google Scholar, Crossref

2. Küçükaydin, Hande, Necati Aras and I Kuban Altınel. "Competitive facility location problem with attractiveness adjustment of the follower: A bi-level programming model and its solution." Eur J Oper Res 208 (2011): 206-220.

Google Scholar, Crossref

3. Miller, Tan C, Terry L Friesz and Roger L Tobin. “Equilibrium facility location on networks.” Springer Sci Rev (1995).

Google Scholar, Crossref

4. Bhadury, Joy, Horst A. Eiselt and Jorge H Jaramillo. "An alternating heuristic for medianoid and centroid problems in the plane." Comput Oper Res 30 (2003): 553-565.

Google Scholar, Crossref

5. Drezner, Zvi. "Competitive location strategies for two facilities." Reg Sci Urban Econ 12 (1982): 485-493.

Google Scholar, Crossref

6. Plastria, Frank and Lieselot Vanhaverbeke. "Discrete models for competitive location with foresight." Comput Oper Res 35 (2008): 683-700.

Google Scholar, Crossref

7. Labbé, Martine and S Louis Hakimi. "Market and locational equilibrium for two competitors." Oper Res 39 (1991): 749-756.

Google Scholar, Crossref

8. Lederer, Phillip J and Arthur P Hurter Jr. "Competition of firms: Discriminatory pricing and location." Econometrica (1986): 623-640.

Google Scholar, Crossref

9. Lederer, Philip J and Jacques-François Thisse. "Competitive location on networks under delivered pricing." Oper Res Lett 9 (1990): 147-153.

Google Scholar, Crossref

10. Sarkar, Jyotirmoy, Barnali Gupta and Debashis Pal. "Location equilibrium for Cournot oligopoly in spatially separated markets." J Reg Sci 37 (1997): 195-212.

Google Scholar, Crossref

11. Wendell, Richard E and Richard D. McKelvey. "New perspectives in competitive location theory." Eur J Oper Res 6 (1981): 174-182.

Google Scholar, Crossref

12. Rhim, Hosun, Teck H. Ho and Uday S. Karmarkar. "Competitive location, production, and market selection." Eur J Oper Res 149 (2003): 211-228.

Google Scholar, Crossref

13. Pérez, María Dolores García, Pascual Fernández Hernández, and Blas Pelegrín Pelegrín. "On price competition in location-price models with spatially separated markets." Top 12 (2004): 351-374.

Google Scholar, Crossref

14. Berman, Oded and Dmitry Krass. "Locating multiple competitive facilities: spatial interaction models with variable expenditures." Ann Oper Res 111 (2002): 197-225.

Google Scholar, Crossref

15. Drezner, Tammy and Zvi Drezner. "Validating the gravity-based competitive location model using inferred attractiveness." Ann Oper Res 111 (2002): 227-237.

Google Scholar, Crossref

16. Drezner, Tammy, Zvi Drezner and Said Salhi. "Solving the multiple competitive facilities location problem." Eur J Oper Res 142 (2002): 138-151.

Google Scholar, Crossref

17. Drezner, Tammy and Zvi Drezner. "Finding the optimal solution to the Huff based competitive location model." Comput Manag Sci 1 (2004): 193-208.

Google Scholar, Crossref

18. Drezner, Tammy and Zvi Drezner. "Multiple facilities location in the plane using the gravity model." Geogr Anal 38 (2006): 391-406.

Google Scholar, Crossref

19. Drezner, Tammy and Zvi Drezner. "Lost demand in a competitive environment." J Oper Res Soc 59 (2008): 362-371.

Google Scholar, Crossref

20. Fernández, José, Blas Pelegrı, Frank Plastria and Boglárka Tóth, et al. "Solving a Huff-like competitive location and design model for profit maximization in the plane." Eur J Oper Res 179 (2007): 1274-1287.

Google Scholar, Crossref

21. Aboolian, Robert, Oded Berman and Dmitry Krass. "Competitive facility location and design problem." Eur J Oper Res 182 (2007): 40-62.

Google Scholar, Crossref

22. Fernández, José, Blas Pelegrín, Frank Plastria and Boglárka Tóth, et al. "Planar location and design of a new facility with inner and outer competition: An interval lexicographical-like solution procedure." Netw Spat Econ 7 (2007): 19-44.

Google Scholar, Crossref

23. Tóth, Boglárka, José Fernández, Blas Pelegrín and Frank Plastria, et al. "Sequential versus simultaneous approach in the location and design of two new facilities using planar Huff-like models." Comput  Oper Res 36 (2009): 1393-1405.

Google Scholar, Crossref