2021 Conference Announcement - (2024) Volume 9, Issue 7
Received: 26-Sep-2022, Manuscript No. jbbs-23-87910;
Editor assigned: 28-Sep-2022, Pre QC No. P-87910;
Reviewed: 12-Oct-2022, QC No. Q-87910;
Revised: 18-Oct-2022, Manuscript No. R-87910;
Published:
26-Oct-2022
, DOI: 10.37421/1736-4337.2020.14.302
, QI Number: 1
Citation: Imbalzano, Marco. â??Making Use of Machine Learning Algorithms for Multimodal Equipment to Assist in COVID-19's Assessment.â? J Bioengineer & Biomedical Sci 12 (2022): 325.
Copyright: © 2022 Imbalzano M. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Sources of funding : 1
Differentiation • Geometry • Calculus • Trigonometric functions
This perspective is about the chain rule in differentiation. For other uses, see Chain rule (disambiguation). In calculus, the chain rule is a formula to compute the derivative of the functional composition of two or more functions [1-3]. The chain rule provides us a technique for finding the derivative of composite functions, with the number of functions that make up the composition determining how many differentiation steps are necessary [4-7]. The chain rule has broad applications in physics, chemistry, and engineering, as well as being used to study related rates in many disciplines. The chain rule can also be generalized to multiple variables in cases where the nested functions depend on more than one variable [8-11]. Now we may go further to our claim in this perspective mentioned in abstract. Inverse of multiple functions and then finding the differentiation with our all possible prospects through chain rule along with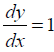 
.
If multiple functions are there in one and another so finding the derivative would like be as follow:
Y=f(x(u(v)))
……. (1)
Here this can also be written as with many prospects by changing the sequences as follow:
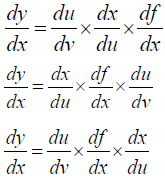
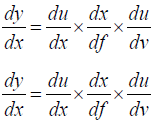
Now we got all prospects and these are liable to find the differentiation of y with respect to x and note that the 1st prospect can also called as Inverse of chain rule formula. Now implementing it in inverse of multiple functions as follow:
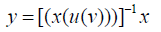
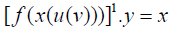
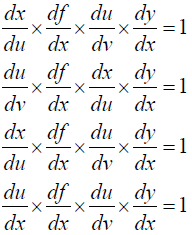
Firstly: Here my perspective paper’s claim is completed. i.e. If we go on changing the sequences in the chain rule of calculus and, then formed the many prospects. Secondly, Implementing them in Inverse of multiple functions, and then finding the differentiation with our all possible prospects through chain rule along with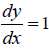 
. [11-15]
In order to get the more clarifications about the Inverse of multiple functions here is a solved example with Inverse of chain rule formula as follow:
1) 
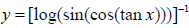
Now find the differentiation with our prospects as follow:
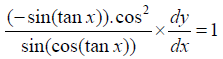
2) 
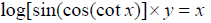
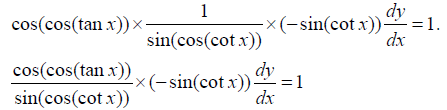
3) 
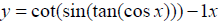
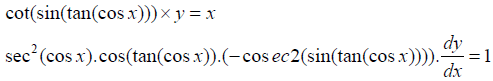
Similarly further prospects can be solved for any of the multiple functions [15-20].
I conclude that this is perspective paper and the claim of ours was only to show the possible prospects, inverse of multiple functions chain rule to the world and the differentiation is=1. I hope so this is going to give a direction to the branch of calculus.
This work is a self-research and supported by the author itself.
