On Further Application of the Generalized Vectorial Laws of Reflection and Refraction to Solve a Novel Problem in Geometrical Optics

Pramode Ranjan Bhattacharjee^*
*Correspondence: Pramode Ranjan Bhattacharjee, Department of Physics, Kabi Nazrul Mahavidyalaya, Agartala, India, Email:

Keywords

Refection and refraction of light • Generalized vectorial laws of reflection and refraction • Vector algebra and vector calculus • Determinantal equation • Cartesian coordinate geometry

Introduction

Development of determinantal equations in cases of reflection and refraction of light [1-4] has been carried out by the author earlier. In, an effort has been made to generate novel determinantal equations by making use of the coordinates of the object point, point of incidence, and the point of observation with simultaneous use of the equation of the reflecting or refracting surface on the basis of the generalized vectorial laws of reflection and refraction [5]. Along with presenting novel approaches for the solution of some problems in geometrical optics, the said generalized vectorial laws of reflection and refraction have been employed further in for the development of novel determinantal equations with involvement of the coordinates of the object point, image point, and the point of incidence making simultaneous use of the reflecting or refracting surface. With the presentation of a novel algorithm, generation of novel determinantal equations involving the coordinates of the object point, point of incidence, point of observation, and the image point in cases of reflection and refraction of light has also been accomplished in [3]. A similar attempt has also been made in in respect of developing determinantal equations involving the Cartesian coordinates of the object point, image point and the point of observation in relation to reflection and refraction of light at plane as well as spherical reflecting and refracting surfaces.

In order to enrich the optical physics literature to a further extent, working in line with the aforesaid group of works, this paper discloses the solution of the following problem. Is it possible to involve the Cartesian coordinates of the image point, point of incidence, and the point of observation in case of reflection (refraction) of light to give birth to determinantal equations? This problem is equivalent to that of finding the condition of collinearity of three points having Cartesian coordinates (α₁, β₁, γ₁), (α₂, β₂, γ₂), (α₂, β₂, γ₂) provided that those three points correspond to the image point, point of incidence, and the point of observation respectively. Thus the problem considered in this paper differs from the traditional problem of finding the condition of collinearity of three given points (α₁, β₁, γ₁), (α₂, β₂, γ₂), (α₂, β₂, γ₂) in Cartesian coordinate geometry in which those three points may lie anywhere in space and no additional restriction has been imposed in regard to their actual position or location.

In order to arrive at the desired goal, the generalized vectorial laws of reflection and refraction developed in 2005 have been used along with making simultaneous use of the well-known concept of “Gradient of a scalar point function” in Vector calculus and elementary concepts of Vector algebra. Two different conditions of collinearity, one in case of reflection and the other in case of refraction, have been developed and each such determinantal equation representing the condition of collinearity of the image point, object point, and the point of observation is novel. The problem addressed is also novel and unlikely to be found in the optical physics literature [6-8].

Materials and Methods

The novel problem

The problem addressed in this paper, which has never been found to have been dealt with in the optical physics literature, could be put in the following form.

Is it possible to involve the Cartesian coordinates of the image point, point of incidence, and the point of observation when reflection (refraction) of light takes place from a plane (curved spherical) reflecting (refracting) surface to give birth to determinantal equation by making use of the generalized vectorial laws of reflection and refraction reported in 2005?

The solution of the aforesaid problem has been accomplished in the subsequent section with the help of the generalized vectorial laws of reflection and refraction and making use of elementary knowledge about vector algebra and the concept of “Gradient of a scalar point function” in Vector calculus [9,10].

Solution of the novel problem

Case 1: The case of reflection by a plane reflecting surface.

To deal with this case for arriving at the desired goal, let us confine to the diagram shown in Figure 1. With reference to an arbitrary three dimensional rectangular Cartesian coordinate system, let us first assign the Cartesian coordinates of the image point P, point of incidence Q, and the point of observation G as (α₁, β₁, γ₁), (α₂, β₂, γ₂), (α₂, β₂, γ₂) respectively. Also, with reference to the same system of coordinates, let the equation ax+by+cz+d=0 of the plane reflecting surface be given by: ax+by+cz+d=0 where all of a, b, c, and d are scalar constants. This equation of the plane reflecting surface can be written φ(x,y,z)=ax+by+cz+d=0, where is a scalar point function.

From the physical significance of “Gradient of a scalar as point function”, it then follows that

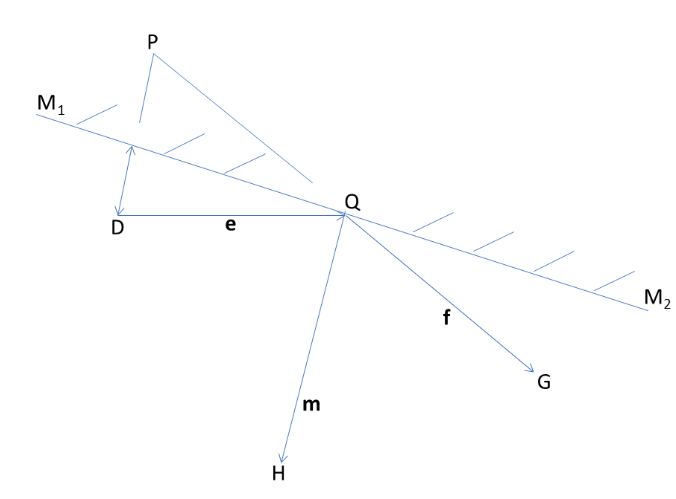
Diagram showing reflection of light by a plane mirror M₁ M₂ in which D is the object point; Q, the point of incidence; G, the point of observation; QH, the normal to the reflector at the point of incidence; P, the image point corresponding to the object point D; e, f, and m, the unit vectors along the directions of the incident ray, reflected ray, and the positive normal to the plane mirror at the point of incidence respectively

Now, it can be readily seen by considering Figure 1 that the following three different expressions for the unit vector f along the direction of the reflected ray are possible.

Making use of the relations (1) and (2), (1) and (3), and (1) and (4) in succession, it is then possible to arrive at the following three relations one after another with the help of the generalized vectorial law of reflection, which is: m × e= m × f.

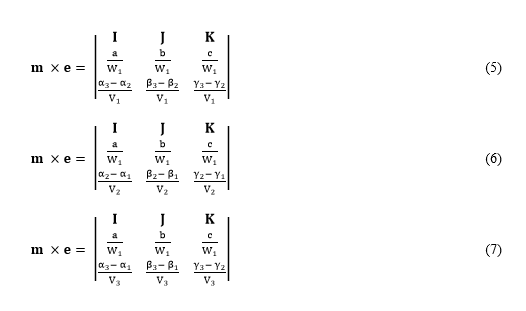
Now, eliminating (m × e) from the relations (5) and (6) and comparing corresponding coefficients of I, J, and K on both sides of the eliminant, it is then easy to see that the following three equations could be developed.

Then eliminating V₁/V₂ from the above equations (8) and (9), (9) and (10), and (10) and (8) in succession, it is then easy to verify that the final result in each case will be the following determinantal equation.

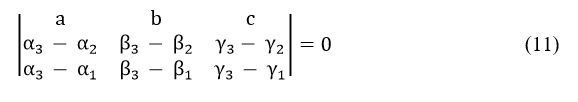
If the same procedure is repeated by considering the equations (6) and (7), as well as the equations (7) and (5) in succession, it could be possible to arrive at the following two other determinantal equations.

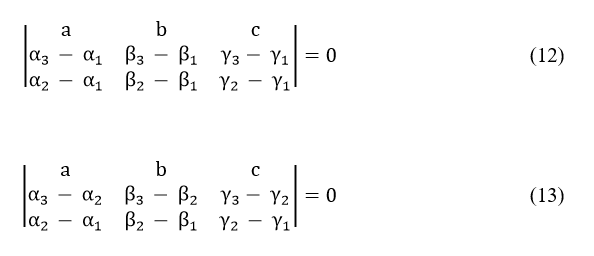
Now that the three determinantal equations (11), (12), and (13) will have to be valid simultaneously, we must have

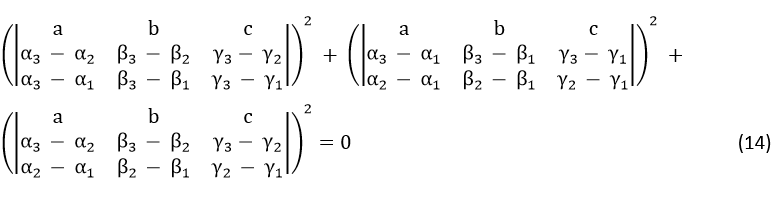
Equation (14) is then the resultant determinantal equation for this particular case of reflection of light by a plane mirror. In other words, equation (14) represents the condition of collinearity of the points (α₁, β₁, γ₁), (α₂, β₂, γ₂), (α₂, β₂, γ₂) subject to the constraint that they are the Cartesian coordinates of the image point, point of incidence, and the point of observation respectively, when reflection of light takes place from a plane reflecting surface, the equation of the plane surface of the reflector being ax+by+cz+d=0.

Note 1: Considering relevant diagram and the generalized vectorial law of refraction, it can be easily verified by making use of the aforesaid procedure that the same determinantal equation (14) will also result while dealing with the case of refraction at a plane surface of discontinuity irrespective of whether light travels from a rarer medium to a denser medium or from a denser medium to a rarer medium.

Results and Discussion

Case 2: The case of reflection by a concave spherical reflecting surface

To deal with this case, let us consider Figure 2. In order to avoid the tedious steps of algebraic calculations, let us now consider an arbitrary right-handed system of coordinates having its origin located at the centre of curvature of the concave spherical reflecting surface and let us assume that the Cartesian coordinates of the image point P, point of incidence Q, and the point of observation G with respect to the said system of coordinates be (α₁, β₁, γ₁), (α₂, β₂, γ₂), (α₂, β₂, γ₂) respectively. With reference to the same system of coordinates, the equation of the concave spherical surface can be taken as:

x²+y²+z²=r² , where r is the radius of curvature of the concave spherical surface and is a scalar constant for the particular reflecting surface under consideration.

The above equation of the concave spherical reflecting surface can be put in the form ψ(x,y,z)=x²+y²+z² -r²=0, where ψ(x,y,z) is a scalar point function.

Then the expression for the unit positive normal vector m at the point of incidence (α², β², γ²) can be obtained as:

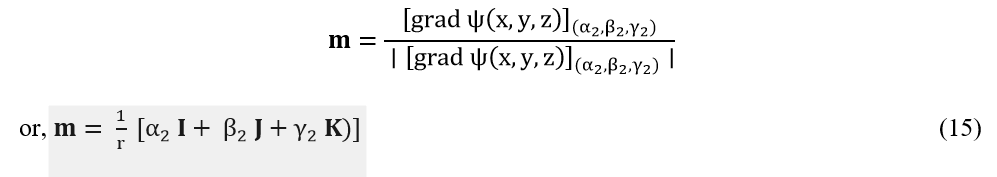
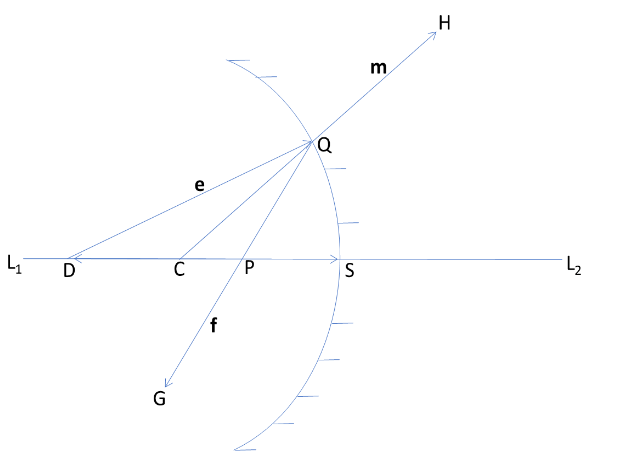
Figure 2. Diagram showing reflection of light by a concave spherical mirror in which S is its pole; C, the centre of curvature; L1 L2, the principal axis; D, the object point; Q, the point of incidence; G, the point of observation; QH, the normal to the reflector at the point of incidence; P, the image point corresponding to the object point D; e, f, and m, the unit vectors along the directions of the incident ray, reflected ray, and the positive normal to the reflector at the point of incidence respectively.

Considering Figure 2, the following three different expressions for the unit vector f along the direction of the reflected ray are possible.

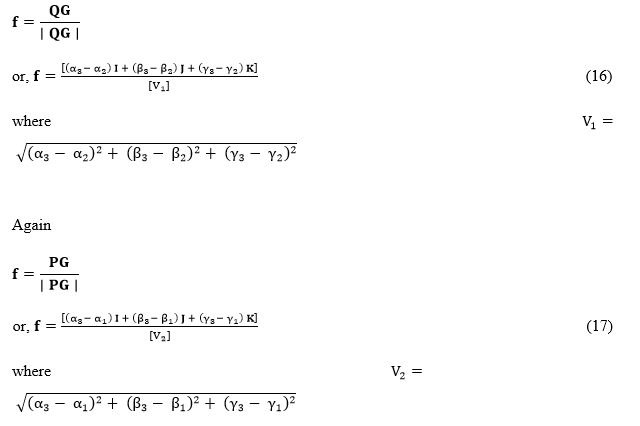
As before using the relations (15) and (16), (15) and (17), and (15) and (18) in succession, it is then possible to arrive at the following three relations one after another with the help of the generalized vectorial law of reflection, namely, m × e=m × f.

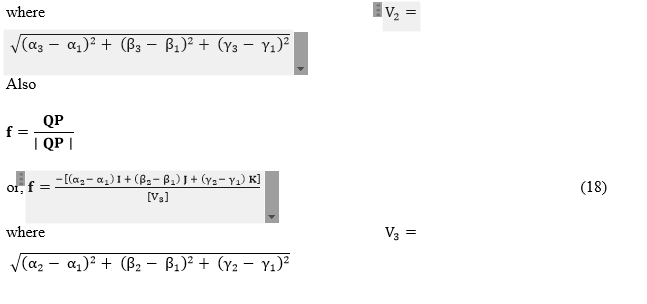
Now, eliminating (m × e) from the relations (19) and (20) and comparing corresponding coefficients of I, J, and K on both sides of the eliminant, it is then easy to see that the following three equations could be developed.

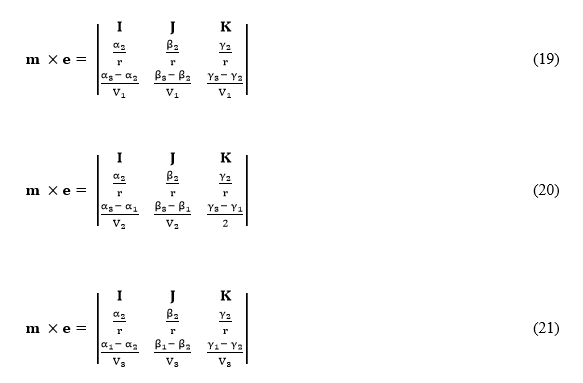
Then eliminating V₁/V₂ from the above equations (22) and (23), (23) and (24), and (22) and (24) in succession, it is then easy to verify that the final result in each case will be the following determinantal equation.

Now, eliminating (m × e) from the relations (20), (21) and (19), (21) in succession and applying the same procedure for each case, it can be readily seen that the following determinantal equations could be developed for those two cases.

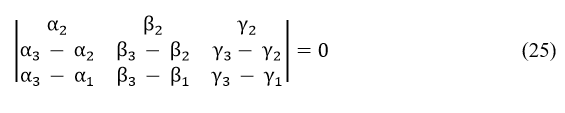
Now that the three determinantal equations (25), (26), and (27) are to be valid at a time, it follows that the resultant determinantal equation for this particular case of reflection by a concave spherical mirror will be given by

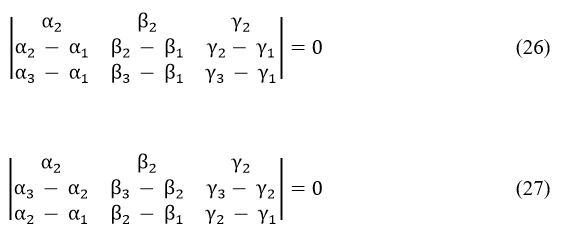
Equation (28) represents the required determinantal equation for this particular case of reflection.

Note 2: By considering relevant diagram (or Figure) for each of the cases of reflection by a convex mirror and refraction at a concave (or convex) refracting surface regardless of whether light moves from a rarer medium to a denser medium or from a denser medium to a rarer medium, the same procedure based on the generalized vectorial laws of reflection and refraction, may be applied to arrive at the same determinantal equation (28).

Conclusion

As an extension of the application of the generalized vectorial laws of reflection and refraction reported in 2005, this paper addresses the solution of an interesting problem falling within the purview of geometrical optics. Such a problem has never been addressed in the field of optical physics and hence the problem considered in this paper is entirely novel. The problem considered is to find the condition of collinearity of the image point, point of incidence, and the point of observation in case of reflection (refraction) of light when the Cartesian coordinates of those three points as well as the equation of the reflecting (refracting) surface are known with respect to an arbitrary right-handed Cartesian coordinate system. Such a problem differs from the traditional problem of finding collinearity of three given points in three dimensional Cartesian coordinate geometry in that, in the present case, the three points, namely the image point, point of incidence, and the point of observation are very much linked with the case of reflection and refraction, but there is no such restriction exists on the three points in three dimensional Cartesian coordinate geometry for dealing with the problem of finding collinearity of three given points.

The resultant determinantal equations (14) and (28) developed in this paper could now be placed into context to the condition of collinearity of three given points and which can be obtained from the expression for the area of a triangle formed by three given points in three dimensional space as:

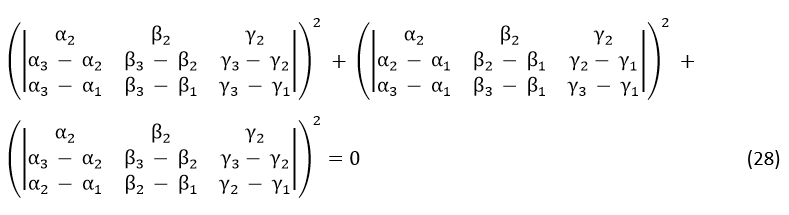
It may be noted that equations (14) and (28) are totally different from equation (29). This is because in the condition of collinearity given by equation (29), no additional conditions are imposed on the three given points (α₁, β₁, γ₁), (α₂, β₂, γ₂) and (α₃, β₃, γ₃). As a result, this condition of collinearity expressed by equation (29) will be applicable irrespective of the position or location of those three given points. But in the determinantal equations (14) and (28), the three points (α₁, β₁, γ₁), (α₂, β₂, γ₂) and (α₃, β₃, γ₃) are closely related to the corresponding case of reflection or refraction considered for the derivation of such a determinantal equation. Furthermore, in each such process of derivation, the point of incidence  (α₂, β₂, γ₂)  should have to lie either on the plane reflecting (refracting) surface defined by the equation ax+by+cz+d=0, or on the curved reflecting (refracting) surface defined by the equation x²+y²+z²=r² . Thus each of the determinantal equations (14) and (28) could be treated as the condition of collinearity of the said three points when some additional constraints as stated above are imposed on them.

The determinantal equations developed are interesting, novel and original. The material incorporated in this paper are likely to enrich the optical science literature and at the same time it will have academic and educational importance as well.

References

1. Bhattacharjee, Pramode Ranjan. "The generalized vectorial laws of reflection and refraction leading to the development of novel equations involving the coordinates of the source point, point of observation, and the point of incidence." Optik 218 (2020): 164988.

   [Crossref] [Google Scholar]

2. Bhattacharjee, Pramode Ranjan. "Addressing a novel problem on the basis of the generalized vectorial laws of reflection and refraction along with offering novel treatments of derivation of some results in geometrical optics." Optik 261 (2022): 169113.

   [Crossref] [Google Scholar]

3. P. R. Bhattacharjee. “On finding determinantal equations involving the coordinates of the object point, point of incidence, point of observation and the image point in cases of reflection and refraction.” J Phys Opt Sci (2022).

   [Crossref]   

4. P. R. Bhattacharjee. “Involving the Cartesian coordinates of the object point, image point, and the point of observation to give birth to novel determinantal equations in cases of reflection and refraction of light.” J Phys Chem Res (2023).                                        
5. Bhattacharjee, Pramode Ranjan. "The generalized vectorial laws of reflection and refraction." Eur J Phys 26 (2005): 901.

   [Google Scholar]

6. A. W. Barton. “A Text Book on Light.” (1939).
7.  Southall, James Powell Cocke. “Mirrors, prisms and lenses: A text-book of geometrical optics.” (1923).
8. E. Hecht. “New York: Pearson.” (2017).
9.  P. R. Bhattacharjee. “Giving Birth to Vectorial Coordinate Geometry ll.” 4 (2019). [Crossref] [Google Scholar]
10. Spiegel. “Murray R. Schaum's outline of theory and problems of vector analysis and an introduction to tensor analysis.” (1974).  

    [Google Scholar]