Modelling the Effect of Depletion Rate of Forestry Resources due to Industrialization on the Effect of Population and Population Augmented Industrialization on Forestry Resources

Jonathan Ezeorah^1* and E N Ekaka-A^2
*Correspondence: Jonathan Ezeorah, Department of Mathematics, University of Calabar, Calabar, Nigeria, Tel: 2348033553665, Email:

Keywords

Stability • Forest resource biomass • Simulate

INTRODUCTION

In the last thirty years, several remarkable researches have been made towards understanding how the decrease in biodiversity affects the functioning of the ecosystem and its effect on human lives. It is an established fact that biodiversity promotes the efficiency by which ecological communities get their resources, produce biomass and recycle essential nutrients [1]. It is a known fact that biodiversity increases the stability of ecosystem processes in changing environment but the stability of this ecosystem has been threatened seriously by the activities of human beings on the forestry resources. The main reason for this is food and development. Proliferation of both wood- based and non-wood based industries has brought about incessant attack on forestry resources. The stability of the biodiversity has been threatened and the effect has been shown in the climate change [2].

In 2015 Misra and Lata proposed and analyzed a mathematical model to study the depletion and conservation of forest biomass in the presence of industrialization. In their model, they assumed that industrialization increase where there is enough forest biomass and the intrinsic growth rate and carrying capacity of the forest biomass depend on industrialization and technological effort. The model also showed that increase in carrying capacity due to technological efforts has a destabilizing effect. Numerical simulations were also performed to confirm the analytical results [3]. Mathematical model for the degeneration and regeneration of forest resources. The dynamic model showed that the effect of industrialization on the reduction of forest biomass and the effect of regeneration on the model which allows for the model sustenance. In study of the depletion of forestry resource biomass that has been attributed to crowding by industrialization using the technique of a nonlinear mathematical model showed that the density of the forest biomass would decrease as the crowding by industrialization increase [4].

Robert in their research the role of population in developing countries concluded that pressure on forestry resources in developing countries arising from population growth are often covered or complicated by the rise in market demand of the resources, poverty and poor management of forestry resources. They illustrated this with a variety of data and a simulation model of resource management. In their model showed the effects of industrialization and associated pollution on forestry resources [5]. The assumption here was that both wood and non-wood-based companies coexist in the forest habitat and both generate pollution which also affects the forest resources. While wood-based company depends on forest resources, there is a constant rate of resources which does not depend on the forest that is provided to the non-wood company. The stability theory of differential equation and numerical simulation are used in the analysis of their model. The result of their research showed that increase in woodbased companies decreases the forest resources and also increase in non-wood-based industries decreases the forest resources too. They concluded that forest resources may go into extinction if pollution from both wood and non-wood-based companies are not well checked [6].

A mathematical model to study the growth and existence of resource-biomass-dependent species in a forested habitat which is being depleted due to increase in industrialization. The model showed that increase in industrialization decreases biomass density thereby decreasing the density of species which may go into extinction if not well handled. The model encouraged control measure to ensure the survival of resource-biomass-dependent species. In their paper proposed a nonlinear dynamic model to study the survival of biological species in a polluted environment [7]. Environmental tax is considered in the model to be a measure of improving environmental quality. By using suitable Lyapunov function, local and nonlinear stability conditions are obtained. It was shown that increase in pollution brings decrease in the density of the biological species. It was also shown that environmental tax plays a major role in controlling the concentration of pollutant in atmosphere thereby maintaining the concentration of the biological species. They proposed and analyzed a nonlinear mathematical model which studies the formation of acid rain in the atmosphere due to precipitation and the effect on plant species [8,9].

They stated that acid-forming gases like SO₂ and NO₂ emitted from various sources combined with moisture and form acid rain which affects the forest biomass. The model was analyzed using stability theory of differential equations and numerical simulation. The result shows that increase in acid rain decrease the density of biomass plant species. They developed and analyzed a nonlinear mathematical model that studies the dynamic of population density dependent emission of carbon dioxide in the atmosphere [10]. The model is governed by three nonlinearly dependent variables: Plant biomass density, population density and concentration of carbon dioxide. Using the method of stability theory of ordinary differential equation and numerical simulation, the result shows that the density of the plant biomass increase as the concentration of the carbon dioxide increases. It was also shown that the density of the plant biomass decreases as human population increases but the concentration of carbon dioxide increases in the atmosphere. Numerical simulation was used to confirm the analytical results [11].

In their research work on a model for interaction between forestry biomass, wildlife population and industrialization pressure, where the functional responses are assumed to be ratio-dependent showed that in the absence of industrialization. The density of the biomass and wildlife species are high and reduce when industrialization increases. The model encourages minimum green cover to be maintained with controlled expansion of industrial development ta sustain wildlife. The logistic models with prey-predator type nonlinear interaction terms to propose and analyze the depletion of forest resources caused by population and the corresponding population pressure. They assumed that the cumulative density of forestry resources and the density of the population follow logistic model. The model shows that carrying capacity of the forest resources decreases by population pressure. The model also shows that as the density of the forestry resources increases, the cumulative density of forestry resources decreases and the resources may go into extinct if population pressure becomes too large. The simulation analysis of the model confirms the analytic results. They proposed and analyzed a nonlinear mathematical model to access the effect of economic efforts applied to control population pressure and to increase forestry resources by the conservation of the forestry resources. Numerical simulation was also conducted to support the analytical results [12,13].

They proposed and analyzed a nonlinear mathematical model to study the simultaneous effects of industrialization, population and pollution on the depletion of a forestry resources biomass. Here the stability, global stability and instability are also obtained. The result shows that an increment in the population, pollution and industrialization decreases the forestry resource biomass and if no control measure is implemented, the forestry biomass may go into extinction. Computer simulation was also used to illustrate the results. In their paper attempted to assess the depletion of forestry resources biomass with population density and industrialization using the system of nonlinear differential equation. It was proven that forestry resources biomass reduces with increase in population and industrialization. The analytical results were confirmed by using the numerical simulation. The asymptotic method of differential equation was used to analyze the model [14,15].

Case Presentation of the Model

Shyam formulated a dynamical non-linear system of first order ordinary differential equation model that shows the effect of population and population augmented industrialization on forestry resources. Their assumptions here were that the Population density N(t), the Biomass density B(t) and the density of industrialization I(t) grow logistically and the forest biomass are been used by human beings to fulfil their needs. The model is as shown below:

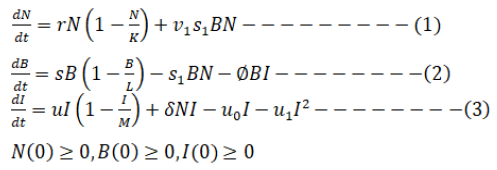
S₁: The depletion rate coefficient of forestry resources due to population growth and it is positive

V1: The cumulative growth rate of population and it is positive

∅: The depletion rate coefficient of forestry resources due to industrialization and it is positive

Δ: The growth rate coefficient of the industrialization due to population and it is positive

u1: The depletion rate coefficient due to crowding effect and it is positive

u0: The natural depletion rate coefficient of industrialization and it is positive

r: The intrinsic growth rate of N

s: The intrinsic growth rate of B

u: The intrinsic growth rate of I

K: The carrying capacity for N

L: The carrying capacity for B

M: The carrying capacity for I

Results and Discussion

Following researcher, we have utilized the following parameter values r=1, K=1000, v1=2, s1=0.0001, s=1.2, L=1500, ∅=0.0005, u=0.1, M=10, δ=0.0003, u0=0.01, u1=0.02. The values of N(t), B(t) and I(t) at equilibrium point are give as 1027, 1363 and 13 respectively.

We have utilized the application of ODE 45 which is computationally more efficient than other numerical methods like ODE 23, ODE 23tb ODE 155 etc (Table 1).

Conclusion

It is concluded that here has shown that if the population is maintained either above or at the equilibrium but not a little below equilibrium, varying the depletion rate of the forestry resources will not really affect the existence of the forestry resources but a little lower, the system will be unstable.

The forest must be regenerated at every given time to maintain the equilibrium so that the effect will not be noticed even as the human activity increases.

As we can see from the ODE 45, reduction in the equilibrium population makes the system unstable in the next paper.

References

1. Loreau, Michel, Shahid Naeem, Pablo Inchausti, and Jan Bengtsson, et al. "Biodiversity and Ecosystem Functioning: Current Knowledge and Future Challenges." Science 294 (2001): 804-808.

Google Scholar, Crossref

2. Hooper, David U, F Stuart Chapin III, John J Ewel, and Andrew Hector, et al. "Effects of Biodiversity on Ecosystem Functioning: A Consensus of Current Knowledge." Ecol Monogr 75 (2005): 3-35.

Google Scholar, Crossref

3. Cardinale, Bradley J., Emmett Duffy J., Andrew Gonzalez and David U Hooper, et al. "Biodiversity Loss and its Impact on Humanity." Nature 486 (2012): 59-67.

Google Scholar, Crossref

4. Nwagrabe, Eke, and Atsu J.U. "Modelling the Effects of Decreasing the Inter- Competition Coefficients on Biodiversity Loss." Int J Adv Eng Manag Sci 4 (2018): 239954.

Google Scholar, Crossref

5. Dubey, B. and Narayanan A. S. "Modelling Effects of Industrialization, Population and Pollution on a Renewable Resource." Nonlinear Analy Real World Applicat 11 (2010): 2833-2848.

Google Scholar, Crossref

6. Dubey, B., Upadhyay R.K. and Hussain J. "Effects of Industrialization and Pollution on Resource Biomass: A Mathematical Model." Ecol Model 167 (2003): 83-95.

Google Scholar, Crossref

7. Shukla, J.B, and Dubey B. "Modelling the Depletion and Conservation of Forestry Resources: Effects of Population and Pollution." J Math Biol 36 (1997): 71-94.

Google Scholar, Crossref

8. Shukla, J.B, Dubey B. and Freedman H. I. "Effect of Changing Habitat on Survival of Species." Ecol Model 87 (1996): 205-216.

Google Scholar, Crossref

9. Misra, A. K. and Kusum Lata. "Depletion and Conservation of Forestry Resources: A Mathematical Model." Different Equat Dynam Syst 23 (2015): 25-41.

Google Scholar, Crossref

10. Repetto, Robert, and Thomas Holmes. "The Role of Population in Resource Depletion in Developing Countries." Populat Deve Rev (1983): 609-632.

Google Scholar, Crossref

11. Tandon, Abhinav and Kumari Jyotsna. "A mathematical Model to Study the Simultaneous Effect of Pollutants Emitted from Wood and Non-Wood Based Industries on Forest Resources." World J Model Simul 12 (2016): 34-47.

Google Scholar

12. Shukla, J.B., Shyam Sundar, Shivangi and Ram Naresh. "Modeling and Analysis of the Acid Rain Formation due to Precipitation and its Effect on Plant Species." Nat Resour Model 26 (2013): 53-65.

Google Scholar

13. Sundar, Shyam. "Modeling and Analysis of the Survival of a Biological Species in a Polluted Environment: Effect of Environmental Tax." Comput Ecol Software 5 (2015): 201.

Google Scholar

14. Sundar, Shyam. "Effect of Elevated Carbon Dioxide Concentration on Plant Growth: A Mathematical Model." Am J Appl Math Stat 3 (2015): 59-67.

Google Scholar

15. Agarwal, Manju, Tazeen Fatima and Freedman H.I. "Depletion of Forestry Resource Biomass due to Industrialization Pressure: A Ratio-Dependent Mathematical Model." J Biol Dynam 4 (2010): 381-396.

Google Scholar, Crossref