Mini Review - (2022) Volume 11, Issue 6
Received: 05-Jun-2022, Manuscript No. JACM-21-001;
Editor assigned: 07-Jun-2022, Pre QC No. P-001;
Reviewed: 21-Jun-2022, QC No. Q-001;
Revised: 23-Jun-2022, Manuscript No. R-001;
Published:
30-Jun-2022
, DOI: 10.37421/2168-9679.22.11.478
Citation: Sati, Monika and Kailash Petwal . "Evolution of Electric and Magnetic Parts of Weyl Tensor in a Space-time." J Appl Computat Math 11(2022):478.
Copyright: © 2022 Sati M, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
The present paper is intended to study of the evolution of Electric and Magnetic parts of Weyl tensor in a space-time; in particular to measure the components of parts of Weyl tensor of an observer with a time-like 4-unit vector we have attempted to describe the tensors, which are the parts of Weyl tensor concerning for to the observeru. Further, we have established that if eigenvalues of any matrix are zero, real and imaginary then it is a part of Weyl tensor. Afterward, the cases from Petrov types have been obtained therein.
Curvature tensor • Ricci tensor • Space-time • Weyl tensor
Two gravitational quantities E and B which are Electric and Magnetic Weyl tensor connected to an observer u and playing an important role related to Electric and Magnetic fields. Some categories of the space-time can be detected by influencing the reality of an observer, for which, some limit of space-time are completed by the Weyl tensor electric and magnetic parts. Those properties have been applied to Weyl fields of electric and mag- netic parts, this is perfect integrability and very restrictive [1-3]. Thus, while a lot of physically attractive purely electric (E=0) solutions are known and magnetic (B=0) type D Weyl tensors with magnetized solutions may have valuable limitations.
From a famous insight, Einstein has already come up with the relativity that the different parts of Electric and Magnetic Weyl field on Maxwell’s Electromagnetism are strictly a unified thing, also the parts of Weyl tensor are relative to the maxwell tensor which is relative to the observer.
Conversely, Maxwell tensor Fij looking at any observer u and divided into its electric and magnetic parts relative to an observer u, the parts of Weyl tensor were presented by Matte and discovered the electric and magnetic gravitational units, which was playing an important role corresponding to electric and magnetic fields and was connected to any observer. They showed that these tensors satisfy the Maxwell equations for high- frequency gravitational waves and commented on the similarity between electromagnetism and gravitational fields [4-9].
Trumper studied that the curvature tensor of electric and magnetic parts is also an electric and observer u is an eigenvector of the Ricci tensor can be combined with an observer, which fully accepts the gravitational field as an observer with electric curvature. He showed that the weyl tensor is also an electric and u is an eigenvector of the Ricci tensor. Strictly, all known solutions of all gravitational fields and Einstein equa- tions such as correct foe example class of fluid Barnes, have an electric Weyl tensor. In the study of McIntosh et al, Weyl tensor of electric and Weyl tensor of magnetic in space-time are well-read descriptions is also given in durations of some Weyl scalar invariants. S must be real and infinite positive [10-12].
Preliminaries
The four rank tensor like Weyl tensor is defined as [6].
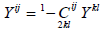 (1)
(1)
Now, consider the problem of finding eigenvalues λ and eigenvectors Yij as
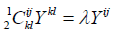 (2)
(2)
The Weyl tensors can have at most four linearly dependent eigenvectors. These eigenvectors are linked with few null vectors on the space-time, these are called the principal null directions [7]. The relevant multilinear algebra is somewhat involved, but the issued assortment theorem statement is there are possibly six types of algebraic symmetry, which is known as the Petrov types [13]. These Petrov type are as under:
(a) Type I: four simple principal null directions.
(b) Type II: One double and two simple principal null directions.
(c) Type III: One triple and one simple principal null directions.
(d) Type N: One quadruple principal null directions.
(d) Type D: Two double principal null directions.
(e) Type O: Vanishes Weyl tensor.
Now we use the Newmann- Penrose equations and the Weyl tensor as;
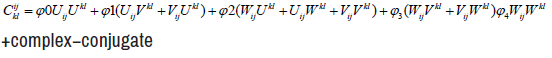 (3)
(3)
where φi are the scalars of Weyl tensor and the complex conjugate is denoted by c.c.
The six different Petrov types are distinguished by which of the Weyl scalars vanish. The following conditions are:
(a) Type I: φ0 = 0
(b) Type II: φ0 = φ1 = 0
(c) Type III: φ0 = φ1 = φ2 = 0
(d) Type D: φ0 = φ1 = φ3 = φ4 = 0
(e) Type N: φ0 = φ1 = φ2 = φ3 = 0
(f) Type O: φ0 = φ1 = φ2 = φ3 = φ4 = 0
Electric and magnetic parts of Weyl tensor
See an observer u with time like 4-unit u vector, such as an observer u is said to measure the components of electric and magnetic j parts +Ci
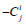 respectively, of the Weyl tensor by
respectively, of the Weyl tensor by
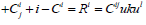 (4)
(4)
Where 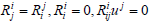 (5)
(5)
and 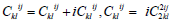 (6)
(6)
Here 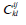 is are the Weyl tensor components
is are the Weyl tensor components
Theorem 2.1 The tensor  is parts of Weyl tensor concerning for to u if;
is parts of Weyl tensor concerning for to u if;

Proof: Let by the definitions of the orthogonal projector
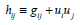 (7)
(7)
Define the tensor
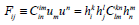 (8)
(8)
which is a rank 2 symmetric tensor of trace free this is moreover electric and magnetic parts which are locally relative to u Now, from eq (7), we solve fourth rank tensor as below:
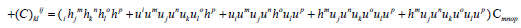 (9)
(9)
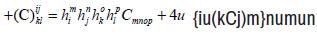 (10)
(10)
Now applying the property for parts of Weyl tensor from (Bel- Debever criteria)
Let u be a unit timelike vector,
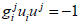 (11)
(11)
then Weyl tensor  is electric and magnetic concerning for
to a unit time like vector u iff i.e.
is electric and magnetic concerning for
to a unit time like vector u iff i.e.
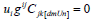 (12)
(12)
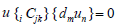 (13)
(13)
Hence  is electric and magnetic part of Weyl tensor.
Corollary: The tensor is said to be electric iff the Weyl tensor is electric i.e
is electric and magnetic part of Weyl tensor.
Corollary: The tensor is said to be electric iff the Weyl tensor is electric i.e
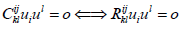 (14)
(14)
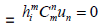 (15)
(15)
Where 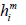 is the projection tensor defined as
is the projection tensor defined as 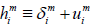 (16)
(16)
Remark: The vaccum matrix is an example of electric Weyl ten- sors and the electric Weyl tensor have been discussed in a spacetime with cosmological models of inhomogeneous.
Corollary: The tensor is said to be magnetic iff the Weyl tensor is magnetic.
Remark: The non-vaccume matrix is an example magnetic Weyl tensor.
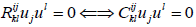 (17)
(17)
Theorem 2.2 If the eigenvalues of any matrix A in spacetime is zero, purely real and purely imaginary then the Weyl tensor is electric and magnetic.
Here is a brief discussion on some main outcomes of this article written in favor of the evolution of electric and magnetic parts of the Weyl tensor in a spacetime.
The introductory and preliminary section gives the details about the basic concept of electric and magnetic parts of Weyl tensor connected to an observer u and playing a role related to their fields. The Petrov types definitions are explained in the preliminaries and −(C)i of the Weyl tensor in terms of an observer with time like 4-unit vector, also consider a matrix, which has ten real numbers corresponding to ten independent complex Newmann-Penrose components of Weyl tensor, with the help of these considerations we investigate the conditions that two tensors are said to be an electric and magnetic part of the Weyl tensors. Also, study the properties of Weyl tensors for considerating some eigenval- ues of the matrix and afterward arises some corollaries and important cases related to them.
Journal of Applied & Computational Mathematics received 1282 citations as per Google Scholar report